详解Graph Embedding经典方法：算法原理、代码实现与应用样例

导读

我们都知道在数据结构中，图是一种基础且常用的结构。现实世界中许多场景可以抽象为一种图结构，如社交网络，交通网络，电商网站中用户与物品的关系等。以躺平APP社区为例，它是“躺平”这个大生态中生活方式分享社区，分享生活分享家，努力打造社区交流、好物推荐与居家指南。用户在社区的所有行为：发布、点击、点赞、评论收藏等都可以抽象为网络关系图。因此Graph Embedding技术非常自然地成为学习社区中用户与内容的embedding的一项关键技术。

目前落地的模型大致两类：直接优化节点的浅层网络模型和基于GNN的深层网络模型。前者包括基于用户行为理解内容，学习内容向量表征的item2vec,用于扩充i2i召回；同时学习用户与内容向量表征的异构网络表示学习模型metapath2vec，用于提高内容召回的多样性；以群体行为代替个体行为的userCluster2vec，缓解新用户冷启动问题。后者包括采用邻域聚合的思想，同时融入节点属性信息，通过多层节点聚合使得网络中的拓扑结构能够有效捕捕获的graphSage，以及将attention机制运用邻域信息聚合阶段的GAT，对用户与内容向量表征进行更加细致化学习。

这里先看下 Graph Embedding 的相关内容。

Graph Embedding 技术将图中的节点以低维稠密向量的形式进行表达，要求在原始图中相似 ( 不同的方法对相似的定义不同 ) 的节点其在低维表达空间也接近。得到的表达向量可以用来进行下游任务，如节点分类，链接预测，可视化或重构原始图等。

DeepWalk

虽然 DeepWalk 是 KDD 2014的工作，但却是我们了解 Graph Embedding 无法绕过的一个方法。

我们都知道在 NLP 任务中，word2vec 是一种常用的 word embedding 方法， word2vec 通过语料库中的句子序列来描述词与词的共现关系，进而学习到词语的向量表示。

DeepWalk 的思想类似 word2vec，使用图中节点与节点的共现关系来学习节点的向量表示。那么关键的问题就是如何来描述节点与节点的共现关系，DeepWalk 给出的方法是使用随机游走 (RandomWalk) 的方式在图中进行节点采样。

RandomWalk 是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点，从其邻居中随机采样节点作为下一个访问节点，重复此过程，直到访问序列长度满足预设条件。

获取足够数量的节点访问序列后，使用 skip-gram model 进行向量学习。

▐ DeepWalk 核心代码

DeepWalk 算法主要包括两个步骤，第一步为随机游走采样节点序列，第二步为使用 skip-gram modelword2vec 学习表达向量。

• 构建同构网络，从网络中的每个节点开始分别进行 Random Walk 采样，得到局部相关联的训练数据
• 对采样数据进行 SkipGram 训练，将离散的网络节点表示成向量化，最大化节点共现，使用 Hierarchical Softmax 来做超大规模分类的分类器

▐ Random Walk

我们可以通过并行的方式加速路径采样，在采用多进程进行加速时，相比于开一个进程池让每次外层循环启动一个进程，我们采用固定为每个进程分配指定数量的num_walks的方式，这样可以最大限度减少进程频繁创建与销毁的时间开销。

deepwalk_walk方法对应上一节伪代码中第6行，_simulate_walks对应伪代码中第3行开始的外层循环。最后的Parallel为多进程并行时的任务分配操作。

def deepwalk_walk(self, walk_length, start_node):

    walk = [start_node]

    while len(walk) < walk_length:
        cur = walk[-1]
        cur_nbrs = list(self.G.neighbors(cur))
        if len(cur_nbrs) > 0:
            walk.append(random.choice(cur_nbrs))
        else:
            break
    return walk

def _simulate_walks(self, nodes, num_walks, walk_length,):
    walks = []
    for _ in range(num_walks):
        random.shuffle(nodes)
        for v in nodes:           
            walks.append(self.deepwalk_walk(alk_length=walk_length, start_node=v))
    return walks

results = Parallel(n_jobs=workers, verbose=verbose, )(
    delayed(self._simulate_walks)(nodes, num, walk_length) for num in
    partition_num(num_walks, workers))

walks = list(itertools.chain(*results))

▐ Word2vec

这里就偷个懒直接用gensim里的 Word2Vec 了。

from gensim.models import Word2Vec
w2v_model = Word2Vec(walks,sg=1,hs=1)

▐ DeepWalk 应用

这里简单的用 DeepWalk 算法在 wiki 数据集上进行节点分类任务和可视化任务。 wiki 数据集包含 2,405 个网页和17,981条网页之间的链接关系，以及每个网页的所属类别。

本例中的训练，评测和可视化的完整代码在下面的 git 仓库中：

https://github.com/shenweichen/GraphEmbedding

G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])

model = DeepWalk(G,walk_length=10,num_walks=80,workers=1)
model.train(window_size=5,iter=3)
embeddings = model.get_embeddings()

evaluate_embeddings(embeddings)
plot_embeddings(embeddings)

▐ 分类任务结果

micro-F1 : 0.6674
macro-F1 : 0.5768

▐ 可视化结果

LINE

之前介绍过DeepWalk，DeepWalk使用DFS随机游走在图中进行节点采样，使用word2vec在采样的序列学习图中节点的向量表示。

LINE也是一种基于邻域相似假设的方法，只不过与DeepWalk使用DFS构造邻域不同的是，LINE可以看作是一种使用BFS构造邻域的算法。此外，LINE还可以应用在带权图中(DeepWalk仅能用于无权图)。

之前还提到不同的graph embedding方法的一个主要区别是对图中顶点之间的相似度的定义不同，所以先看一下LINE对于相似度的定义。

▐ LINE 算法原理

1. 一种新的相似度定义

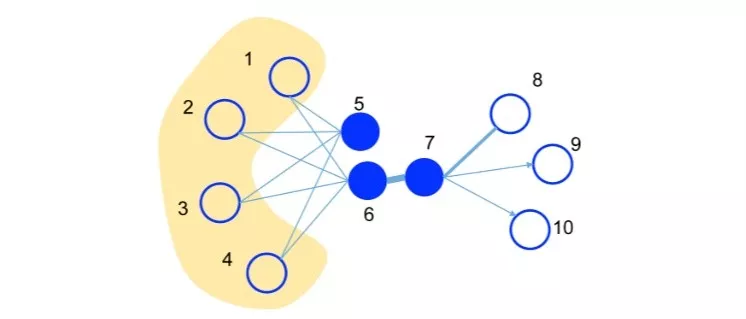
✎ first-order proximity

1阶相似度用于描述图中成对顶点之间的局部相似度，形式化描述为若之间存在直连边，则边权即为两个顶点的相似度，若不存在直连边，则1阶相似度为0。如上图，6和7之间存在直连边，且边权较大，则认为两者相似且1阶相似度较高，而5和6之间不存在直连边，则两者间1阶相似度为0。

✎ second-order proximity

仅有1阶相似度就够了吗？显然不够，如上图，虽然5和6之间不存在直连边，但是他们有很多相同的邻居顶点(1,2,3,4)，这其实也可以表明5和6是相似的，而2阶相似度就是用来描述这种关系的。形式化定义为，令表示顶点与所有其他顶点间的1阶相似度，则与的2阶相似度可以通过和的相似度表示。若与之间不存在相同的邻居顶点，则2阶相似度为0。

2. 优化目标

✎ 1st-order

对于每一条无向边（i，j），定义顶点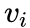和之间的联合概率为：，为顶点的低维向量表示。（可以看作一个内积模型，计算两个item之间的匹配程度）

同时定义经验分布：

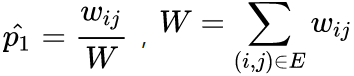
优化目标为最小化：

是两个分布的距离，常用的衡量两个概率分布差异的指标为KL散度，使用KL散度并忽略常数项后有：

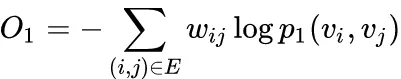
1st order 相似度只能用于无向图当中。

✎ 2nd-order
这里对于每个顶点维护两个embedding向量，一个是该顶点本身的表示向量，一个是该点作为其他顶点的上下文顶点时的表示向量。

对于有向边（i，j），定义给定顶点条件下，产生上下文(邻居)顶点的概率为：，其中为上下文顶点的个数。

优化目标为：

，其中为控制节点重要性的因子，可以通过顶点的度数或者PageRank等方法估计得到。

经验分布定义为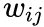：，是边（i，j）的边权，是顶点的出度，对于带权图，
使用KL散度并设，忽略常数项，有

**3. 优化技巧

**

✎ Negative sampling
由于计算2阶相似度时，softmax函数的分母计算需要遍历所有顶点，这是非常低效的，论文采用了负采样优化的技巧，目标函数变为：

，k是负边的个数。
论文使用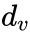，是顶点的v出度。

✎ Edge Sampling

注意到我们的目标函数在log之前还有一个权重系数，在使用梯度下降方法优化参数时，会直接乘在梯度上。如果图中的边权方差很大，则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸，较小的学习率对于较小的边权则会导致梯度过小。

对于上述问题，如果所有边权相同，那么选择一个合适的学习率会变得容易。这里采用了将带权边拆分为等权边的一种方法，假如一个权重为w的边，则拆分后为w个权重为1的边。这样可以解决学习率选择的问题，但是由于边数的增长，存储的需求也会增加。

另一种方法则是从原始的带权边中进行采样，每条边被采样的概率正比于原始图中边的权重，这样既解决了学习率的问题，又没有带来过多的存储开销。
这里的采样算法使用的是Alias算法，Alias是一种时间复杂度的离散事件抽样算法。具体内容可以参考：

Alias Method:时间复杂度O(1)的离散采样方法

https://zhuanlan.zhihu.com/p/54867139

4. 其他问题

✎ 低度数顶点
对于一些顶点由于其邻接点非常少会导致embedding向量的学习不充分，论文提到可以利用邻居的邻居构造样本进行学习，这里也暴露出LINE方法仅考虑一阶和二阶相似性，对高阶信息的利用不足。

✎ 新加入顶点
对于新加入图的顶点，若该顶点与图中顶点存在边相连，我们只需要固定模型的其他参数，优化如下两个目标之一即可：

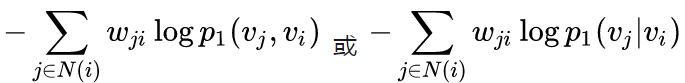
若不存在边相连，则需要利用一些side info，留到后续工作研究。

▐ LINE核心代码

1. 模型和损失函数定义

LINE使用梯度下降的方法进行优化，直接使用tensorflow进行实现，就可以不用人工写参数更新的逻辑了~

这里的 实现中把1阶和2阶的方法融合到一起了，可以通过超参数order控制是分开优化还是联合优化，论文推荐分开优化。

首先输入就是两个顶点的编号，然后分别拿到各自对应的embedding向量，最后输出内积的结果。真实label定义为1或者-1，通过模型输出的内积和line_loss就可以优化使用了负采样技巧的目标函数了~

def line_loss(y_true, y_pred):
    return -K.mean(K.log(K.sigmoid(y_true*y_pred)))def create_model(numNodes, embedding_size, order='second'):

    v_i = Input(shape=(1,))
    v_j = Input(shape=(1,))

    first_emb = Embedding(numNodes, embedding_size, name='first_emb')
    second_emb = Embedding(numNodes, embedding_size, name='second_emb')
    context_emb = Embedding(numNodes, embedding_size, name='context_emb')

    v_i_emb = first_emb(v_i)
    v_j_emb = first_emb(v_j)

    v_i_emb_second = second_emb(v_i)
    v_j_context_emb = context_emb(v_j)

    first = Lambda(lambda x: tf.reduce_sum(
        x[0]*x[1], axis=-1, keep_dims=False), name='first_order')([v_i_emb, v_j_emb])
    second = Lambda(lambda x: tf.reduce_sum(
        x[0]*x[1], axis=-1, keep_dims=False), name='second_order')([v_i_emb_second, v_j_context_emb])

    if order == 'first':
        output_list = [first]
    elif order == 'second':
        output_list = [second]
    else:
        output_list = [first, second]

    model = Model(inputs=[v_i, v_j], outputs=output_list)

2. 顶点负采样和边采样

下面的函数功能是创建顶点负采样和边采样需要的采样表。中规中矩，主要就是做一些预处理，然后创建alias算法需要的两个表。

def _gen_sampling_table(self):

    # create sampling table for vertex
    power = 0.75
    numNodes = self.node_size
    node_degree = np.zeros(numNodes)  # out degree
    node2idx = self.node2idx

    for edge in self.graph.edges():
        node_degree[node2idx[edge[0]]
                    ] += self.graph[edge[0]][edge[1]].get('weight', 1.0)

    total_sum = sum([math.pow(node_degree[i], power)
                        for i in range(numNodes)])
    norm_prob = [float(math