卷积神经网络基础

全连接层：输入层，隐藏层，输出层

卷积层

卷积目的：进行图像特征提取

卷积特性：1.拥有局部感知机制（因为以一个滑动窗口的形式在滑动计算，所以是有局部感知能力的）

                    2.权值共享（因为在滑动的过程中，它的值是不会发生变化的，所以具有权值共享特性）

1.卷积核的深度与输入特征层的深度相同

2.输出的特征矩阵深度与卷积核的个数相同

加入偏移量bias:

输出特征矩阵的每一个元素与偏移量相加

加上激活函数：引入非线性因素，使其具备解决非线性问题的能力

激活函数的作用和原理

激活函数的主要作用是提供网络的非线性建模能力。在卷积层中，我们主要采用了卷积的方式来处理，也就是对每个像素点赋予一个权值，这个操作显然就是线性的。但是对于我们样本来说，不一定是线性可分的，为了解决这个问题，我们可以进行线性变化，或者我们引入非线性因素，解决线性模型所不能解决的问题。如果没有激活函数，那么该网络仅能够表达线性映射，此时即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。因此也可以认为，只有加入了激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。

常用的激活函数：sigmoid,Relu

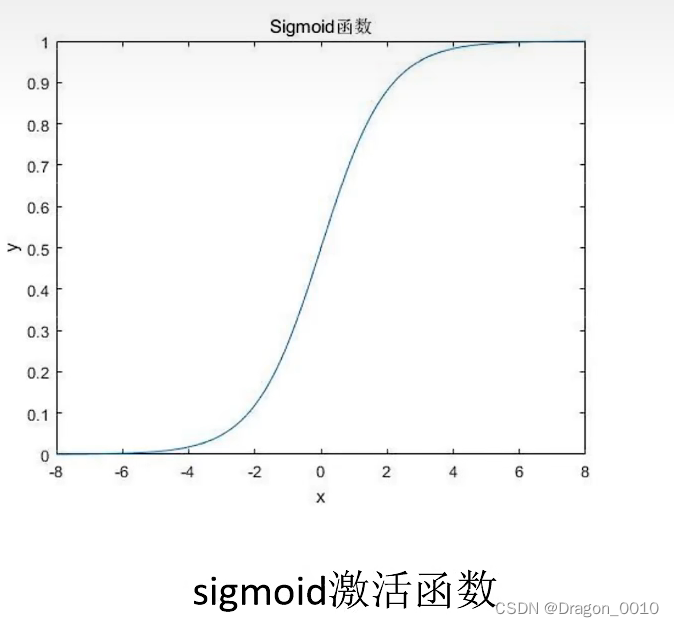
 sigmoid激活函数饱和时梯度值非常小（当x的值越来越大的时候，它的导数趋近于0，增长的很小很小），故网络层数较深时容易出现梯度消失（本质是因为链式法则的乘法特性导致的），对于sigmoid，导数的最大值在输入为0处时，值为0.25，考虑一个多层神经网络，则梯度向后传导时，每经过一个sigmoid都需要乘以一个小于0.25的梯度，梯度的衰减会非常的大，迅速接近0

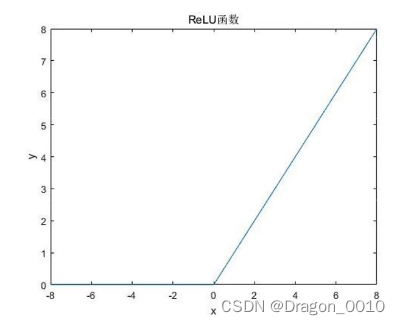
Relu激活函数 x小于0时，函数结果全为0，x大于0时，函数结果为x。

缺点在于当反向传播过程中有一个非常大的梯度经过时，反向传播更新后可能导致权重分布中心小于0，导致该处的导数始终为0，反向传播无法更新权重，即进入失活状态。

在卷积操作过程中，矩阵经卷积操作后的尺寸由以下几个因数决定：

1.输入图片大小W×W

2.Filter（滤波器、卷积核）的大小

3.步长S

4.padding（在滑动窗口时，不足的地方补0）的像素P

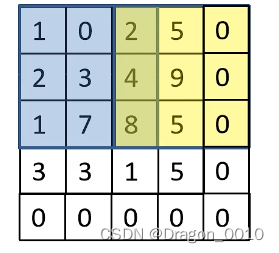
 图片大小4*4  卷积核大小3*3  步长为2   padding这个只在右边和下边补0 所以只加一个p 

正常情况下是对称的，要+2p

经过卷积后的矩阵尺寸大小计算公式为：

N = (W - F +2P)/S+1

N=(4-3+1)/2+1=2

池化层

池化层目的：对特征图进行稀疏处理，减少数据运算

MaxPooling 最大下采样层

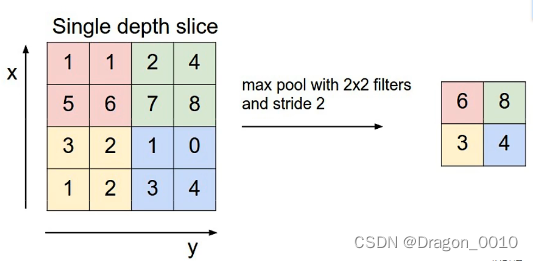
 2*2大小的池化核为例做最大下采样操作

AveragePooling平均下采样层

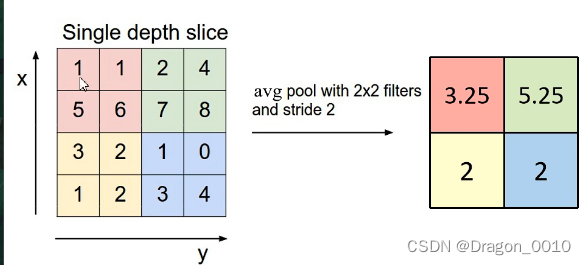
池化层特点：

1.没有训练参数

2.只改变特征矩阵的宽度和高度，并不会改变深度 比如说从4*4*3，经过池化过后变成2*2*3

3.一般池化核的尺寸与步长相同

误差的计算

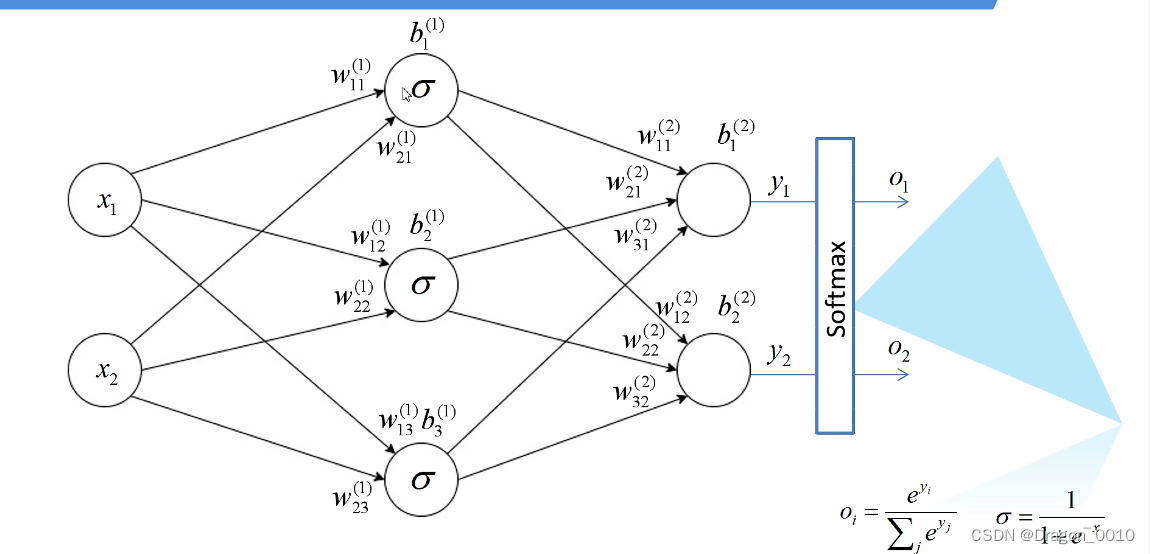
 输入层：X1 X2

中间的是隐藏层：设置了3个节点  σ代表的是激活函数

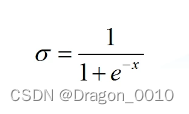
输出

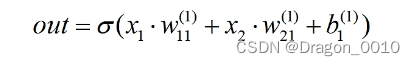
经过softmax处理后所有输出节点概率和为1

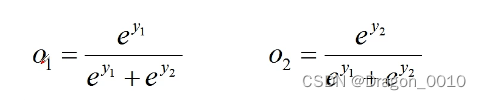
 Cross Entropy Loss 交叉熵损失

1.针对多分类问题（Softmax输出，所有输出概率和为1）

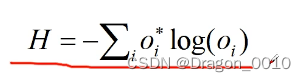
 2.针对二分类问题（sigmoid输出，每个输出节点之间互不相干）

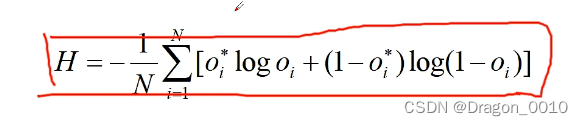
 误差的反向传播

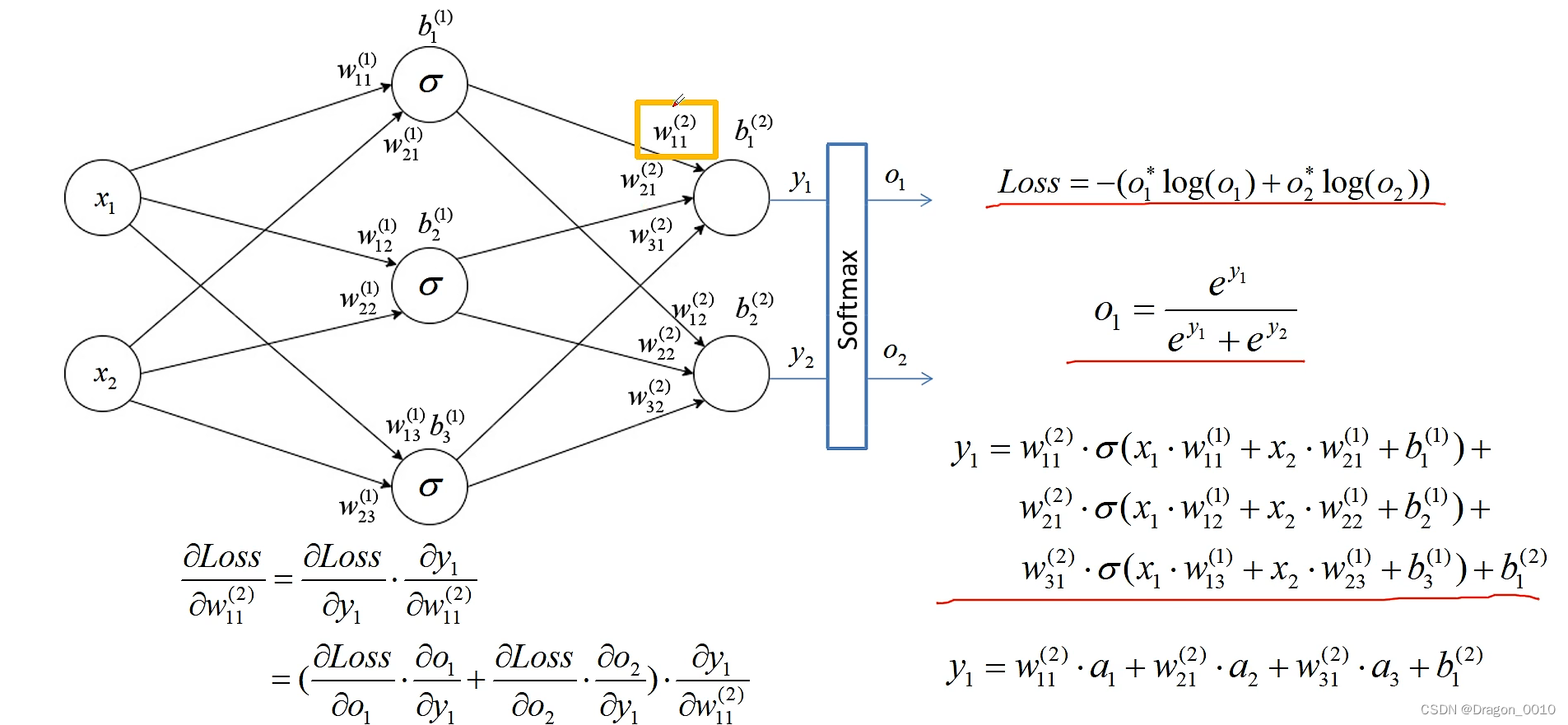
权重的更新（gradient 梯度）

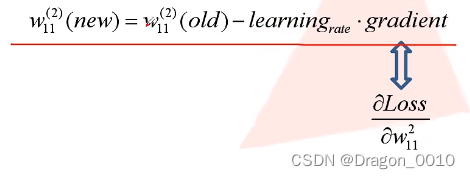
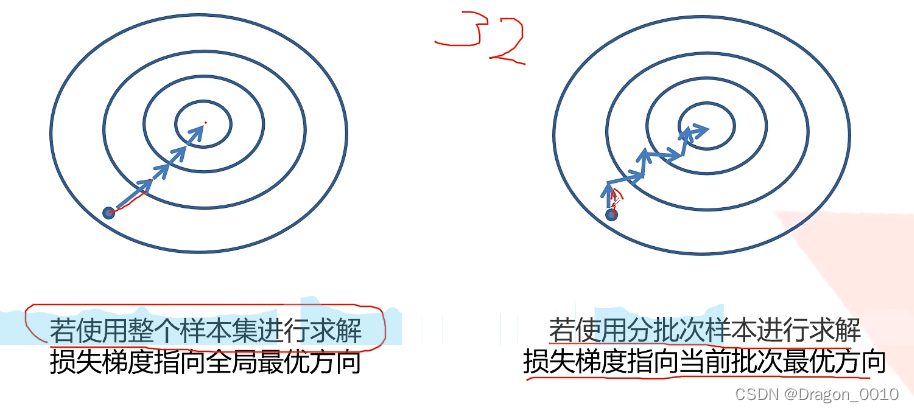
如果用整个样本集进行求解，损失梯度的方向全局最优的方向，损失减少最快的方向

如果分批次样本进行求解，损失梯度指向当前批次最优方向

 优化器（optimazer）

作用：使网络得到更快的收敛

SGD优化器

 噪声（样本存在一些误差，可能有些样本的标注是错误的）

 有效化解样本噪声的干扰