NumPy(Numerical Python)是Python科学计算的基石,提供高性能多维数组对象ndarray及数学运算函数库。其核心优势在于:
- 高效存储:同类型数据连续存储,减少内存占用。
- 向量化运算:无需显式循环即可完成批量操作。
- 广播机制:支持不同形状数组间的自动扩展计算。
一、NumPy库的安装
使用pip安装Nunpy库的安装命令代码如下所示:
#pip方式安装Numpy库
#默认安装最新版本
pip install numpy
#安装指定的版本
pip install numpy==1.18.5
#使用国内镜像源进行安装
pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple目前国内常用的一些Python第三方库镜像源如下所示:
- 清华大学镜像源:https://pypi.tuna.tsinghua.edu.cn/simple/。
- 阿里云镜像源:Simple Index。
- 华为云镜像源:https://mirrors.huaweicloud.com/repository/pypi/simple/。
- 网易镜像源:https://mirrors.163.com/pypi/simple/。
- 豆瓣镜像源:https://pypi.douban.com/simple/。
- 百度云镜像源:https://mirror.baidu.com/pypi/simple/。
- 中国科技大学镜像源:Verifying - USTC Mirrors。
二、列表与数组的区别
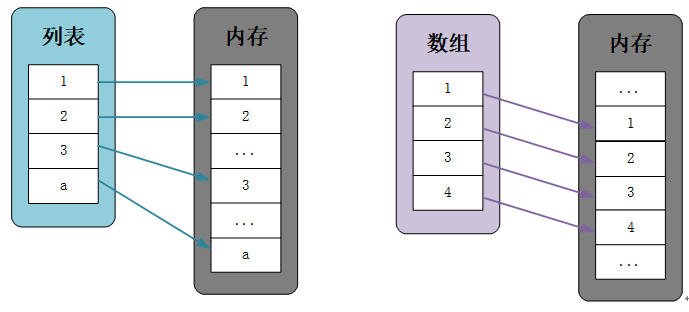
Numpy模块最重要的特征是ndarray对象,是一个N维数组。数组的概念在C++、Java等编程语言中存在,但是在Python内置的数据类型中没有数组这种对象,不过存在一个比较相似的列表对象。数组与列表的差异主要体现在以下几个方面:
- 列表中可以存放任意数据类型的元素。
- ndarray数组中仅能存放相同数据类型的元素。
- 列表在内存中占用的空间较大,因为需要为每个元素存储额外的信息(元素引用、元素类型等)。并且由于列表的灵活性,其内存分配不是连续的,会影响对元素的访问速度。
- ndarray对象由于所有元素类型相同,且内存分配连续,因此访问速度非常快。在内存中采用紧凑的存储方式,减少了内存占用。此外,ndarray底层使用C语言编写,进一步提高了运算性能(C语言是公认的运行效率最高的语言,大多数情况下需要较高运行效率的底层设计都是通过C语言编写的)。
- ndarray对象支持高效的元素级运算,包括与标量的运算和数组之间的矢量化运算。此外,ndarray还支持广播机制,允许不同维度的数组进行运算。
- 列表支持基本的元素级运算,但通常需要通过循环结构逐个处理元素,对于大规模数据处理效率较低。列表之间的“相加”操作实际上是连接两个列表,而非元素对元素的相加。
三、数组的构建
(1)numpy.array()方式创建数组:
# 导入numpy模块
import numpy as np
# 创建一个Python列表
py_list=[1,20,3,25,7,33]
# numpy.array()方式创建数组 将列表转化为数组
np_array=np.array(py_list)
print(f"这是一个Python列表,类型为{type(py_list)},列表为{py_list}")
print(f"这是一个ndarray数组,类型为{type(np_array)},数组为{np_array}")
(2)创建特殊值数组:
1.创建填充值全为0的数组
# 一维零数组
zeros_1d = np.zeros(5) # [0., 0., 0., 0., 0.]
# 二维零矩阵
zeros_2d = np.zeros((3, 4)) # 3行4列
# 指定数据类型
zeros_int = np.zeros(5, dtype=np.int32) # [0, 0, 0, 0, 0]# 填充特殊值2.创建填充值全为1的数组
# 一维全1数组
ones_1d = np.ones(4) # [1., 1., 1., 1.]
# 三维全1数组 (2x3x4)
ones_3d = np.ones((2, 3, 4))
3.创建填充特定值的数组
# 创建填充特定值的数组
full_arr = np.full((2, 3), 7) # 2x3数组填充7
# 结构为 [[7, 7, 7],[7, 7, 7]]
# 填充特殊值
nan_arr = np.full((3, 2), np.nan) # 填充NaN
inf_arr = np.full((2, 2), np.inf) # 填充正无穷3.创建单位矩阵
# 3x3单位矩阵
eye_matrix = np.eye(3)
# 结构为 [[1., 0., 0.],[0., 1., 0.],[0., 0., 1.]]
# 偏移对角线
eye_k = np.eye(4, k=1) # 主对角线向上偏移1位
# 输出 [[0., 1., 0., 0.],[0., 0., 1., 0.],[0., 0., 0., 1.],[0., 0., 0., 0.]]4.创建空数组
# 创建未初始化的数组(内容为内存中的随机值)
empty_arr = np.empty((2, 3))
# 可能输出:
# [[6.23042070e-307, 4.67296746e-307, 1.69121096e-306],
# [1.33511562e-306, 1.89146896e-307, 1.78022342e-306]]四、数组的切片与索引
(1)基础索引:
在对数组进行索引操作时,不同维度的数组所需的索引值数量是不同的。简单来讲,每个维度都需要一个对应的索引值来定位数组中的元素。
import numpy as np
# 创建一个一维数组
np_array_1d=np.arange(10)
# 一维数组索引
print(f"数组的正索引,数组{np_array_1d}中的第一个元素是:{np_array_1d[0]}")
print(f"数组的负索引,数组{np_array_1d}中的最后一个元素:{np_array_1d[-1]}")
# 一维数组的切片
# 通过[]方式进行数组的切片
print(f"普通[]方式进行数组的切片,数组{np_array_1d}的一个切片是:{np_array_1d[2:6:2]}")
# 通过内置的slice()函数创建切片对象
section=slice(2,8,2)
print(f"内置函数slice()函数方式进行数组切片,数组{np_array_1d}的一个切片是:{np_array_1d[section]}")
# 创建一个多维数组
multi_array_2d=np.array([[1,2,3],[4,5,6],[7,8,9]])
# 多维数组的索引:
print("___多维数组的索引操作___")
print(f"获取多维数组\n{multi_array_2d}\n中的单个子数组是:\n{multi_array_2d[0]}")
print(f"获取多维数组\n{multi_array_2d}\n中的第二个子数组中的第二个元素:\n{multi_array_2d[1,1]}")
print (f"获取多维数组\n{multi_array_2d}\n中的第二列的元素:\n{multi_array_2d[...,1]}") # 第2列元素
print (f"获取多维数组\n{multi_array_2d}\n中的第二行的元素:\n{multi_array_2d[1,...]}") # 第2行元素
# 多维数组的切片:
print("___多维数组的切片操作___")
# 获取多维数组中第一行与第二行中的第二列与第三列的子矩阵
print(f"获取多维数组\n{multi_array_2d}\n中的指定的子矩阵是:\n{multi_array_2d[0:2,1:]}")
# 获取多维数组中所有行的第一列与第二列的子矩阵
print(f"获取多维数组\n{multi_array_2d}\n中所有行的第二列与第三列的子矩阵:\n{multi_array_2d[:,1:]}")
# 获取第一行与第二行中的所有列的子矩阵
print (f"获取多维数组\n{multi_array_2d}\n中第一行与第二行的所有列的子矩阵:\n{multi_array_2d[:2,:]}")
# 获取所行的第一第二列的子矩阵
print (f"获取多维数组\n{multi_array_2d}\n中所有行的所有列的子矩阵:\n{multi_array_2d[...,:]}")(2)高级索引:
1.整数数组索引
# 整数数组索引
int_array_row=[0,1,2]
int_array_column=[0,1,2]
#获取数组中第一行第一列的元素、第二行第二列的元素、第三行第三列的元素
print(f"通过整数数组索引来访问数组\n{multi_array}\n的元素是
{multi_array[int_array_row,int_array_column]}")
2.花式索引
# 创建一个多维数组
multi_array=np.arange(32).reshape((8,4))#将数组转化为指定形状的数组
# 花式索引 获取第4,2,1,3行的数据
fancy_array=multi_array[[4,2,1,3]]
print(f"通过花式索引来访问数组\n{multi_array}\n的元素是\n{fancy_array}")
3.布尔索引
# 创建一个多维数组
multi_array=np.arange(12).reshape((3,4))#将数组转化为指定形状的数组
# 布尔索引 获取数组中大于5的元素
bool_array=multi_array[multi_array>5]
print(f"通过布尔索引来访问数组\n{multi_array}\n的元素是\n{bool_array}")
五、NumPy库的数组操作与广播机制
(1)数组拼接(Concatenation):
数组拼接的核心思想就是沿着指定的轴(axis)将多个数组连接起来。不同的拼接方向对应不同的axis参数,从而实现按行、按列、按深度等不同维度的组合。
在NumPy中数组的“维度”与“轴”(Axis)如下所示:
- 一维数组:shape = (n,) →轴axis=0
- 二维数组:shape = (m, n) → axis=0(行),axis=1(列)
- 三维数组:shape = (d, m, n) → axis=0(深度块),axis=1(行),axis=2(列)
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])
# 垂直拼接 沿 axis=0 拼接(垂直方向,增加行数)
v_stack = np.vstack([a, b])
# 输出 [[1 2][3 4][5 6]]
# 水平拼接 沿 axis=1 拼接(水平方向,增加列数)
h_stack = np.hstack([a, a])
# 输出 [[1 2 1 2][3 4 3 4]]
# 深度拼接 沿 axis=2 拼接(深度方向,增加“通道”或“层”)
d_stack = np.dstack([a, a])
# 输出 [[[1 1][2 2]][[3 3][4 4]]]
# 通用拼接
concat = np.concatenate([a, b], axis=0) # 同vstack(2)数组变形(Reshaping):
# 创建初始数组
arr = np.array([[1, 2, 3],[4, 5, 6]])
arr_reshaped = arr.reshape((3, 2))
print(arr_reshaped)
# [[1 2][3 4][5 6]]
# 使用 -1 自动推断维度
a.reshape((2, -1)) # → (2,3),-1 表示自动计算
a.reshape((-1,)) # 展平为一维 → (6,)
(3)数组转置(Transpose):
1.使用.T
.T是最简单的转置方式,适用于所有维度的数组,但默认情况下仅对二维数组有效(即简单地交换第一和第二轴)。
# 创建一个 2x3 矩阵
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a.T)
# 输出:
# [[1 4][2 5][3 6]]2.使用np.transpose()函数
np.transpose()提供了更灵活的方式进行转置操作,允许你指定新的维度顺序。
# 创建二维数组
a = np.array([[1, 2, 3], [4, 5, 6]])
transposed = np.transpose(a)
print(transposed)
# 创建一个 3D 数组 (2, 3, 4)
a_3d = np.arange(24).reshape((2, 3, 4))
print("Original shape:", a_3d.shape) # (2, 3, 4)
# 转置: 交换第一个和第三个维度
transposed_3d = np.transpose(a_3d, (2, 1, 0))
print("Transposed shape:", transposed_3d.shape) # (4, 3, 2)3.使用swapaxes()方法
np.swapaxes()方法用于交换两个特定的轴,这对于快速调整某些维度特别有用。
# 创建一个 3D 数组 (2, 3, 4)
a_3d = np.arange(24).reshape((2, 3, 4))
print("Original shape:", a_3d.shape) # (2, 3, 4)
swapped = np.swapaxes(a_3d, 0, 2)
print("Swapped axes shape:", swapped.shape) # (4, 3, 2)(4)广播机制
广播是NumPy中的一种强大机制,在进行数组间的操作时,可以自动适配不同形状的数组,实现数组之间元素级别的操作。这种机制的出现,可以避免循环操作与显示的扩展数组维度的冗长代码,使数组的操作更加方便,代码更加简洁;广播操作是在数组的内部完成的,要比普通的循环操作执行效率更高;广播可以在不改变原始数组形状的情况下,实行对数组更为复杂的操作,能够有效提升代码的灵活性。
广播的本质是说如果有a、b两个数组形状满足a.shape==b.shape,那么这两个数组进行元素级操作时,例如,a*b的操作结果就是a与b两个数组中对应位置的元素相乘(这里要求两个数组的维度相同,并且每个维度的长度相同)。出于这个限制,如果两个形状不同的数组进行广播操作时,会在自动进行形状的处理,是两个数组的形状保持一致,一般是将低纬度的数组,或者将维度中长度较短的数组进行拉伸至维度中长度最长的数组。
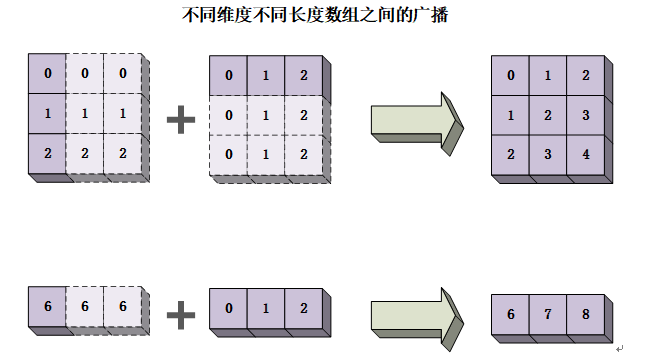
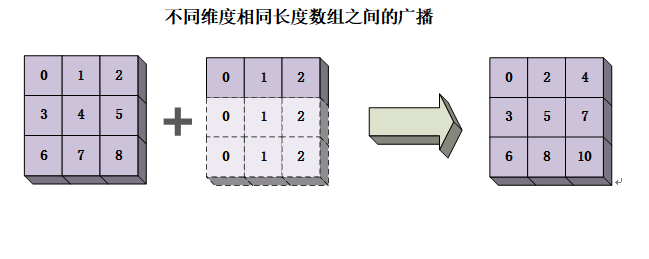
不同数组之间进行广播操作时需要满足以下规则:
- 不同数组进行广播时,所有数组都向其中形状最长的数组看齐,形状不足的部分都通过在前面(左侧)补1。例如,a数组是一个二维数组,其形状为a.shape=(3,3);b数组是一个一维数组,其形状为b.shape=(3),这两个数组进行广播操作(例如,a+b),就会按照形状最大的a数组,来补足b数组的形状,使b数组变成一个二维数组结构b.shape=(1,3),然后按照a数组中对应维度长度,来复制b数组保证在这一维度上长度保持一致。这里a数组中对应的维度是行其长度为3,则b数组需要复制的次数为3/1=3次。
- 如果两个数组的形状在任何维度上均不匹配,但是其中某一个数组中的某一维度为1,则该维度中形状为1的数组将被拉伸到与另一个数组对应维度的形状相匹配。例如,数组a的形状为a.shape=(3,1),数组b的形状为b.shape=(1,3),这两个数组进行广播操作时,数组a、b的形状会被分别拉伸为a.shape(3,3)与b.shape(3,3)。
- 如果两个数组的形状在任何维度上均不匹配,且均没有等于1的维度,那么这两个数组在进行广播操作时无法正确转换,会导致出错。





















 1649
1649

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








