还弄不懂机器学习里的正则化？2分钟生动图解带你一次搞清

什么是正则化

正则化（Regularization）是一种防止机器学习Model过拟合的技术；它通过在模型的损失函数中添加一个惩罚项的方式来约束模型的负载度。这个惩罚项一般而言是模型参数的某种范数（Norm），例如L1和L2范数。

范数

范数（Norm）是什么 范数是一个函数，赋予向量空间中的每个向量一个长度（或者说大小），简单来讲就是衡量向量长短或者大小的一种方法。

L1 vs L2 Norm

• L1正则化又称为LASSO、L1范数，是模型所有参数的绝对值和。
  
   

  

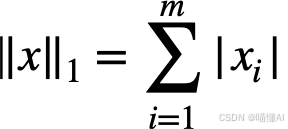
• L2正则化又称为Ridge岭回归，是模型所有参数平方和的平方根。
   

  

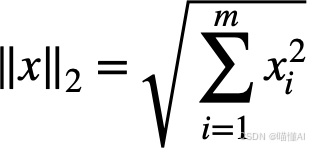
两种方法都有降低过拟合的效果。L1范数可以用于特征选择，但由于不可导，不能使用常规梯度下降法优化。而L2范数别于求导。

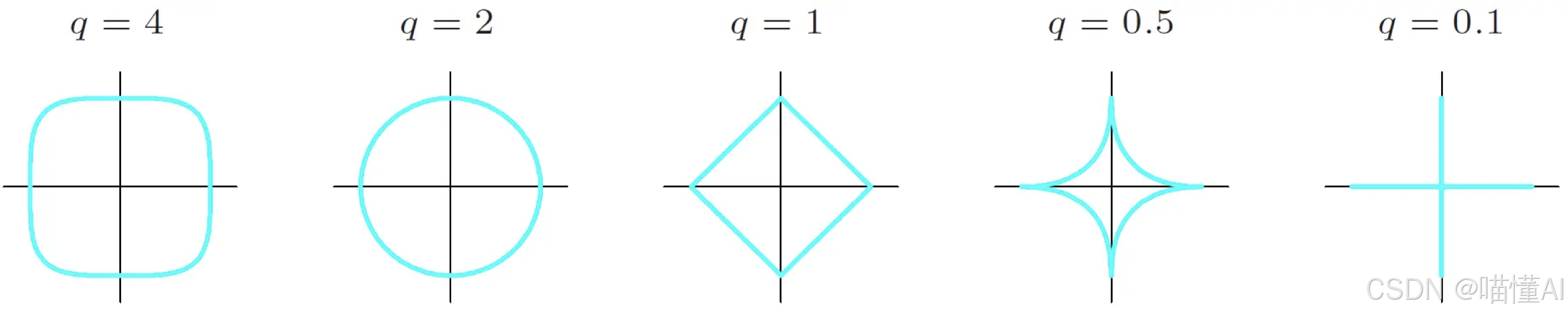
为什么L1正则可以进行特征筛选（稀疏解）

稀疏性是指许多参数值为0，这有助于特征选择和减少模型复杂度。

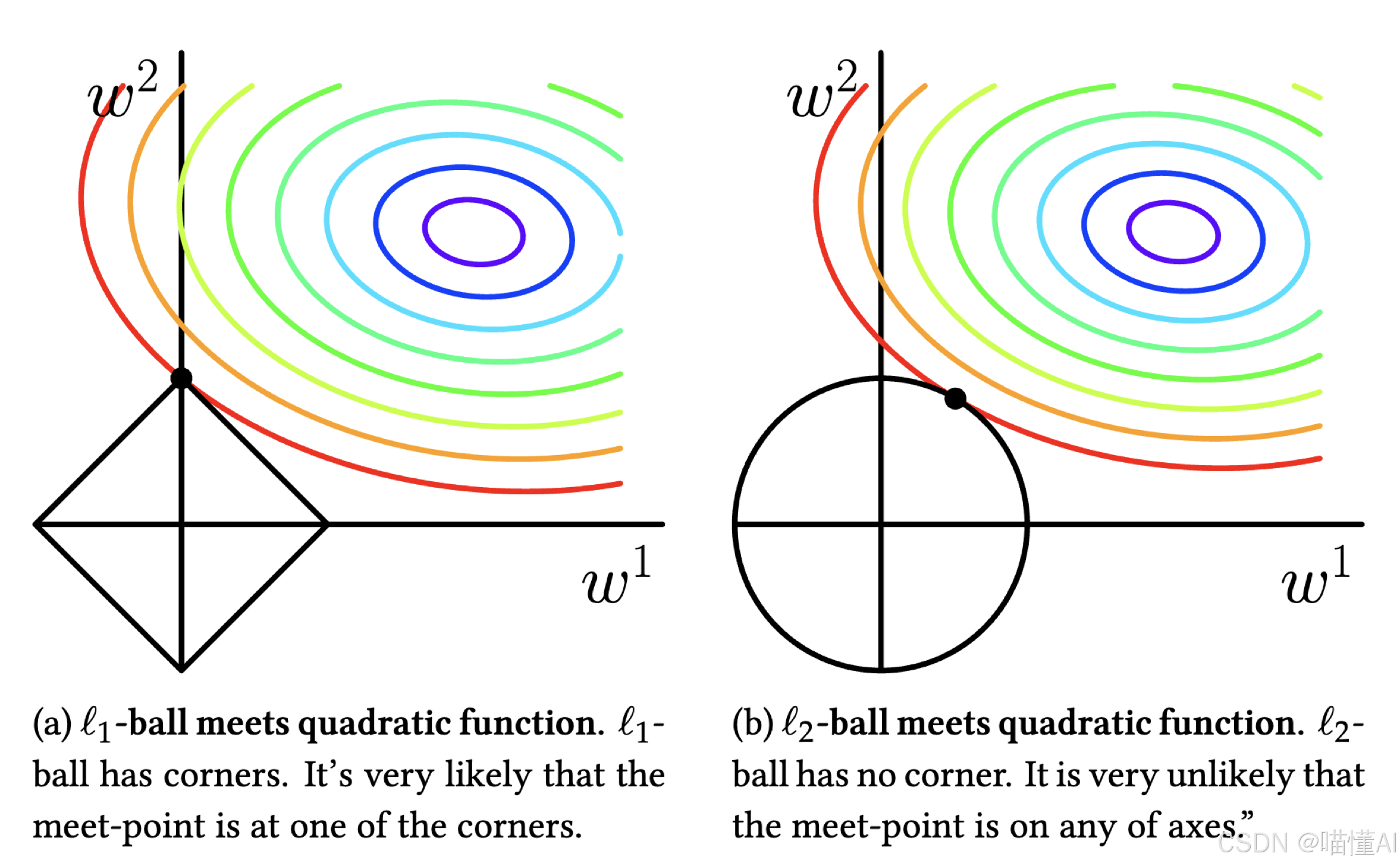
我们结合上面的L1和L2的可视化，尝试从几何角度来解释。

损失等高线（Loss Contours）：损失函数的等高线，代表不同损失值的集合，在一个椭圆移动时损失函数的值不变（类比等势线）

约束区域（Constraint Region）：L1或L2正则引入的约束。

• 对L1 Norm而言2维空间的约束区域是一个菱形（左图）
• 对L2 Norm而言2维空间的约束区域是一个圆形（右图）

L1和L2正则化的目标是找到损失函数的等值线和约束区域相交或相切的点，也就是加了正则化之后的损失函数的最优解。那么为什么L1正则会产生稀疏性呢？我们接着看。

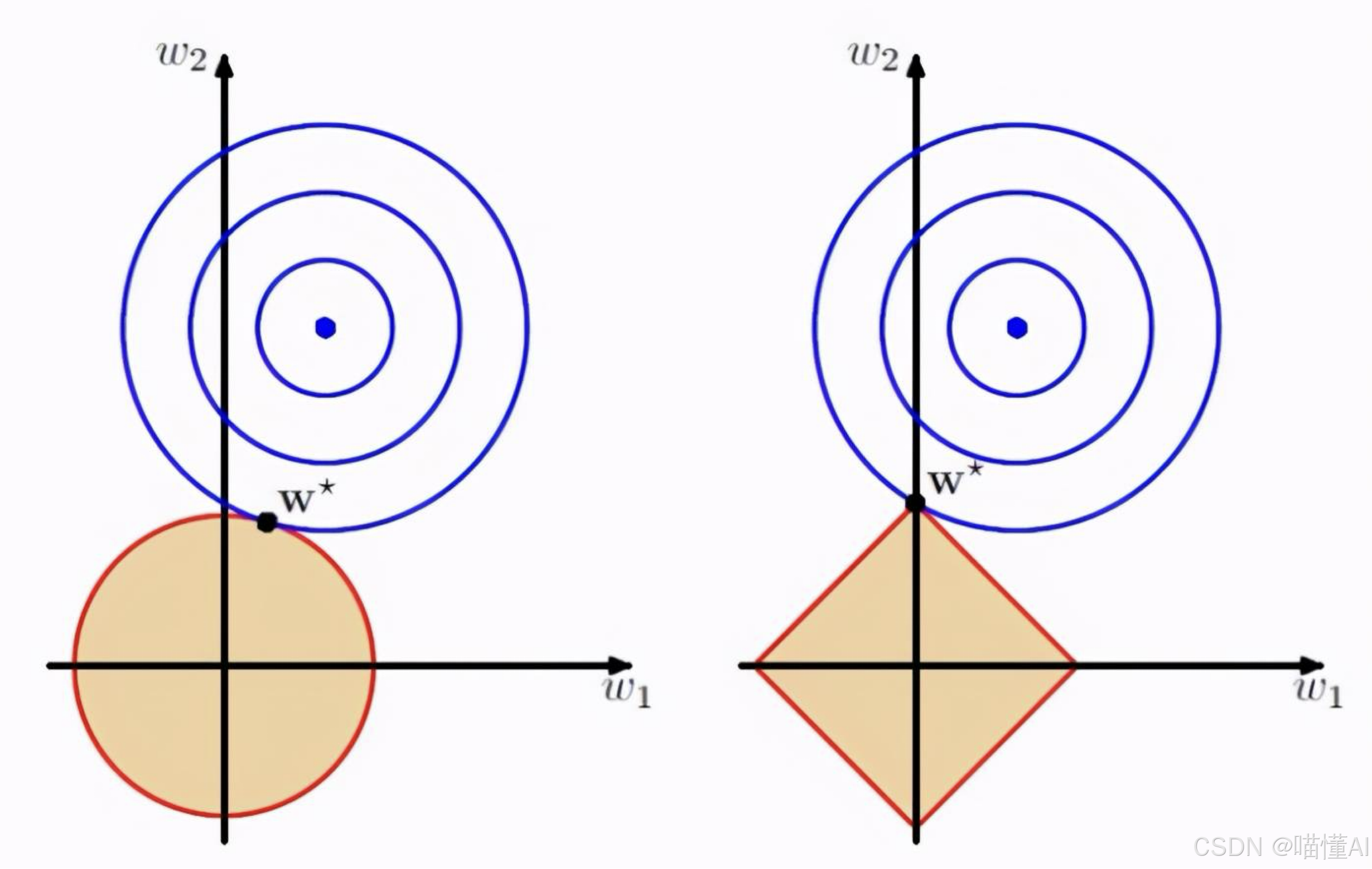
L1正则的菱形约束区域和损失函数等值线相交时，菱形的顶点是符合要求的概率较大的点，而顶点又在轴上，意味着（2维空间下）有一个参数会是零。

在高纬度空间可以以此类推，我们有很多参数时，L1的约束区域很可能在某些纬度的轴上和损失函数等值线相交，导致这些维度的参数为零，从而产生稀疏性。

反观L2正则，由于约束区域是圆形，交点出现在轴上的概率很小，因此尽管参数会得到约束惩罚，但不会归零，因此不会产生L1那样的稀疏解。