数据库工程师基础学习3---线性结构,数组,树与二叉树

1,线性结构

这里的线性表也包含链表,但是链表不一定是顺序存储的,在顺序存储中,逻辑上相邻的元素,物理上也相临.

这里可以看到,链表只是一种存储方式.
链表的缺点就是:只能顺序查找元素,查找元素的时间复杂度为o(n),但是插入和删除元素较快,而且不需要连续的存储空间

.以上是链表的改进.双链表的前驱节点指向前一个元素,后继节点,指向下一个元素.

这里注意,栈和队列也是一种线性表.并且如果top指针等于head指针,那么说明栈已满,如果top指针指向bottom指针,说明栈是空的.

链栈不需要设置头节点,只要设置一个指针top,用来添加删除元素就可以.

可以看到头节点,设置的意义在于让开始节点的操作与其他节点相同.

队列,第一种是顺序队列.可以说是每入队一个元素,rear指针后移一个,每出队一个,front指针后移一个,这里有个问题就是,e6无法入队,即使e1和e2已经出队.

为了解决以上问题,就提出了循环队列.

教材(78-80)了解

这里注意字符串是可以比较的,先比较的是首字母的ascii码

这里注意,字符串的链式存储可以一个节点存储多个字符.一个字符占用一个或多个字节.

一般来说,数组的长度是固定的(仅限于部分语言)

上图介绍了以行为主序和以列为主序,其实就是按行存,还是按列存.

这里是按行存储的地址计算公式推导过程.核心是看aij前面有多少个存储单元.同理,也就可以推导出按列存储的地址计算公式.


对于对称矩阵来说,可以将n方的数据压缩到n(n+1)/2,用等差数列求和公式得到.
这里的公式是在算,aij是数组中的第几个元素.
注意如果k从0开始编号,那么就是这个公式,如果从1开始编号,上面公式还需要加上1.
可以看到,公式分两部分.上面的部分是aij属于下三角部分,下面的公式,是aij属于上三角的部分.(这个时候只需要将i,j互换就可以.)

另外注意,这里是按行存储的情况.


以上是aij与k公式的推导过程.
首先i-1行的元素个数(第一行为2,所以为3(i-1)-1),加上这一行的第几个元素,这里利用i.j的关系.

用三元组来表示稀疏矩阵.

2,树与二叉树

教材90页

注意空树与子树的概念,还有有且仅有一个根节点.

双亲节点就是父节点.
节点的度,其实就是子节点的个数.如A的度为3,B的度为2.
注意,一棵树除去叶子节点,其他的节点叫做分支节点.从分支节点中再去掉根节点,叫做内部节点.
有序树简单来说,就是该树中不能交换顺序.

树和二叉树的定义都应用到递归的思想,并且二叉树最大的不同就是,节点数只能在0,1,2中取.并且区分左右.

第一条性质的推导如上.这里为什么i-1,因为第一层相当于2的0次方.最大节点数是从0次方开始变化的.

这里第二条性质,就是一个简单的等比数列求和.

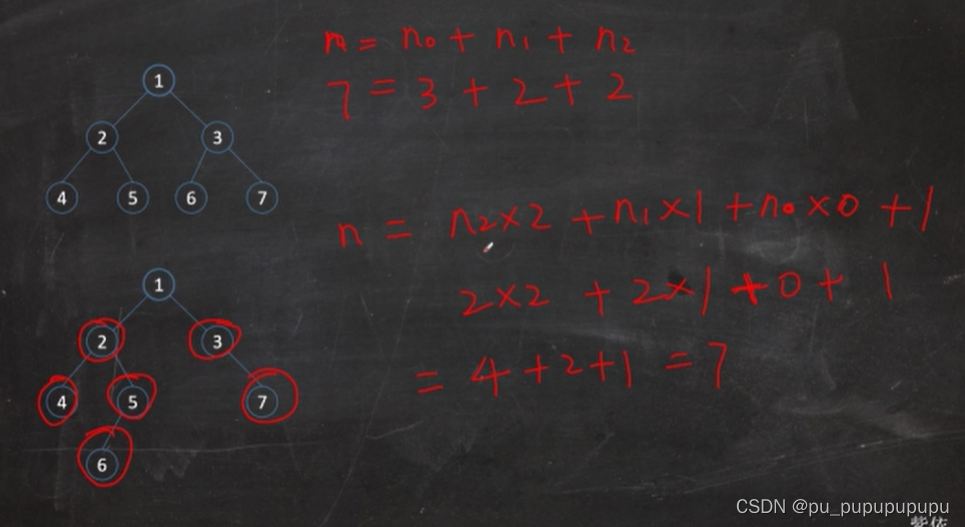
n表示总节点数,n0表示度为0的节点数,n1表示度为1的节点数,n2表示度为2的节点数.
所以我们从两个角度得到上面的两个式子.
第一个式子就是简单的求和.而第二个式子,是在算,每个节点的子节点个数.(度为2,有两个子节点.并且最后需要加上一个根节点.)

由此证明性质3.

满二叉树很好理解,完全二叉树就是在满二叉树的基础上,要求编号一样,而不要求(最后一层)是满的.但是要保证编号一致.
对于k深度的完全二叉树,那么其k-1层一定满的.最后一层可能不满.

这里第三条性质,i的左节点为2i,右节点为2i+1,(如果存在的话),当2i>n时,说明不存在左子节点.同理,可以逆过程求出其父节点的编号.这里INT表示向下取整,因为是2i和2i+1.
第二条性质:如果是满二叉树很明显是满足的(注意节点数是2的k次方-1,所以最后一层向下取整,也不计算在内.),不满的情况下,[]和INT都表示向下取整,就等于满的层数+1.

可以看到采用顺序存储,每一个节点在存储空间中的位置是确定的.对于完全二叉树还算有效率,但是对于一般的二叉树,会造成存储空间的浪费.

三叉链表还额外保留了父节点的信息.

注意前序,中序,后序,都是在说根节点的位置.
写这种次序的时候,将按照一颗颗子树进行遍历.

也可以说是霍夫曼树,路径长度简单来说就是:到根节点的线段数.
注意,节点的数字就是节点的权重.

那么,树的带权路径长度,是所有叶子节点之和,而不是所有节点之和.

所以中间的就是最优二叉树,权值相同,但带权路径最小.

构造最优二叉树的方法.

这个构造过程就是,先选择最小的两个权值,放在最深处.(8,15),然后将(8+15=23)权值和,放在原列表中(划去8,15,添加23),选出最小两个(22,23),得到45,选出两个(25,30)就构造完成了.其中23,45,55是辅助权值.并不是叶子节点.
注意最优二叉树不唯一,因为有些叶子节点可以调换位置.
教材96页


可以看到二叉查找树中序排列得到的序列是递增的.
并且二叉查找树在数据查找时,很方便.因为只需要比较与根节点的大小.