
本文同步更新在我的微信公众号里,地址:https://mp.weixin.qq.com/s/IPyI2Ee6Kzyv3wFAUN7NOQ
本文同步更新在我的知乎专栏里,地址:https://zhuanlan.zhihu.com/p/43190710
目录
1. 基本循环神经网络
传统的神经网络模型是从输入层到隐含层再到输出层的全连接,且同层的节点之间是无连接,网络的传播也是顺序的,但这种普通的网络结构对于许多问题却显得无能为力。例如,在自然语言处理中,如果要预测下一个单词,就需要知道前面的部分单词,因为一个句子中的单词之间是相互联系的,即有语义。这就需要一种新的神经网络,即循环神经网络RNN,循环神经网络对于序列化的数据有很强的模型拟合能力。具体的结构为:循环神经网络在隐含层会对之前的信息进行存储记忆,然后输入到当前计算的隐含层单元中,也就是隐含层的内部节点不再是相互独立的,而是互相有消息传递。隐含层的输入不仅可以由两部分组成,输入层的输出和隐含层上一时刻的输出,即隐含层内的节点自连;隐含层的输入还可以由三部分组成,输入层的输出、隐含层上一时刻的输出、上一隐含层的状态,即隐含层内的节点不仅自连还互连。结构如图1所示。
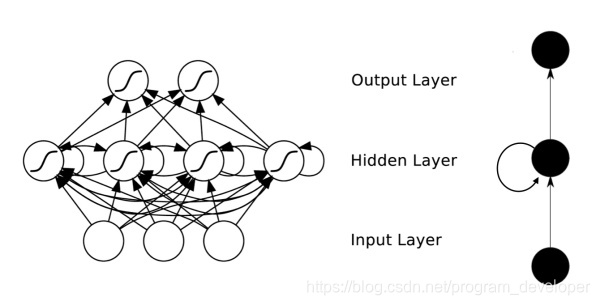
在图1中,可以看到隐含层节点间有消息的相互传递。为了更简单的理解,现在我们将RNN在时间坐标轴上展开成一个全神经网络,如图2所示。例如,对一个包含3个单词的语句,那么展开的网络便是一个有3层的神经网络,每一层代表一个单词。
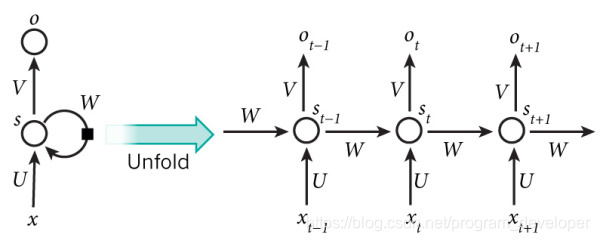
对于图2的网络,计算过程如下:
-
表示第
步(step)的输入。比如
为第二个词的词向量(
为第一个词);
-
为隐藏层的第t步的状态,它是网络的记忆单元。
根据当前输入层的输出与上一时刻隐藏层的状态
进行计算,如公式1所示。其中,U是输入层的连接矩阵,W是上一时刻隐含层到下一时刻隐含层的权重矩阵,f(x)一般是非线性的激活函数,如tanh或ReLU。
(1)
是第t步的输出。输出层是全连接层,即它的每个节点和隐含层的每个节点都互相连接,V是输出层的连接矩阵,g(x)是激活函数。
(2)
如果将(1)式循环带入(2)式可得:
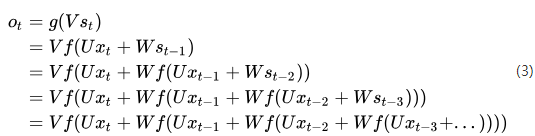
由式(3)可以看出,循环神经网络的输出值与前面多个时刻的历史输入值有关,这就是为何循环神经网络能够往前看任意多个输入值的原因,也就是为何循环神经网络能够对序列数据建模的原因。
在图2中,我们展示了一个单向循环神经网络,但是单向循环神经网络也有不足之处。从单向的结构中可以知道它的下一时刻预测输出是根据前面多个时刻的输入共同影响的,而有些时候预测可能需要由前面若干输入和后面若干输出共同决定,这样才会更加准确。
2. 双向循环神经网络
2.1 双向循环神经网络的介绍
对于语言模型来说,很多时候单向循环神经网络表现是不好的,比如下面这句话:
我的手机坏了,我打算____一部新手机。
可以想象,如果我们只看横线前面的词,手机坏了,那么我是打算修一修?换一部新的?还是大哭一场?这些都是无法确定的。但如果我们也看到了横线后面的词是『一部新手机』,那么,横线上的词填『买』的概率就大得多了。
对于上面的语言模型,单向循环神经网络是无法对此进行建模的。因此,我们需要用双向循环神经网络,如图3所示。
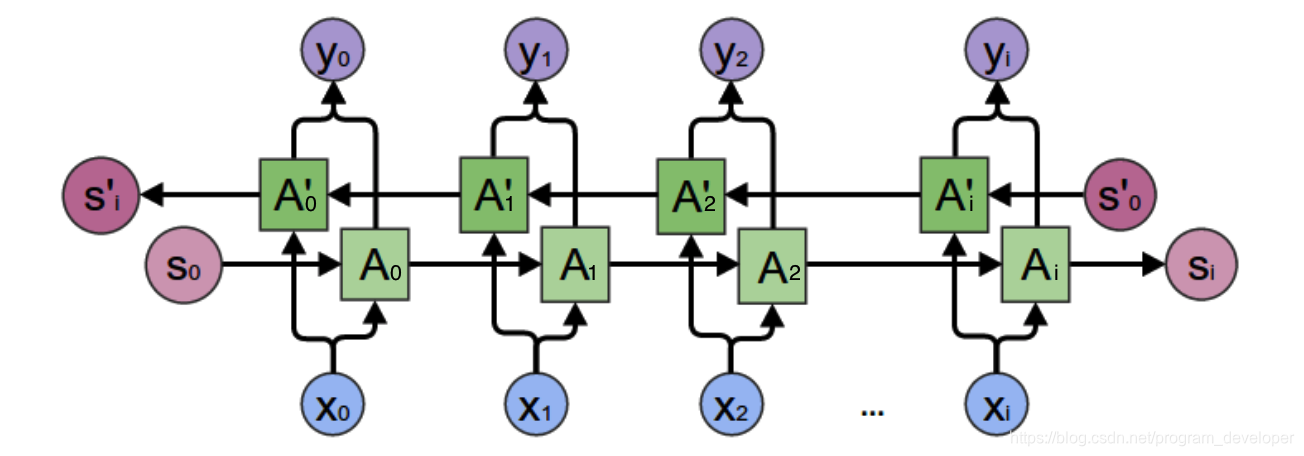
从图3中可以看出,双向循环神经网络的隐藏层要保存两个值,一个A参与正向计算,另一个值参与反向计算。我们以
的计算为例,推出循环神经网络的一般规律。最终的输出值
取决于
和
。其计算方式为公式4:
(4)
和
则分别计算为:
(5)
(6)
现在,我们已经可以看出一般的规律:正向计算时,隐藏层的值与
有关;反向计算时,隐藏层的值
与
有关;最终的输出取决于正向和反向计算的加和。现在,我们仿照式5和式6,写出双向循环神经网络的计算方法:
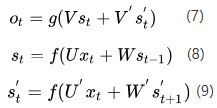
从上面三个公式我们可以看到,正向计算和反向计算不共享权重,也就是说U和U'、W和W'、V和V'都是不同的权重矩阵。
2.2 双向循环神经网络的训练
前向传播:
-
沿着时刻0到时刻i正向计算一遍,得到并保存每个时刻向前隐含层的输出。
-
沿着时刻i到时刻0反向计算一遍,得到并保存每个时刻向后隐含层的输出。
-
正向和反向都计算完所有输入时刻后,每个时刻根据向前向后隐含层得





 本文详细介绍了循环神经网络(RNN)的基础结构,包括基本的RNN、双向RNN和深度RNN。重点讨论了RNN的时间步长、参数共享以及训练算法BPTT。此外,还探讨了RNN面临的梯度消失和梯度爆炸问题,以及解决长距离依赖的挑战。最后,文中列举了RNN的各种架构,如1 to N、N to 1、N to N和N to M,展示了RNN在序列数据处理中的广泛应用。
本文详细介绍了循环神经网络(RNN)的基础结构,包括基本的RNN、双向RNN和深度RNN。重点讨论了RNN的时间步长、参数共享以及训练算法BPTT。此外,还探讨了RNN面临的梯度消失和梯度爆炸问题,以及解决长距离依赖的挑战。最后,文中列举了RNN的各种架构,如1 to N、N to 1、N to N和N to M,展示了RNN在序列数据处理中的广泛应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 684
684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








