【LeetCode】215. Kth Largest Element in an Array

我的个人微信公众号：Microstrong

微信公众号ID：MicrostrongAI

微信公众号介绍：Microstrong(小强)同学主要研究机器学习、深度学习、计算机视觉、智能对话系统相关内容，分享在学习过程中的读书笔记！期待您的关注，欢迎一起学习交流进步！

知乎主页：https://www.zhihu.com/people/MicrostrongAI/activities

Github：https://github.com/Microstrong0305

个人博客：https://blog.youkuaiyun.com/program_developer

215. Kth Largest Element in an Array

Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Example 1:

Input: [3,2,1,5,6,4] and k = 2
Output: 5

Example 2:

Input: [3,2,3,1,2,4,5,5,6] and k = 4
Output: 4

Note:
You may assume k is always valid, 1 ≤ k ≤ array's length.

解题思路：

（1）堆排序

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        """
        :param nums: List[int] 待排序列表
        :param k: int 第k大数值
        :return: int 返回值
        """
        length = len(nums)
        # 构建大顶堆
        for i in range(length // 2 - 1, -1, -1):
            self.adjustHeap(nums, i, length)

        count = 0
        for j in range(length - 1, -1, -1):
            count += 1
            if count == k:
                return nums[0]
            self.swap(nums, 0, j)
            length -= 1
            self.adjustHeap(nums, 0, length)

    def adjustHeap(self, nums, i, length):
        """
        :param nums: 待排序数组
        :param i: 指定以i为根结点排序
        :param length: 待排序数组长度
        :return:
        """
        while True:
            leftChild = i * 2 + 1
            if leftChild >= length:
                return
            if leftChild + 1 < length and nums[leftChild + 1] > nums[leftChild]:
                leftChild += 1
            if nums[leftChild] > nums[i]:
                self.swap(nums, i, leftChild)
                i = leftChild
            else:
                return

    def swap(self, nums, i, j):
        temp = nums[i]
        nums[i] = nums[j]
        nums[j] = temp
   

（2）大顶堆-Python的heapq库

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        from heapq import heappush, heapreplace
        # 使用大顶堆
        heap = []
        for i in range(len(nums)):
            if i < k:
                heappush(heap, nums[i])  # 将 nums[i] 压入堆中
            else:
                if nums[i] > heap[0]:
                    m = heapreplace(heap, nums[i])  # 弹出最小的元素，并将nums[i]压入堆中，返回弹出的元素
        return heap[0]

（3）基于Partition函数的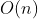算法

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:

        low, high = 0, len(nums) - 1

        def select_k(nums, low, high, k):
            if low == high:
                return nums[low]
            partitionIndex = self.partition(nums, low, high)
            index = high - partitionIndex + 1  # 找到的是第几大的值
            if index == k:
                return nums[partitionIndex]
            elif index < k:
                # 此时向左查找
                return select_k(nums, low, partitionIndex - 1, k - index)
            else:
                return select_k(nums, partitionIndex + 1, high, k)

        return select_k(nums, low, high, k)

    def partition(self, nums, low, high):
        pivot = nums[low]
        while low < high:
            while low < high and pivot <= nums[high]:
                high -= 1
            nums[low] = nums[high]
            while low < high and pivot > nums[low]:
                low += 1
            nums[high] = nums[low]

        nums[high] = pivot

        return high