2024ICPC上海站Just-in-Time Render Analysis题解

最新推荐文章于 2025-03-10 00:14:04 发布

priudy

最新推荐文章于 2025-03-10 00:14:04 发布

阅读量778

点赞数 14

CC 4.0 BY-SA版权

文章标签：算法 c++ 数据结构

本文链接：https://blog.youkuaiyun.com/priudy/article/details/145997164

经过寒假数据结构专项训练，本蒟蒻也是做出了acm生涯第一道金牌题，特此写一篇题解纪念一下（也是本蒟蒻第一篇题解），如果有问题恳请各位批评指正。

前置芝士：树链剖分+线段树

题意分析

阅读题面后，可以将题意抽象为一棵树，节点为矩形，给出矩形左下角(x1,y1)和右上角(x2,y2)的坐标，父节点和子节点的关系为父节点对应的矩形完全包含子节点对应的矩形。

操作 '^' 为根节点到k节点这条链上所有节点的权值加一或减一（此处在下文具体分析）；

操作 '?' 为询问这颗树上深度为k且权值大于0的节点个数。

实现方法

题目可以分成两部分实现，第一部分将矩阵关系转化为树，第二部分是树上操作。

建树

根据题意我们知道矩阵只有完全包含和不相交两种情况，可以用线段树维护。

二维矩阵可以联想到扫描线，可以将x坐标和y坐标离散化+排序，x坐标从小到大扫描，再遍历边界线是x的所有矩阵。如果x是矩阵左边界，相当于进入，就在y1-y2区间存储矩形编号，在递归路径中，矩阵的父节点一直更新为本线段树节点存储的最新编号；如果x是矩形右边界，相当于退出，就将y1-y2区间最新存储的编号出队，此编号就是此矩阵对应的编号，因为矩阵不重合。

这里解释一下为什么在线段树递归路径中，将此次操作的矩阵的编号的父节点要一直更新为线段树节点中存储的最新编号；如下图，根据遍历顺序，1号矩阵先被存储，再存储2号矩阵，此时在线段树中，2号矩阵被存储的位置，一定在1号矩阵存储位置的子树里。

当到右边界时，将y1-y2区间最新存储的编号出队，比如下图3和5号矩阵，不然会出现5的父节点为3的情况。

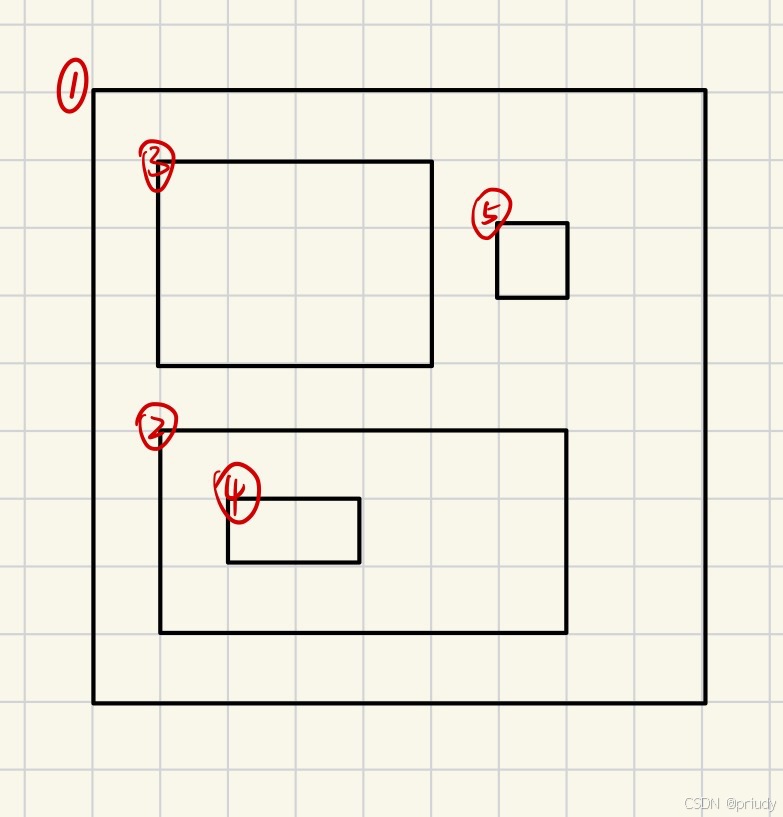
另外，由于我在后续的树上操作中用了树链剖分，所以我加入了一个边界矩形当作根节点。

struct juxing{
	int l,r;
	vector<int> a;
}ju[N*8];
void buildju(int p,int l,int r){
	ju[p]={l,r,{}};
	if(l==r)return;
	int m=(l+r)>>1ll;
	buildju(lc,l,m);
	buildju(rc,m+1,r);
}
void updateju(int p,int l,int r,int id){
	if(!ju[p].a.empty()){
		dep[id]=dep[ju[p].a.back()]+1;
		fa[id][0]=ju[p].a.back();
	}
	if(l<=ju[p].l&&ju[p].r<=r){
		ju[p].a.emplace_back(id);
		return;
	}
	if(ju[p].l==ju[p].r)return;
	int mid=(ju[p].l+ju[p].r)>>1;
	if(l<=mid)updateju(lc,l,r,id);
	if(r>mid)updateju(rc,l,r,id);	
}
void updatedel(int p,int l,int r){
	if(l<=ju[p].l&&ju[p].r<=r){
		ju[p].a.pop_back();
		return;
	}
	if(ju[p].l==ju[p].r)return;
	int mid=(ju[p].l+ju[p].r)>>1;
	if(l<=mid)updatedel(lc,l,r);
	if(r>mid)updatedel(rc,l,r);
}

	cin>>n>>m;
    a[1].x1=0;a[1].y1=0;a[1].x2=1e9+1;a[1].y2=1e9+1;
	n++;
	for(int i=2;i<=n;i++){
		cin>>a[i].x1>>a[i].y1>>a[i].x2>>a[i].y2;
	}
	for(int i=1;i<=n;i++){
		x[i]=a[i].x1,x[n+i]=a[i].x2;
	}
	sort(x+1,x+(n<<1)+1);
	int num=unique(x+1,x+(n<<1)+1)-x-1;
	for(int i=1;i<=n;i++){
		a[i].x1=lower_bound(x+1,x+num+1,a[i].x1)-x;
		a[i].x2=lower_bound(x+1,x+num+1,a[i].x2)-x;
	}
	for(int i=1;i<=n;i++){
		y[i]=a[i].y1,y[n+i]=a[i].y2;
	}
	sort(y+1,y+(n<<1)+1);
	num=unique(y+1,y+(n<<1)+1)-y-1;
	for(int i=1;i<=n;i++){
		a[i].y1=lower_bound(y+1,y+num+1,a[i].y1)-y;
		a[i].y2=lower_bound(y+1,y+num+1,a[i].y2)-y;
	}	
	for(int i=1;i<=(n);i++){
		x[i]=a[i].x1,x[n+i]=a[i].x2;
	}
	for(int i=1;i<=(n<<1);i++){
		p[i]=i;
	}
	sort(p+1,p+(n<<1)+1,cmp);
	buildju(1,1,num);
	for(int o=1;o<=(n<<1);o++){
		int i=p[o];
		if(i<=n){
			updateju(1,a[i].y1,a[i].y2,i);
			g[fa[i][0]].emplace_back(i);
			for(int j=1;j<=18;j++)
				fa[i][j]=fa[fa[i][j-1]][j-1];
		}
		else
			updatedel(1,a[i-n].y1,a[i-n].y2);
	}

树上操作

'^' 操作有点像染色，k节点染过了根节点到k节点整条链权值都减1，k节点没染过条链权值都加1。

这里对于链的操作用树链剖分+线段树更新，但是这里要注意，最后查询的是某深度权值大于0的节点数，但是如果根节点到k节点整条链权值都改变，不代表根节点的深度到k节点的深度的节点数都要改变。权值要加1时，只有节点权值等于0的节点的深度的节点数要加1，权值要减1时，只有节点权值等于1的节点的深度的节点数要加1。

所以我们要用两颗线段树维护，一颗线段树维护节点的权值和区间最大值和最小值，一颗线段树维护某深度权值大于0的节点数。

那我们怎么快速知道我们要更新的深度区间呢？因为每次权值更新是从k结点到根节点的更新，那么从子节点到根节点的权值一定是递增的，所以我们可以一直查找k结点的父结点，的父节点......找到所有权值符合条件的。但是显然太慢了，所以我们用倍增来查找。

如果操作权值减1：查找链上a结点的最小值，如果最小值是1，那么结点a的深度到结点k的深度区间就要减1。

如果操作权值加1：查找链上a结点的最大值，如果最大值是0，那么结点a的深度到结点k的深度区间就要加1。

其他的都是树链剖分和线段树基础操作。

int fa[N][20],dep[N],son[N],sz[N];
int top[N];
int id[N];
int cnt;
void dfs1(int now,int fat){
	fa[now][0]=fat,dep[now]=dep[fat]+1,sz[now]=1;
	for(int i=1;(1<<i)<=dep[now];i++){
		fa[now][i]=fa[fa[now][i-1]][i-1];
	}
	for(auto ne:g[now]){
		if(ne==fat)continue;
		dfs1(ne,now);
		sz[now]+=sz[ne];
		if(sz[son[now]]<sz[ne])son[now]=ne;
	}
}
void dfs2(int now,int t){
	top[now]=t;
	id[now]=++cnt;
	if(!son[now])return;
	dfs2(son[now],t);
	for(auto ne:g[now]){
		if(ne==fa[now][0]||ne==son[now])continue;
		dfs2(ne,ne);
	}
}
struct T{
	int l,r;
	int add,sum;
}tr[N*4];//存储深度对应结点数
void pushup(int p){
	tr[p].sum=tr[lc].sum+tr[rc].sum;
}
void pushdown(int p){
	if(tr[p].add){
		tr[lc].sum+=tr[p].add*(tr[lc].r-tr[lc].l+1);
		tr[rc].sum+=tr[p].add*(tr[rc].r-tr[rc].l+1);
		tr[lc].add+=tr[p].add;
		tr[rc].add+=tr[p].add;
		tr[p].add=0;
	}
}
void build(int p,int l,int r){
	tr[p]={l,r,0,0};
	if(l==r)return;
	int m=(l+r)>>1ll;
	build(lc,l,m);
	build(rc,m+1,r);
	pushup(p);
}
void update(int p,int l,int r,int k){
	if(l<=tr[p].l&&tr[p].r<=r){
		tr[p].add+=k;
		tr[p].sum+=k;
		return ;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1ll;
	if(l<=mid)update(lc,l,r,k);
	if(r>mid)update(rc,l,r,k);
	pushup(p);
}
int query(int p,int l,int r){
	if(l<=tr[p].l&&tr[p].r<=r){
		return tr[p].sum;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1ll;
	int res=0;
	if(l<=mid)res+=query(lc,l,r);
	if(r>mid)res+=query(rc,l,r);
	return res;
}

struct T1{
	int l,r;
	int maxl;int add;
	int minl;
}tr1[N*4];//存储节点权值 最大值和最小值
void pushup1(int p){
	tr1[p].maxl=max(tr1[lc].maxl,tr1[rc].maxl);
	tr1[p].minl=min(tr1[lc].minl,tr1[rc].minl);
}
void pushdown1(int p){
	if(tr1[p].add){
		tr1[rc].maxl+=tr1[p].add;
		tr1[lc].maxl+=tr1[p].add;
		tr1[lc].minl+=tr1[p].add;
		tr1[rc].minl+=tr1[p].add;		
		tr1[lc].add+=tr1[p].add;
		tr1[rc].add+=tr1[p].add;
		tr1[p].add=0;
	}
}
void build1(int p,int l,int r){
	tr1[p]={l,r,0,0,0};
	if(l==r)return;
	int m=(l+r)>>1ll;
	build1(lc,l,m);
	build1(rc,m+1,r);
	pushup1(p);
}
void update1(int p,int l,int r,int k){
	if(l<=tr1[p].l&&tr1[p].r<=r){
		tr1[p].minl+=k,
		tr1[p].maxl+=k,tr1[p].add+=k;		
		return ;
    }
	if(tr1[p].l==tr1[p].r)return;;
	pushdown1(p);
	int mid=(tr[p].l+tr[p].r)>>1ll;
	if(l<=mid)update1(lc,l,r,k);
	if(r>mid)update1(rc,l,r,k);
	pushup1(p);
}
void update_path(int u,int v,int k){
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		update1(1,id[top[u]],id[u],k);
		u=fa[top[u]][0]; 
	}
	if(dep[u]<dep[v])swap(u,v);
	update1(1,id[v],id[u],k);
}
int querymi(int p,int l,int r){
	if(l<=tr1[p].l&&tr1[p].r<=r){
		return tr1[p].minl;
	}
	pushdown1(p);
	int mid=(tr1[p].l+tr1[p].r)>>1ll;
	int res=0;
	if(l<=mid)res+=querymi(lc,l,r);
	if(r>mid)res+=querymi(rc,l,r);
	return res;
}
int query1(int p,int l,int r){
	if(l<=tr1[p].l&&tr1[p].r<=r){
		return tr1[p].maxl;
	}
	pushdown1(p);
	int mid=(tr1[p].l+tr1[p].r)>>1ll;
	int res=0;
	if(l<=mid)res+=query1(lc,l,r);
	if(r>mid)res+=query1(rc,l,r);
	return res;
}

    dfs1(root,-1);
	dfs2(root,root);
	build(1,1,n);
	build1(1,1,n);
	while(m--){
	  	char t;int k;
		cin>>t>>k;
		if(t=='^'){
			if(hx[k+1]){
				int tt=k+1;
				for(int i=18;i>=0;i--){
					if(fa[tt][i]>0&&querymi(1,id[fa[tt][i]],id[fa[tt][i]])==1){
						tt=fa[tt][i];
					}
				}
				if(querymi(1,id[tt],id[tt])==1) 
					update(1,dep[tt],dep[k+1],-1);
				update_path(1,k+1,-1);
				hx[k+1]=0;
			}
			else {
				int tt=k+1;
				for(int i=18;i>=0;i--){
					if(fa[tt][i]>0&&query1(1,id[fa[tt][i]],id[fa[tt][i]])==0){
						tt=fa[tt][i];
					}
				}
				if(query1(1,id[tt],id[tt])==0)	
					update(1,dep[tt],dep[k+1],1);
				update_path(1,k+1,1);
				hx[k+1]=1;
			}
		}
		else if(t=='?'){
			cout<<query(1,k+2,k+2)<<endl;
		}
	}

总结

这题是vpicpc上海站的时候感觉可以做的，但是当时时间不够了，加之比赛的时候没有想很明白，没能出的了，赛后补题的时候花了六七个小时，改了很多实现，有很多灵光乍现的地方，比如倍增找结点，用线段树建节点的关系。主要是没想明白就写，导致写了改改了写，希望之后做题的时候不要着急上机，先把整个思路捋清晰，确保可以实现了再写，避免脑子糊成依托。

还有就是跑的很慢，卡时间过的qaq。

完整代码

#include<bits/stdc++.h>
#define int long long
#define lc p<<1
#define rc p<<1|1
using namespace std;
int mod=998244353;
const int N=500025;
struct ju{
	int x1,y1,x2,y2;
}a[N];
int x[N<<1],y[N<<1],p[N<<1];
int n,m;
int hx[N];
vector<int> g[N];
int fa[N][20],dep[N],son[N],sz[N];
int top[N];
int id[N];
int cnt;
void dfs1(int now,int fat){
	fa[now][0]=fat,dep[now]=dep[fat]+1,sz[now]=1;
	for(int i=1;(1<<i)<=dep[now];i++){
		fa[now][i]=fa[fa[now][i-1]][i-1];
	}
	for(auto ne:g[now]){
		if(ne==fat)continue;
		dfs1(ne,now);
		sz[now]+=sz[ne];
		if(sz[son[now]]<sz[ne])son[now]=ne;
	}
}
void dfs2(int now,int t){
	top[now]=t;
	id[now]=++cnt;
	if(!son[now])return;
	dfs2(son[now],t);
	for(auto ne:g[now]){
		if(ne==fa[now][0]||ne==son[now])continue;
		dfs2(ne,ne);
	}
}
struct T{
	int l,r;
	int add,sum;
}tr[N*4];//存储深度对应结点数
void pushup(int p){
	tr[p].sum=tr[lc].sum+tr[rc].sum;
}
void pushdown(int p){
	if(tr[p].add){
		tr[lc].sum+=tr[p].add*(tr[lc].r-tr[lc].l+1);
		tr[rc].sum+=tr[p].add*(tr[rc].r-tr[rc].l+1);
		tr[lc].add+=tr[p].add;
		tr[rc].add+=tr[p].add;
		tr[p].add=0;
	}
}
void build(int p,int l,int r){
	tr[p]={l,r,0,0};
	if(l==r)return;
	int m=(l+r)>>1ll;
	build(lc,l,m);
	build(rc,m+1,r);
	pushup(p);
}
void update(int p,int l,int r,int k){
	if(l<=tr[p].l&&tr[p].r<=r){
		tr[p].add+=k;
		tr[p].sum+=k;
		return ;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1ll;
	if(l<=mid)update(lc,l,r,k);
	if(r>mid)update(rc,l,r,k);
	pushup(p);
}
int query(int p,int l,int r){
	if(l<=tr[p].l&&tr[p].r<=r){
		return tr[p].sum;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1ll;
	int res=0;
	if(l<=mid)res+=query(lc,l,r);
	if(r>mid)res+=query(rc,l,r);
	return res;
}

struct T1{
	int l,r;
	int maxl;int add;
	int minl;
}tr1[N*4];//存储节点权值 最大值和最小值
void pushup1(int p){
	tr1[p].maxl=max(tr1[lc].maxl,tr1[rc].maxl);
	tr1[p].minl=min(tr1[lc].minl,tr1[rc].minl);
}
void pushdown1(int p){
	if(tr1[p].add){
		tr1[rc].maxl+=tr1[p].add;
		tr1[lc].maxl+=tr1[p].add;
		tr1[lc].minl+=tr1[p].add;
		tr1[rc].minl+=tr1[p].add;		
		tr1[lc].add+=tr1[p].add;
		tr1[rc].add+=tr1[p].add;
		tr1[p].add=0;
	}
}
void build1(int p,int l,int r){
	tr1[p]={l,r,0,0,0};
	if(l==r)return;
	int m=(l+r)>>1ll;
	build1(lc,l,m);
	build1(rc,m+1,r);
	pushup1(p);
}
void update1(int p,int l,int r,int k){
	if(l<=tr1[p].l&&tr1[p].r<=r){
		tr1[p].minl+=k,
		tr1[p].maxl+=k,tr1[p].add+=k;		
		return ;
    }
	if(tr1[p].l==tr1[p].r)return;;
	pushdown1(p);
	int mid=(tr[p].l+tr[p].r)>>1ll;
	if(l<=mid)update1(lc,l,r,k);
	if(r>mid)update1(rc,l,r,k);
	pushup1(p);
}
void update_path(int u,int v,int k){
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		update1(1,id[top[u]],id[u],k);
		u=fa[top[u]][0]; 
	}
	if(dep[u]<dep[v])swap(u,v);
	update1(1,id[v],id[u],k);
}
int querymi(int p,int l,int r){
	if(l<=tr1[p].l&&tr1[p].r<=r){
		return tr1[p].minl;
	}
	pushdown1(p);
	int mid=(tr1[p].l+tr1[p].r)>>1ll;
	int res=0;
	if(l<=mid)res+=querymi(lc,l,r);
	if(r>mid)res+=querymi(rc,l,r);
	return res;
}
int query1(int p,int l,int r){
	if(l<=tr1[p].l&&tr1[p].r<=r){
		return tr1[p].maxl;
	}
	pushdown1(p);
	int mid=(tr1[p].l+tr1[p].r)>>1ll;
	int res=0;
	if(l<=mid)res+=query1(lc,l,r);
	if(r>mid)res+=query1(rc,l,r);
	return res;
}

//矩形的线段树
bool cmp(int x1,int x2){
	return x[x1]<x[x2];
}
struct juxing{
	int l,r;
	vector<int> a;
}ju[N*8];
void buildju(int p,int l,int r){
	ju[p]={l,r,{}};
	if(l==r)return;
	int m=(l+r)>>1ll;
	buildju(lc,l,m);
	buildju(rc,m+1,r);
}
void updateju(int p,int l,int r,int id){
	if(!ju[p].a.empty()&&dep[ju[p].a.back()]>=dep[id]){
		dep[id]=dep[ju[p].a.back()]+1;
		fa[id][0]=ju[p].a.back();
	}
	if(l<=ju[p].l&&ju[p].r<=r){
		ju[p].a.emplace_back(id);
		return;
	}
	if(ju[p].l==ju[p].r)return;
	int mid=(ju[p].l+ju[p].r)>>1;
	if(l<=mid)updateju(lc,l,r,id);
	if(r>mid)updateju(rc,l,r,id);	
}
void updatedel(int p,int l,int r){
	if(l<=ju[p].l&&ju[p].r<=r){
		ju[p].a.pop_back();
		return;
	}
	if(ju[p].l==ju[p].r)return;
	int mid=(ju[p].l+ju[p].r)>>1;
	if(l<=mid)updatedel(lc,l,r);
	if(r>mid)updatedel(rc,l,r);
}
void solve(){
	int root=1;
	cin>>n>>m;
    a[1].x1=0;a[1].y1=0;a[1].x2=1e9+1;a[1].y2=1e9+1;
	n++;
	for(int i=2;i<=n;i++){
		cin>>a[i].x1>>a[i].y1>>a[i].x2>>a[i].y2;
	}
	for(int i=1;i<=n;i++){
		x[i]=a[i].x1,x[n+i]=a[i].x2;
	}
	sort(x+1,x+(n<<1)+1);
	int num=unique(x+1,x+(n<<1)+1)-x-1;
	for(int i=1;i<=n;i++){
		a[i].x1=lower_bound(x+1,x+num+1,a[i].x1)-x;
		a[i].x2=lower_bound(x+1,x+num+1,a[i].x2)-x;
	}
	for(int i=1;i<=n;i++){
		y[i]=a[i].y1,y[n+i]=a[i].y2;
	}
	sort(y+1,y+(n<<1)+1);
	num=unique(y+1,y+(n<<1)+1)-y-1;
	for(int i=1;i<=n;i++){
		a[i].y1=lower_bound(y+1,y+num+1,a[i].y1)-y;
		a[i].y2=lower_bound(y+1,y+num+1,a[i].y2)-y;
	}	
	for(int i=1;i<=(n);i++){
		x[i]=a[i].x1,x[n+i]=a[i].x2;
	}
	for(int i=1;i<=(n<<1);i++){
		p[i]=i;
	}
	sort(p+1,p+(n<<1)+1,cmp);
	buildju(1,1,num);
	for(int o=1;o<=(n<<1);o++){
		int i=p[o];
		if(i<=n){
			updateju(1,a[i].y1,a[i].y2,i);
			g[fa[i][0]].emplace_back(i);
			for(int j=1;j<=18;j++)
				fa[i][j]=fa[fa[i][j-1]][j-1];
		}
		else
			updatedel(1,a[i-n].y1,a[i-n].y2);
	}
	
	dfs1(root,-1);
	dfs2(root,root);
	build(1,1,n);
	build1(1,1,n);
	while(m--){
	  	char t;int k;
		cin>>t>>k;
		if(t=='^'){
			if(hx[k+1]){
				int tt=k+1;
				for(int i=18;i>=0;i--){
					if(fa[tt][i]>0&&querymi(1,id[fa[tt][i]],id[fa[tt][i]])==1){
						tt=fa[tt][i];
					}
				}
				if(querymi(1,id[tt],id[tt])==1) 
					update(1,dep[tt],dep[k+1],-1);
				update_path(1,k+1,-1);
				hx[k+1]=0;
			}
			else {
				int tt=k+1;
				for(int i=18;i>=0;i--){
					if(fa[tt][i]>0&&query1(1,id[fa[tt][i]],id[fa[tt][i]])==0){
						tt=fa[tt][i];
					}
				}
				if(query1(1,id[tt],id[tt])==0)	
					update(1,dep[tt],dep[k+1],1);
				update_path(1,k+1,1);
				hx[k+1]=1;
			}
		}
		else if(t=='?'){
			cout<<query(1,k+2,k+2)<<endl;
		}
	}
	return;
}
signed main() {
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	int T_case=1;
	//cin>>T_case;
	while(T_case--){
		solve();
	}
    return 0;
}