深度学习之全连接神经网络（四）

原创于 2025-08-28 22:25:30 发布 · 1.2k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能 #深度学习 #神经网络 #python #pytorch

六、反向传播算法

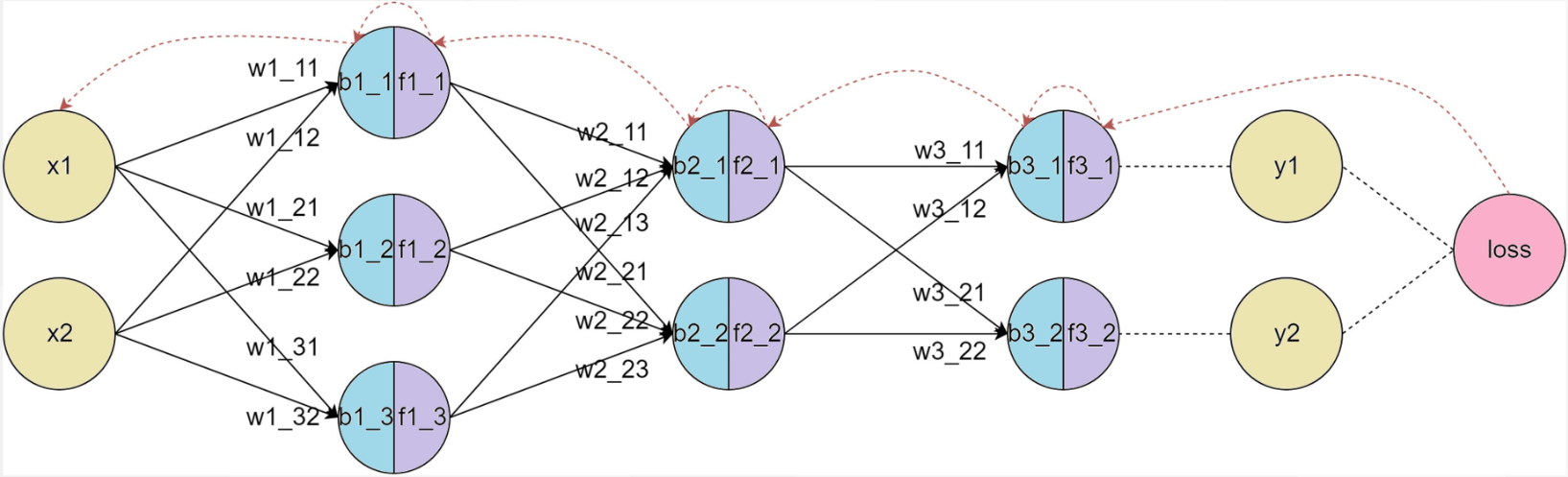
反向传播（Back Propagation，简称BP）算法是用于训练神经网络的核心算法之一，它通过计算损失函数（如均方误差或交叉熵）相对于每个权重参数的梯度，来优化神经网络的权重。

1. 前向传播

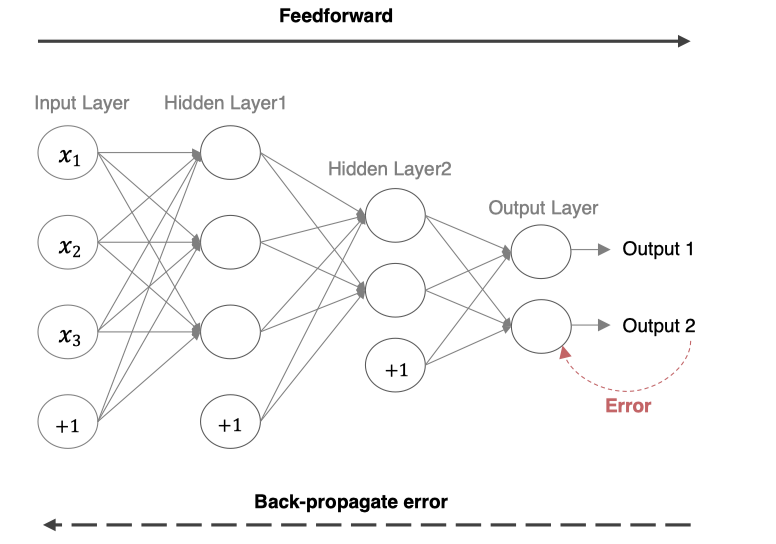
前向传播（Forward Propagation）把输入数据经过各层神经元的运算并逐层向前传输，一直到输出层为止。

1.1 数学表达

下面是一个简单的三层神经网络（输入层、隐藏层、输出层）前向传播的基本步骤分析。

1.1.1 输入层到隐藏层

给定输入 $x$ 和权重矩阵 $W_1$ 及偏置向量 $b_1$ ，隐藏层的输出（激活值）计算如下：

$z^{(1)} = W_1 \cdot x + b_1$

将 $z^{(1)}$ 通过激活函数 σ进行激活：

$a^{(1)} = \sigma(z^{(1)})$

1.1.2 隐藏层到输出层

隐藏层的输出 $a^{(1)}$ 通过输出层的权重矩阵 $W_2$ 和偏置 $b_2$ 生成最终的输出：

$z^{(2)} = W_2 \cdot a^{(1)} + b_2$

输出层的激活值 $a^{(2)}$ 是最终的预测结果：

$y_{\text{pred}} = a^{(2)} = \sigma(z^{(2)})$

1.2 作用

前向传播的主要作用是：

计算神经网络的输出结果，用于预测或计算损失。
在反向传播中使用，通过计算损失函数相对于每个参数的梯度来优化网络。

2. BP基础之梯度下降算法

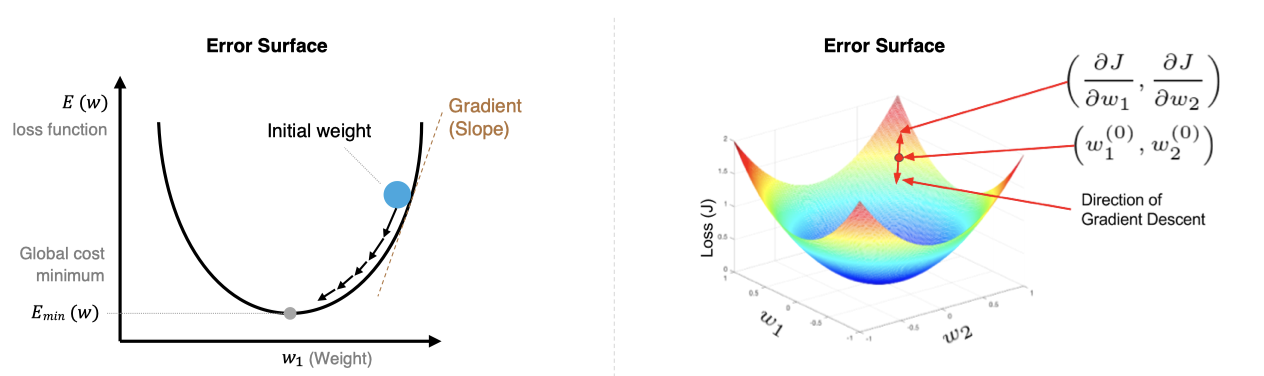
梯度下降算法的目标是找到使损失函数 $L(\theta)$ 最小的参数 $\theta$ ，其核心是沿着损失函数梯度的负方向更新参数，以逐步逼近局部或全局最优解，从而使模型更好地拟合训练数据。

2.1 数学描述

简单回顾下数学知识。

2.1.1 数学公式

$$
w_{ij}^{new}= w_{ij}^{old} - \alpha \frac{\partial E}{\partial w_{ij}}
$$

其中， $\alpha$ 是学习率：

学习率太小，每次训练之后的效果太小，增加时间和算力成本。
学习率太大，大概率会跳过最优解，进入无限的训练和震荡中。
解决的方法就是，学习率也需要随着训练的进行而变化。

学习率太大，大概率会跳过最优解，进入无限的训练和震荡中。
解决的方法就是，学习率也需要随着训练的进行而变化。

2.1.2 过程阐述

初始化参数：随机初始化模型的参数 $\theta$ ，如权重 W和偏置 b。
计算梯度：损失函数 $L(\theta)$ 对参数 $\theta$ 的梯度 $\nabla_\theta L(\theta)$ ，表示损失函数在参数空间的变化率。
更新参数：按照梯度下降公式更新参数： $\theta := \theta - \alpha \nabla_\theta L(\theta)$ ，其中， $\alpha$ 是学习率，用于控制更新步长。
迭代更新：重复【计算梯度和更新参数】步骤，直到某个终止条件（如梯度接近0、不再收敛、完成迭代次数等）。

2.2 传统下降方式

根据计算梯度时数据量不同，常见的方式有：

2. 2.1 批量梯度下降

Batch Gradient Descent BGD

特点：
- 每次更新参数时，使用整个训练集来计算梯度。
优点：
- 收敛稳定，能准确地沿着损失函数的真实梯度方向下降。
- 适用于小型数据集。
缺点：
- 对于大型数据集，计算量巨大，更新速度慢。
- 需要大量内存来存储整个数据集。
公式：

$$
\theta = \theta - \alpha \frac{1}{m} \sum_{i=1}^{m} \nabla_\theta L(\hat{y}^{(i)}, y^{(i)})
$$

其中，m 是训练集样本总数， $x^{(i)}, y^{(i)}$ 是第 i 个样本及其标签， $\hat{y}^{(i)}$ 是第 i 个样本预测值。

例如，在训练集中有100个样本，迭代50轮。

那么在每一轮迭代中，都会一起使用这100个样本，计算整个训练集的梯度，并对模型更新。

所以总共会更新50次梯度。

因为每次迭代都会使用整个训练集计算梯度，所以这种方法可以得到准确的梯度方向。

但如果数据集非常大，那么就导致每次迭代都很慢，计算成本就会很高。

示例：

     x = torch.randn(1000, 10)
     y = torch.randn(1000, 1)
 
     dataset = TensorDataset(x, y)
     dataloader = DataLoader(dataset, batch_size=len(dataset))
 
     model = nn.Linear(10, 1)
     criterion = nn.MSELoss()
     optimizer = optim.SGD(model.parameters(), lr=0.01)
 
     epochs = 100
 
     for epoch in range(epochs):
         for b_x, b_y in dataloader:
             optimizer.zero_grad()
             output = model(b_x)
             loss = criterion(output, b_y)
             loss.backward()
             optimizer.step()
 
             print('Epoch %d, Loss: %f' % (epoch, loss.item()))

2.2.2 随机梯度下降

Stochastic Gradient Descent, SGD

特点：
- 每次更新参数时，仅使用一个样本来计算梯度。
优点：
- 更新频率高，计算快，适合大规模数据集。
- 能够跳出局部最小值，有助于找到全局最优解。
缺点：
- 收敛不稳定，容易震荡，因为每个样本的梯度可能都不完全代表整体方向。
- 需要较小的学习率来缓解震荡。
公式：

$$
\theta = \theta - \alpha \nabla_\theta L(\hat{y}^{(i)}, y^{(i)})
$$

其中， $x^{(i)}, y^{(i)}$ 是当前随机抽取的样本及其标签。

例如，如果训练集有100个样本，迭代50轮，那么每一轮迭代，会遍历这100个样本，每次会计算某一个样本的梯度，然后更新模型参数。

换句话说，100个样本，迭代50轮，那么就会更新100*50=5000次梯度。

因为每次只用一个样本训练，所以迭代速度会非常快。

但更新的方向会不稳定，这也导致随机梯度下降，可能永远都不会收敛。

不过也因为这种震荡属性，使得随机梯度下降，可以跳出局部最优解。

这在某些情况下，是非常有用的。

示例：

     x = torch.randn(1000, 10)
     y = torch.randn(1000, 1)
 
     dataset = TensorDataset(x, y)
     dataloader = DataLoader(dataset, batch_size=1)
 
     model = nn.Linear(10, 1)
     criterion = nn.MSELoss()
     optimizer = optim.SGD(model.parameters(), lr=0.01)
 
     epochs = 100
 
     for epoch in range(epochs):
         for b_x, b_y in dataloader:
             optimizer.zero_grad()
             output = model(b_x)
             loss = criterion(output, b_y)
             loss.backward()
             optimizer.step()
 
             print('Epoch %d, Loss: %f' % (epoch, loss.item()))

2.2.3 小批量梯度下降

Mini-batch Gradient Descent MGBD

特点：
- 每次更新参数时，使用一小部分训练集（小批量）来计算梯度。
优点：
- 在计算效率和收敛稳定性之间取得平衡。
- 能够利用向量化加速计算，适合现代硬件（如GPU）。
缺点：
- 选择适当的批量大小比较困难；批量太小则接近SGD，批量太大则接近批量梯度下降。
- 通常会根据硬件算力设置为32\64\128\256等2的次方。
公式：

$$
\theta := \theta - \alpha \frac{1}{b} \sum_{i=1}^{b} \nabla_\theta L(\hat{y}^{(i)}, y^{(i)})
$$

其中，b 是小批量的样本数量，也就是 $batch\_size$ 。

例如，如果训练集中有100个样本，迭代50轮。

如果设置小批量的数量是20，那么在每一轮迭代中，会有5次小批量迭代。

换句话说，就是将100个样本分成5个小批量，每个小批量20个数据，每次迭代用一个小批量。

因此，按照这样的方式，会对梯度，进行50轮*5个小批量=250次更新。

示例：

     x = torch.randn(1000, 10)
     y = torch.randn(1000, 1)
 
     dataset = TensorDataset(x, y)
     # 小批量梯度下降，每批次100个样本
     dataloader = DataLoader(dataset, batch_size=100, shuffle=True)
 
     model = nn.Linear(10, 1)
     criterion = nn.MSELoss()
     optimizer = optim.SGD(model.parameters(), lr=0.01)
 
     epochs = 100
 
     for epoch in range(epochs):
         for b_x, b_y in dataloader:
             optimizer.zero_grad()
             output = model(b_x)
             loss = criterion(output, b_y)
             loss.backward()
             optimizer.step()
 
             print('Epoch %d, Loss: %f' % (epoch, loss.item()))

2.3 存在的问题

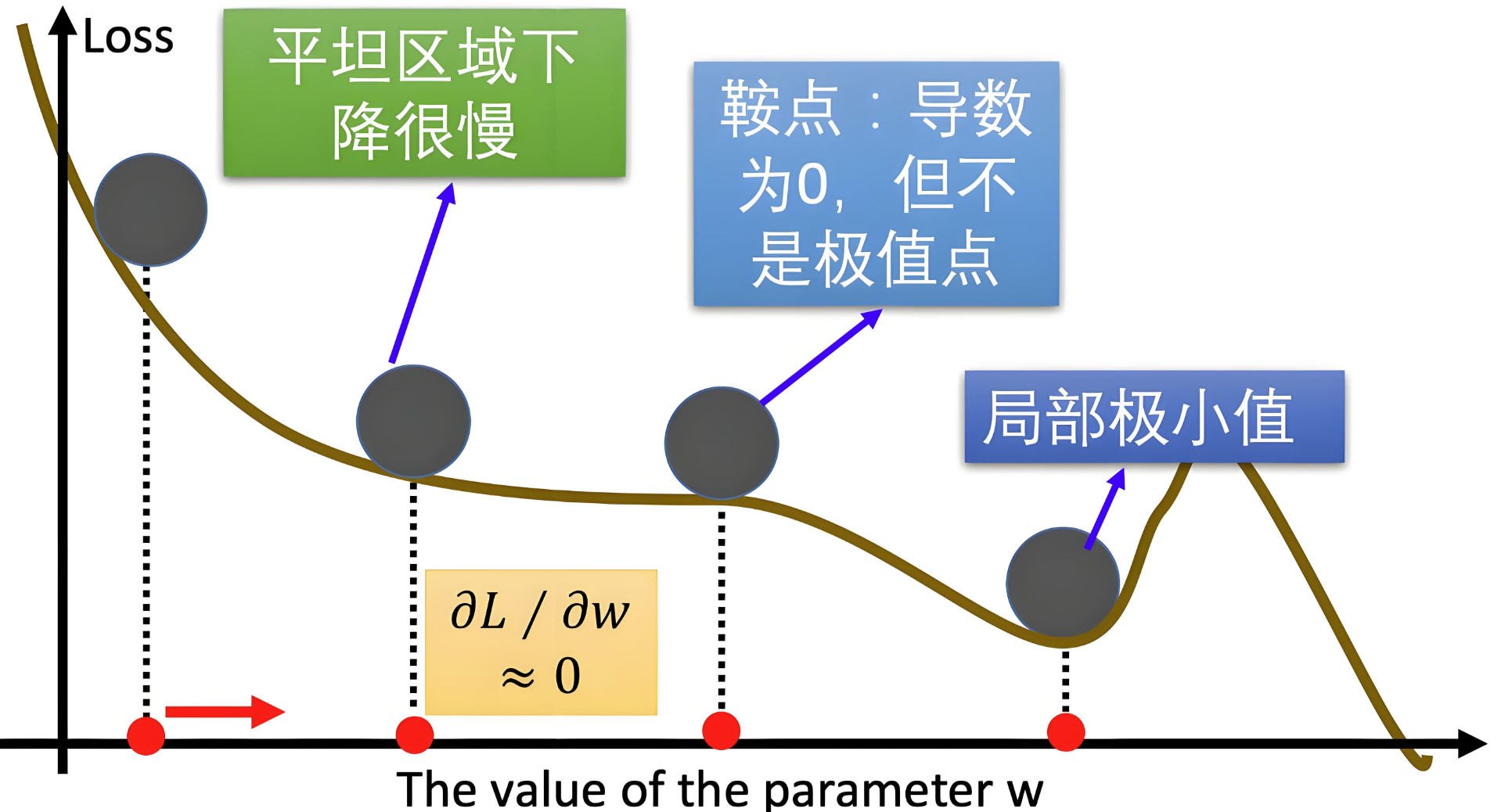
收敛速度慢：BGD和MBGD使用固定学习率，太大会导致震荡，太小又收敛缓慢。
局部最小值和鞍点问题：SGD在遇到局部最小值或鞍点时容易停滞，导致模型难以达到全局最优。
训练不稳定：SGD中的噪声容易导致训练过程中不稳定，使得训练陷入震荡或不收敛。

2.4 优化下降方式

通过对标准的梯度下降进行改进，来提高收敛速度或稳定性。

2.4.1 指数加权平均

我们平时说的平均指的是将所有数加起来除以数的个数，很单纯的数学。再一个是移动平均数，指的是计算最近邻的N个数来获得平均数，感觉比纯粹的直接全部求均值高级一点。

指数加权平均：Exponential Moving Average，简称EMA，是一种平滑时间序列数据的技术，它通过对过去的值赋予不同的权重来计算平均值。与简单移动平均不同，EMA赋予最近的数据更高的权重，较远的数据则权重较低，这样可以更敏感地反映最新的变化趋势。

比如今天股市的走势，和昨天发生的国际事件关系很大，和6个月前发生的事件关系相对肯定小一些。

给定时间序列 $\{x_t\}$ ，EMA在每个时刻 t 的值可以通过以下递推公式计算：

当t=1时：

$$
v_0 = x_0
$$

当t>1时：

$$
v_t = \beta v_{t-1} + (1 - \beta) x_t
$$

其中：

$v_t$ 是第 t 时刻的EMA值；
$x_t$ 是第 t 时刻的观测值；
$\beta$ 是平滑系数，取值范围为 $0\leq \beta < 1$ 。 $\beta$ 越接近 1，表示对历史数据依赖性越高；越接近 0 则越依赖当前数据。

公式推导：

$$
v_t = \beta v_{t-1} + (1 - \beta) x_t\\ v_{t-1} = \beta v_{t-2} + (1 - \beta) x_{t-1}\\ ...\\ 那么：\\ v_t = \beta v_{t-1} + (1 - \beta) x_t=\beta^2 v_{t-2} + \beta(1 - \beta) x_{t-1} + (1 - \beta) x_t\\ =\beta^3 v_{t-3} + \beta^2(1 - \beta) x_{t-2} + \beta(1 - \beta) x_{t-1} + (1 - \beta) x_t\\ ...\\ =\beta^t {x_0} + \beta^{t-1}(1 - \beta) x_{1} + \beta^{t-2}(1 - \beta) x_{2} + ... + (1 - \beta) x_t\\ =\beta^t {x_0} + (1 - \beta)\Sigma_{i=1}^n\beta^{t-i}x_i
$$

从上述公式可知：

当 β接近 1 时， $\beta ^k$ 衰减较慢，因此历史数据的权重较高。
当 β接近 0 时， $\beta ^k$ 衰减较快，因此历史数据的权重较低。

示例

假设我们有一组数据 x=[1,2,3,4,5]，我们选择 β=0.1和β=0.9 来计算 EMA。

（1）β=0.1

初始化：

$EMA_0=x_0=1$
计算后续值：

$$
EMA_1=0.1×1+0.9×2=1.9\\ EMA_2=0.1×1.9+0.9×3=2.89\\ EMA_3=0.1×2.89+0.9×4=3.889\\ EMA_4=0.1×3.889+0.9×5=4.8889
$$

最终，EMA 的值为 [1,1.9,2.89,3.889,4.8889]。

（2）β=0.9

初始化：

$$EMA_0=x_0=1$$
计算后续值：

$$
EMA_1=0.9×1+0.1×2=1.1\\ EMA_2=0.9×1.1+0.1×3=1.29\\ EMA_3=0.9×1.29+0.1×4=1.561\\ EMA_4=0.9×1.561+0.1×5=1.9049
$$

最终，EMA 的值为 [1,1.1,1.29,1.561,1.9049]。

可以看到：

当 β=0.9 时，历史数据的权重较高，平滑效果较强。EMA值变化缓慢（新数据仅占10%权重），滞后明显。
当 β=0.1时，近期数据的权重较高，平滑效果较弱。EMA值快速逼近最新数据（每次新数据占90%权重）。

2.4.2 Momentum

动量（Momentum）是对梯度下降的优化方法，可以更好地应对梯度变化和梯度消失问题，从而提高训练模型的效率和稳定性。它通过引入 指数加权平均 来积累历史梯度信息，从而在更新参数时形成“动量”，帮助优化算法更快地越过局部最优或鞍点。

梯度更新算法包括两个步骤：

a. 更新动量项

首先计算当前的动量项 $v_t$ ： $v_{t} = \beta v_{t-1} + (1 - \beta) \nabla_\theta J(\theta_t)$ 其中：

$v_{t-1}$ 是之前的动量项；
$\beta$ 是动量系数（通常为 0.9）；
$\nabla_\theta J(\theta_t)$ 是当前的梯度；

b. 更新参数

利用动量项更新参数：

$$
v_{t}=\beta v_{t-1}+(1-\beta)\nabla_\theta J(\theta_t) \\ \theta_{t}=\theta_{t-1}-\eta v_{t}
$$

特点：

惯性效应： 该方法加入前面梯度的累积，这种惯性使得算法沿着当前的方向继续更新。如遇到鞍点，也不会因梯度逼近零而停滞。
减少震荡： 该方法平滑了梯度更新，减少在鞍点附近的震荡，帮助优化过程稳定向前推进。
加速收敛： 该方法在优化过程中持续沿着某个方向前进，能够更快地穿越鞍点区域，避免在鞍点附近长时间停留。

在方向上的作用：

（1）梯度方向一致时

如果梯度在多个连续时刻方向一致（例如，一直指向某个方向），Momentum 会逐渐积累动量，使更新速度加快。
例如，假设梯度在多个时刻都是正向的，动量 $v_t$ 会逐渐增大，从而加速参数更新。

（2）梯度方向不一致时

如果梯度方向在不同时刻不一致（例如，来回震荡），Momentum 会通过积累的历史梯度信息部分抵消这些震荡。
例如，假设梯度在一个时刻是正向的，下一个时刻是负向的，动量 $v_t$ 会平滑这些变化，使更新路径更加稳定。

（3）局部最优或鞍点附近

在局部最优或鞍点附近，梯度可能会变得很小，导致标准梯度下降法停滞。
Momentum 通过积累历史梯度信息，可以帮助参数更新越过这些平坦区域。

动量方向与梯度方向一致

（1）梯度方向一致时

如果梯度在多个连续时刻方向一致（例如，一直指向某个方向），动量会逐渐积累，动量方向与梯度方向一致。
例如，假设梯度在多个时刻都是正向的，动量 $v_t$ 会逐渐增大，从而加速参数更新。

（2）几何意义

在优化问题中，如果损失函数的几何形状是 平滑且单调 的（例如，一个狭长的山谷），梯度方向会保持一致。
在这种情况下，动量方向与梯度方向一致，Momentum 会加速参数更新，帮助算法更快地收敛。

动量方向与梯度方向不一致

（1）梯度方向不一致时

如果梯度方向在不同时刻不一致（例如，来回震荡），动量方向可能会与当前梯度方向不一致。
例如，假设梯度在一个时刻是正向的，下一个时刻是负向的，动量 $v_t$ 会平滑这些变化，使更新路径更加稳定。

（2）几何意义

在优化问题中，如果损失函数的几何形状是 复杂且非凸 的（例如，存在多个局部最优或鞍点），梯度方向可能会在不同时刻发生剧烈变化。
在这种情况下，动量方向与梯度方向可能不一致，Momentum 会通过积累的历史梯度信息部分抵消这些震荡，使更新路径更加平滑。

总结：

动量项更新：利用当前梯度和历史动量来计算新的动量项。
权重参数更新：利用更新后的动量项来调整权重参数。
梯度计算：在每个时间步计算当前的梯度，用于更新动量项和权重参数。

Momentum 算法是对梯度值的平滑调整，但是并没有对梯度下降中的学习率进行优化。

示例：

 # 定义模型和损失函数
 model = nn.Linear(10, 1)
 criterion = nn.MSELoss()
 optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)  # PyTorch 中 momentum 直接作为参数
 
 # 模拟数据
 X = torch.randn(100, 10)
 y = torch.randn(100, 1)
 
 # 训练循环
 for epoch in range(100):
     optimizer.zero_grad()
     outputs = model(X)
     loss = criterion(outputs, y)
     loss.backward()
     optimizer.step()
     print(f'Epoch {epoch}, Loss: {loss.item():.4f}')

2.4.3 AdaGrad

AdaGrad（Adaptive Gradient Algorithm）为每个参数引入独立的学习率，它根据历史梯度的平方和来调整这些学习率。具体来说，对于频繁更新的参数，其学习率会逐渐减小；而对于更新频率较低的参数，学习率会相对较大。AdaGrad避免了统一学习率的不足，更多用于处理稀疏数据和梯度变化较大的问题。

AdaGrad流程：

初始化：
- 初始化参数 $\theta_0$ 和学习率 $\eta$ 。
- 将梯度累积平方的向量 $G_0$ 初始化为零向量。
梯度计算：
- 在每个时间步 t，计算损失函数 $J(\theta)$ 对参数 $\theta$ 的梯度 $g_t = \nabla_\theta J(\theta_t)$ 。
累积梯度的平方：
- 对每个参数 i 累积梯度的平方：
  
  $$
  G_{t} = G_{t-1} + g_{t}^2\\
  $$
  
  其中 $G_{t}$ 是累积的梯度平方和， $g_{t}$ 是第 i 个参数在时间步t 的梯度。
  
  推导：
  
  $$
  G_{t} = G_{t-1} + g_{t}^2=G_{t-2} + g_{t-1}^2 + g_{t}^2 = ... = g_{1}^2 + ... + g_{t-1}^2 + g_{t}^2
  $$
参数更新：
- 利用累积的梯度平方来更新参数：
  
  $$
  \theta_{t} = \theta_{t-1} - \frac{\eta}{\sqrt{G_{t} + \epsilon}} g_{t}
  $$
- 其中：
  - $\eta$ 是全局的初始学习率。
  - $\epsilon$ 是一个非常小的常数，用于避免除零操作（通常取 $10^{-8}$ ）。
  - $\frac{\eta}{\sqrt{G_{t} + \epsilon}}$ 是自适应调整后的学习率。

AdaGrad 为每个参数分配不同的学习率：

对于梯度较大的参数， $Gt$ 较大，学习率较小，从而避免更新过快。
对于梯度较小的参数， $Gt$ 较小，学习率较大，从而加快更新速度。

可以将 AdaGrad 类比为：

梯度较大的参数：类似于陡峭的山坡，需要较小的步长（学习率）以避免跨度过大。
梯度较小的参数：类似于平缓的山坡，可以采取较大的步长（学习率）以加快收敛。

优点：

自适应学习率：由于每个参数的学习率是基于其梯度的累积平方和 $G_{t,i}$ 来动态调整的，这意味着学习率会随着时间步的增加而减少，对梯度较大且变化频繁的方向非常有用，防止了梯度过大导致的震荡。
适合稀疏数据：AdaGrad 在处理稀疏数据时表现很好，因为它能够自适应地为那些较少更新的参数保持较大的学习率。

缺点：

学习率过度衰减：随着时间的推移，累积的时间步梯度平方值越来越大，导致学习率逐渐接近零，模型会停止学习。
不适合非稀疏数据：在非稀疏数据的情况下，学习率过快衰减可能导致优化过程早期停滞。

AdaGrad是一种有效的自适应学习率算法，然而由于学习率衰减问题，我们会使用改 RMSProp 或 Adam 来替代。

示例：

     # 定义模型和损失函数
     model = torch.nn.Linear(10, 1)
     criterion = torch.nn.MSELoss()
     optimizer = torch.optim.Adagrad(model.parameters(), lr=0.01)
 
     # 模拟数据
     X = torch.randn(100, 10)
     y = torch.randn(100, 1)
 
     # 训练循环
     for epoch in range(100):
         optimizer.zero_grad()
         outputs = model(X)
         loss = criterion(outputs, y)
         loss.backward()
         optimizer.step()
         print(f'Epoch {epoch}, Loss: {loss.item()}')

2.4.4 RMSProp

虽然 AdaGrad 能够自适应地调整学习率，但随着训练进行，累积梯度平方 $G_t$ 会不断增大，导致学习率逐渐减小，最终可能变得过小，导致训练停滞。

RMSProp（Root Mean Square Propagation）是一种自适应学习率的优化算法，在时间步中，不是简单地累积所有梯度平方和，而是使用指数加权平均来逐步衰减过时的梯度信息。旨在解决 AdaGrad 学习率单调递减的问题。它通过引入 指数加权平均 来累积历史梯度的平方，从而动态调整学习率。

公式为：

$$
s_t=β⋅s_{t−1}+(1−β)⋅g_t^2\\θ_{t+1}=θ_t−\frac{η}{\sqrt{s_t+ϵ}}⋅gt
$$

其中：

$s_t$ 是当前时刻的指数加权平均梯度平方。
β是衰减因子，通常取 0.9。
η是初始学习率。
ϵ是一个小常数（通常取 $10^{-8}$ ），用于防止除零。
$g_t$ 是当前时刻的梯度。

优点

适应性强：RMSProp自适应调整每个参数的学习率，对于梯度变化较大的情况非常有效，使得优化过程更加平稳。
适合非稀疏数据：相比于AdaGrad，RMSProp更加适合处理非稀疏数据，因为它不会让学习率减小到几乎为零。
解决过度衰减问题：通过引入指数加权平均，RMSProp避免了AdaGrad中学习率过快衰减的问题，保持了学习率的稳定性

缺点

依赖于超参数的选择：RMSProp的效果对衰减率 $\gamma$ 和学习率 $\eta$ 的选择比较敏感，需要一些调参工作。

示例：

     # 定义模型和损失函数
     model = nn.Linear(10, 1)
     criterion = nn.MSELoss()
     optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01, alpha=0.9, eps=1e-8)
 
     # 模拟数据
     X = torch.randn(100, 10)
     y = torch.randn(100, 1)
 
     # 训练循环
     for epoch in range(100):
         optimizer.zero_grad()
         outputs = model(X)
         loss = criterion(outputs, y)
         loss.backward()
         optimizer.step()
         print(f'Epoch {epoch}, Loss: {loss.item():.4f}')

2.4.5 Adam

Adam（Adaptive Moment Estimation）算法将动量法和RMSProp的优点结合在一起：

动量法：通过一阶动量（即梯度的指数加权平均）来加速收敛，尤其是在有噪声或梯度稀疏的情况下。
RMSProp：通过二阶动量（即梯度平方的指数加权平均）来调整学习率，使得每个参数的学习率适应其梯度的变化。

Adam过程

初始化：
- 初始化参数 $\theta_0$ 和学习率 $\eta$ 。
- 初始化一阶动量估计 $m_0 = 0$ 和二阶动量估计 $v_0 = 0$ 。
- 设定动量项的衰减率 $\beta_1$ 和二阶动量项的衰减率 $\beta_2$ ，通常 $\beta_1$ = 0.9， $\beta_2$ = 0.999。
- 设定一个小常数 \epsilon（通常取 10^{-8}），用于防止除零错误。
梯度计算：
- 在每个时间步 t，计算损失函数 $J(\theta)$ 对参数 $\theta$ 的梯度 $g_t = \nabla_\theta J(\theta_t)$ 。
一阶动量估计（梯度的指数加权平均）：
- 更新一阶动量估计：
  
  $$
  m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t
  $$
  
  其中， $m_t$ 是当前时间步 t 的一阶动量估计，表示梯度的指数加权平均。
二阶动量估计（梯度平方的指数加权平均）：
- 更新二阶动量估计：
  
  $$
  v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2
  $$
  
  其中， $v_t$ 是当前时间步 t 的二阶动量估计，表示梯度平方的指数加权平均。
偏差校正：

由于一阶动量和二阶动量在初始阶段可能会有偏差，以二阶动量为例：

在计算指数加权平均时，初始化 $v_{0}=0$ ，那么 $v_{1}=0.999\cdot v_{0}+0.001\cdot g_{1}^2$ ，得到 $v_{1}=0.001\cdot g_{1}^2$ ，显然得到的 $v_{1}$ 会小很多，导致估计的不准确，以此类推：

根据： $v_{2}=0.999\cdot v_{1}+0.001\cdot g_{2}^2$ ，把 $v_{1}$ 带入后，得到： $v_{2}=0.999\cdot 0.001\cdot g_{1}^2+0.001\cdot g_{2}^2$ ，导致 $v_{2}$ 远小于 $g_{1}$ 和 $g_{2}$ ，所以 $v_{2}$ 并不能很好的估计出前两次训练的梯度。

所以这个估计是有偏差的。

使用以下公式进行偏差校正：

$$
\hat{m}_t = \frac{m_t}{1 - \beta_1^t} \\ \hat{v}_t = \frac{v_t}{1 - \beta_2^t}
$$

其中， $\hat{m}_t$ 和 $\hat{v}_t$ 是校正后的一阶和二阶动量估计。

推导：

假设梯度 ${g_t}$ 是一个平稳的随机变量，其期望为：

$$
E(g_t)=μ
$$

根据指数加权平均的递推公式，我们可以递推计算 ${m_t}$ 的期望。

当t=1：

$$
m_1=β⋅m_0+(1−β)⋅g_1
$$

假设 $m_0=0$ ，所以：

$$
m_1=(1−β)⋅g_1
$$

取期望：

$$
E(m1)=(1−β)⋅E(g_1)=(1−β)⋅μ
$$

当t=2：

$$
m_2=β⋅m_1+(1−β)⋅g_2
$$

代入 $m_1 = (1-\beta )\cdot g_1$ ：

$$
m_2=β⋅(1−β)⋅g_1+(1−β)⋅g_2
$$

取期望：

$$
E(m_2)=β⋅(1−β)⋅E(g_1)+(1−β)⋅E(g_2)=β(1−β)⋅μ+(1−β)⋅μ=(1−β^2)⋅μ
$$

当t=3：

$$
m_3=β⋅m_2+(1−β)⋅g_3
$$

代入 $m_2=\beta (1-\beta )\cdot g_1+(1-\beta )\cdot g_2$ ：

$$
m_3=β⋅[β(1−β)⋅g_1+(1−β)⋅g_2]+(1−β)⋅g_3
$$

展开：

$$
m_3=β^2(1−β)⋅g_1+β(1−β)⋅g_2+(1−β)⋅g_3
$$

取期望：

$$
E(m_3)=β^2(1−β)⋅μ+β(1−β)⋅μ+(1−β)⋅μ=(1−β^3)⋅μ
$$

通过递推可以发现，对于任意时刻 t， $m_t$ 的期望为：

$$
E(m_t)=(1−β^t)⋅μ
$$

通过上述公式我们发现m_t的期望与梯度期望相差了 $(1-\beta ^t)$ 倍，我们想要找到一个修正后的 $\hat{m_t}$ ，使： $E(\hat{m_t})=\mu$

所以：

$$
E(m_t)=(1−β^t)⋅μ=(1−β^t)⋅E(\hat{m_t})
$$

进行缩放：

$$
m_t=(1−β^t)⋅\hat{m_t}
$$

得出：

$$
\hat{m_t}=\frac{m_t}{1−β^t}
$$

$v_t$ 推导同理。
参数更新：
- 使用校正后的动量估计更新参数：
  
  $$
  \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t
  $$

优点

高效稳健：Adam结合了动量法和RMSProp的优势，在处理非静态、稀疏梯度和噪声数据时表现出色，能够快速稳定地收敛。
自适应学习率：Adam通过一阶和二阶动量的估计，自适应调整每个参数的学习率，避免了全局学习率设定不合适的问题。
适用大多数问题：Adam几乎可以在不调整超参数的情况下应用于各种深度学习模型，表现良好。

缺点

超参数敏感：尽管Adam通常能很好地工作，但它对初始超参数（如 $\beta_1$ 、 $\beta_2$ 和 $\eta$ ）仍然较为敏感，有时需要仔细调参。
过拟合风险：由于Adam会在初始阶段快速收敛，可能导致模型陷入局部最优甚至过拟合。因此，有时会结合其他优化算法（如SGD）使用。

2.5 总结

梯度下降算法通过不断更新参数来最小化损失函数，是反向传播算法中计算权重调整的基础。在实际应用中，根据数据的规模和计算资源的情况，选择合适的梯度下降方式（批量、随机、小批量）及其变种（如动量法、Adam等）可以显著提高模型训练的效率和效果。

Adam是目前最为流行的优化算法之一，因其稳定性和高效性，广泛应用于各种深度学习模型的训练中。Adam结合了动量法和RMSProp的优点，能够在不同情况下自适应调整学习率，并提供快速且稳定的收敛表现。

示例：

     # 定义模型和损失函数
     model = nn.Linear(10, 1)
     criterion = nn.MSELoss()
     optimizer = torch.optim.Adam(model.parameters(), lr=0.01, betas=(0.9, 0.999), eps=1e-8)
 
     # 模拟数据
     X = torch.randn(100, 10)
     y = torch.randn(100, 1)
 
     # 训练循环
     for epoch in range(100):
         optimizer.zero_grad()
         outputs = model(X)
         loss = criterion(outputs, y)
         loss.backward()
         optimizer.step()
         print(f'Epoch {epoch}, Loss: {loss.item():.4f}')