代码随想录算法训练营Day9 | 232. 用栈实现队列，225. 用队列实现栈，20. 有效的括号，1047. 删除字符串中的所有相邻重复项

目录

232. 用栈实现队列

225. 用队列实现栈

20. 有效的括号

1047. 删除字符串中的所有相邻重复项

---

232. 用栈实现队列

题目链接：232. 用栈实现队列 - 力扣（LeetCode）

文章讲解：代码随想录

解题卡点：双栈实现队列的pop逻辑不清晰

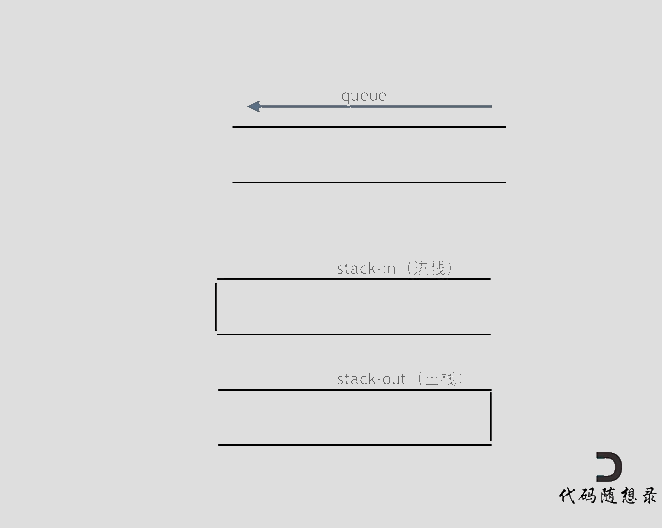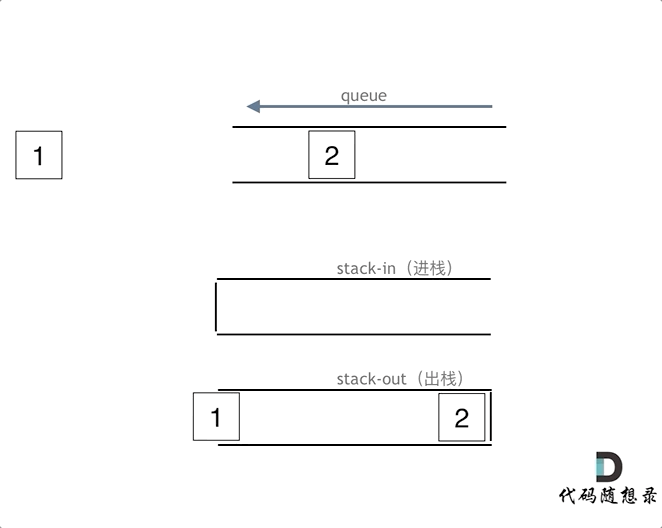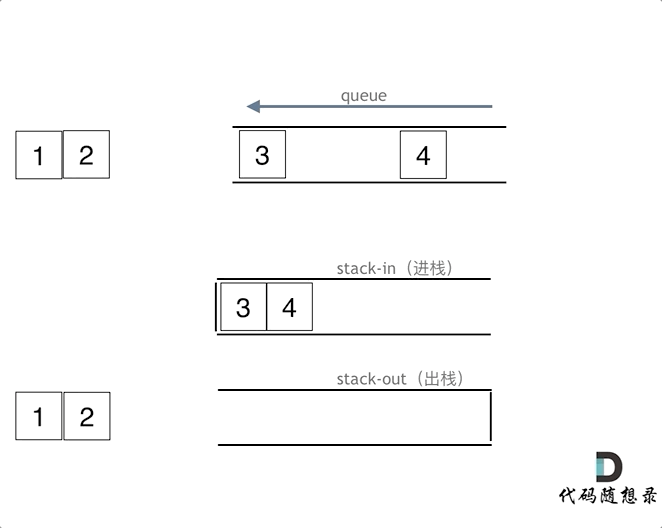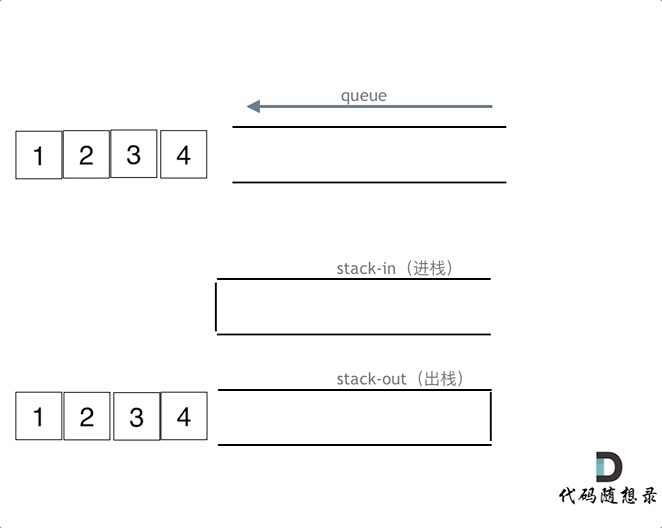
        使用栈模拟队列需要2个栈，一个输入栈，一个输出栈。在push时，只需将数据添加进输入栈。而在pop时，若输出栈为空，则将输入栈全部数据导入输出栈，再从输出栈弹出数据。若输出栈不为空，直接弹出数据。

        Tips：

        peek与pop的功能相似，可以直接复制粘贴代码么？

        不能。在工业级别代码开发中，最忌讳的就是实现一个类似的函数，直接把代码粘过来改一改。这样的项目代码会越来越乱。一定要懂得复用，功能相近的函数要抽象出来，不要大量的复制粘贴，很容易出问题。

class MyQueue:

    def __init__(self):
        self.stack_in = []
        self.stack_out = []

    def push(self, x: int) -> None:
        self.stack_in.append(x)

    def pop(self) -> int:
        if not self.stack_out: # 当stack_out中没有元素时
            while self.stack_in: # 将stack_in中元素全部放入out，实现顺序的调转
                self.stack_out.append(self.stack_in.pop())
        return self.stack_out.pop()

    def peek(self) -> int:
        res = self.pop() # 重复利用函数
        self.stack_out.append(res) # 从stack_out中弹出了元素，由于是peek，故再补上该元素
        return res

    def empty(self) -> bool:
        return (not self.stack_in) and (not self.stack_out) # stack_in和stack_out均为空时，整体队列为空

    # 时间复杂度 O(1)
    # 空间复杂度 O(n)

---

225. 用队列实现栈

题目链接：225. 用队列实现栈 - 力扣（LeetCode）

文章讲解：代码随想录

解题卡点：想到循环队列元素就好

        两个队列模拟：把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1。

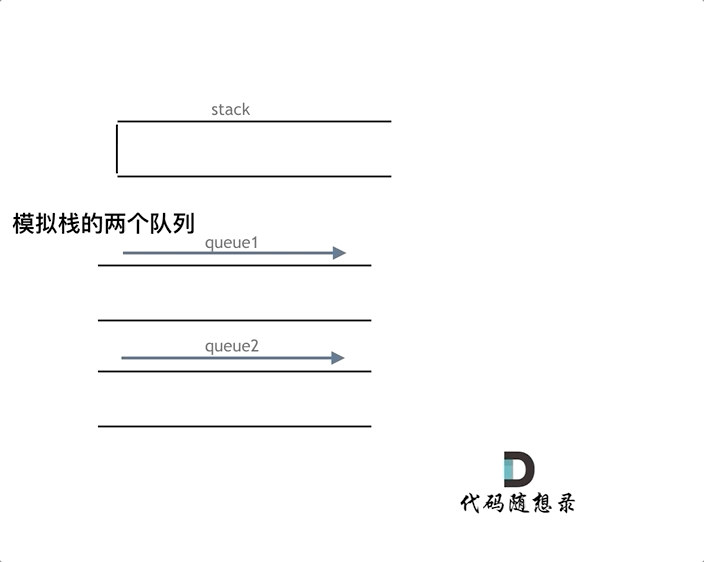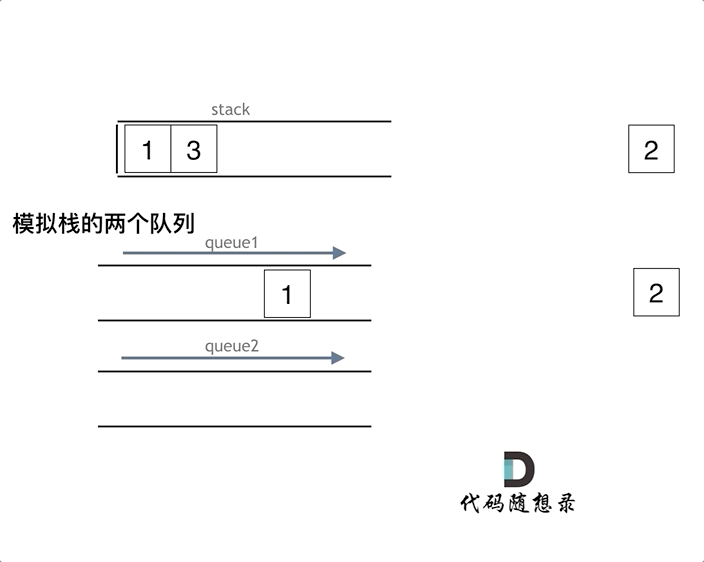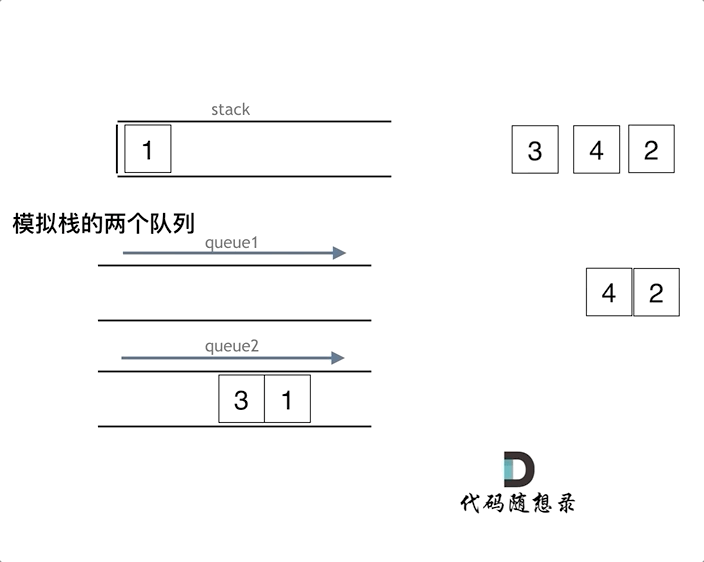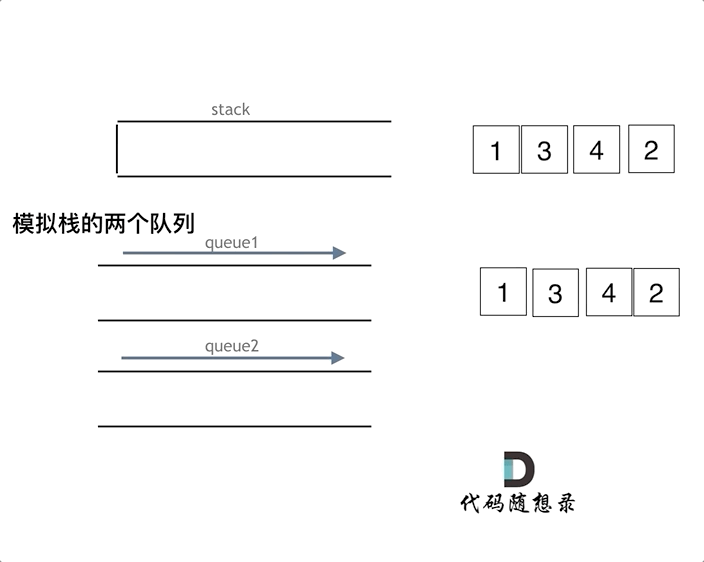
        一个队列模拟：在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

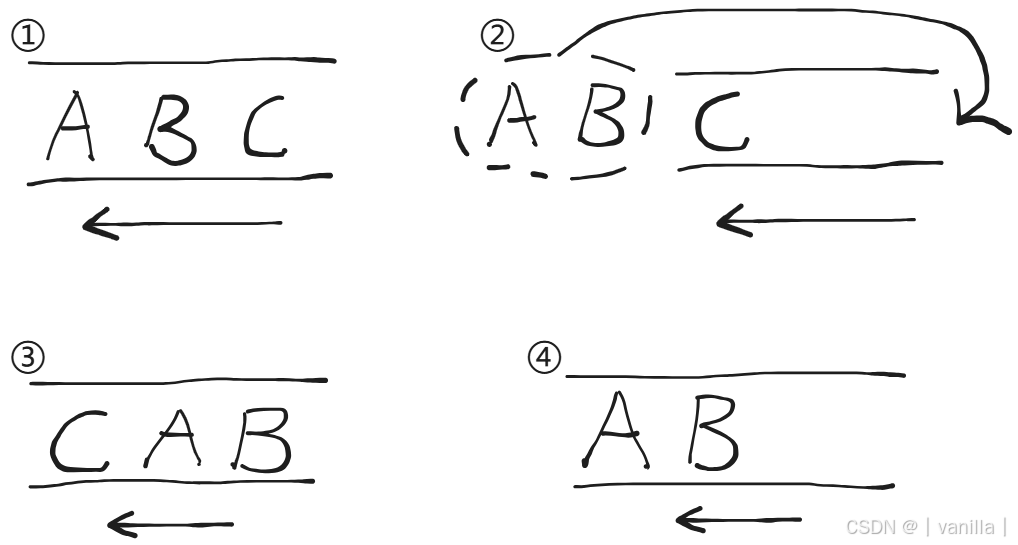
class MyStack:

    def __init__(self): # list.pop(0)的时间复杂度为O(n)
        self.queue = [] # 可使用双向队列deque()，弹出的时间复杂度为O(1)

    def push(self, x: int) -> None:
        self.queue.append(x)

    def pop(self) -> int:
        i = 0
        while i < len(self.queue)-1: # 将除队尾元素依次重新入队
            temp = self.queue.pop(0)
            self.queue.append(temp)
            i += 1
        return self.queue.pop(0) # 此时队尾元素在新队列最前面，弹出

    def top(self) -> int:
        res = self.pop()
        self.queue.append(res) # top函数不改变元素位置，经过pop后队尾元素置顶了，故再重新加入队尾恢复原本的顺序
        return res

    def empty(self) -> bool:
        return not self.queue

    # 时间复杂度 O(1)，pop和top为O(n)
    # 空间复杂度 O(n)

---

20. 有效的括号

题目链接：20. 有效的括号 - 力扣（LeetCode）

文章讲解：代码随想录

解题卡点：三种不匹配情况没想清楚

        由于栈结构的特殊性，非常适合做对称匹配类的题目。

        该题首先要想清楚括号不匹配有几种情况，不然会修修补补越写越乱。想清楚以下三种情况就好写。

        情况①：左括号多余，没有相应的右括号来匹配；

        情况②：左括号和右括号匹配错误；

        情况③：左右括号匹配完毕，但还多出来右括号未能匹配。

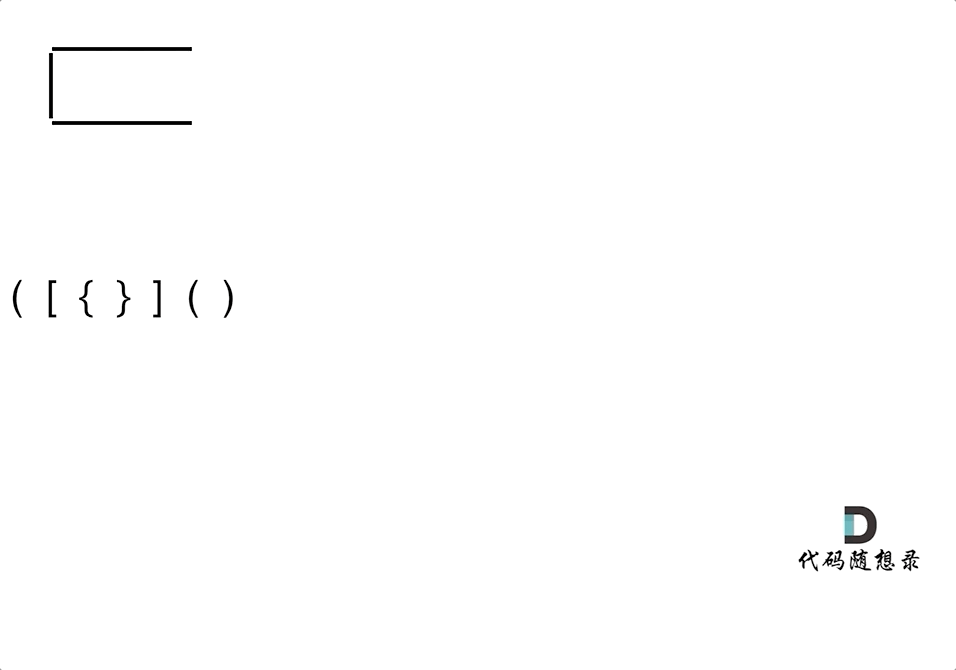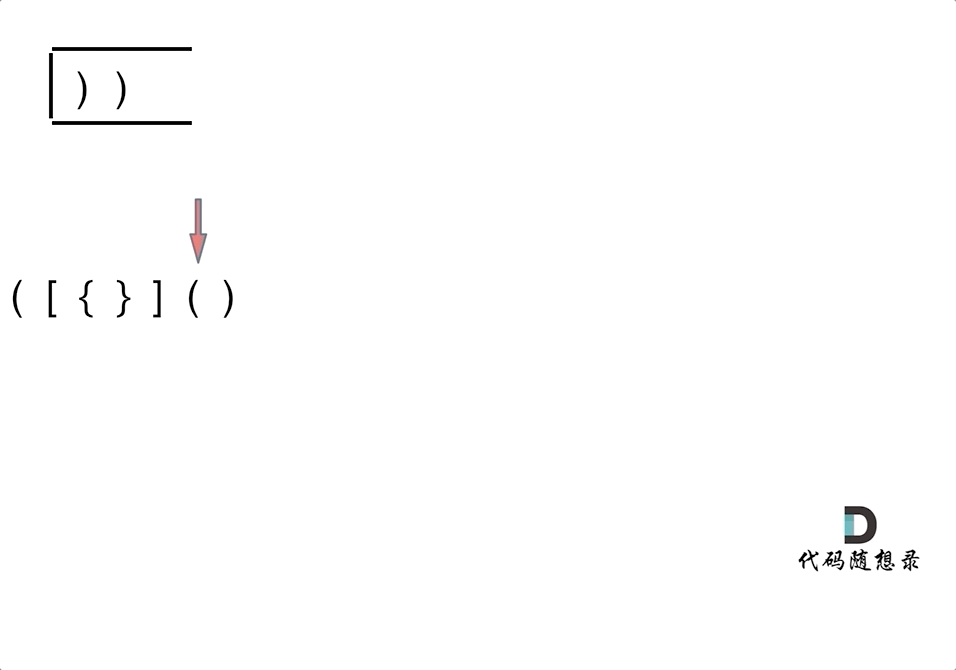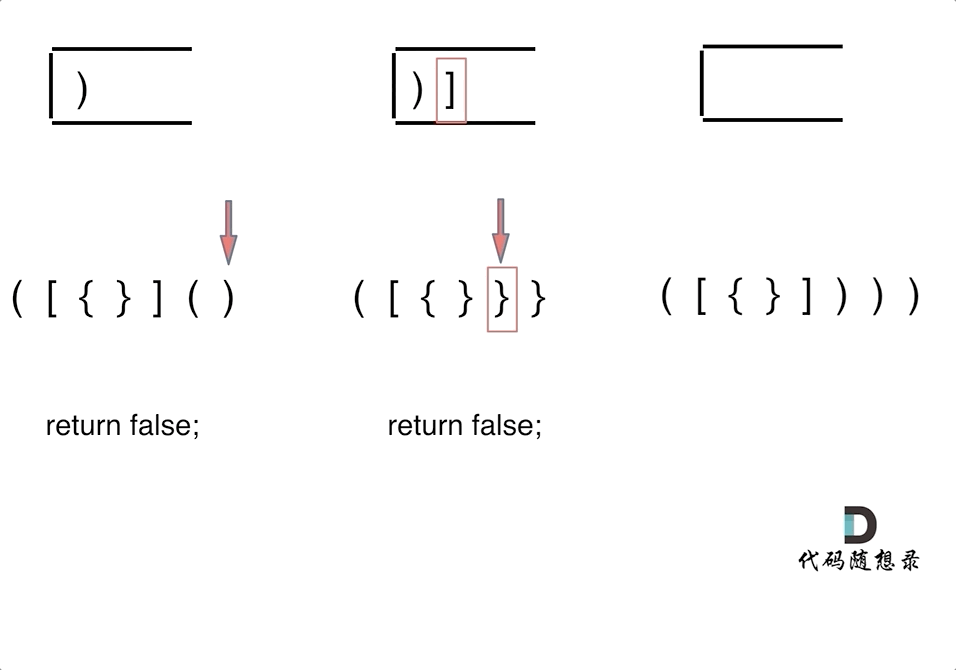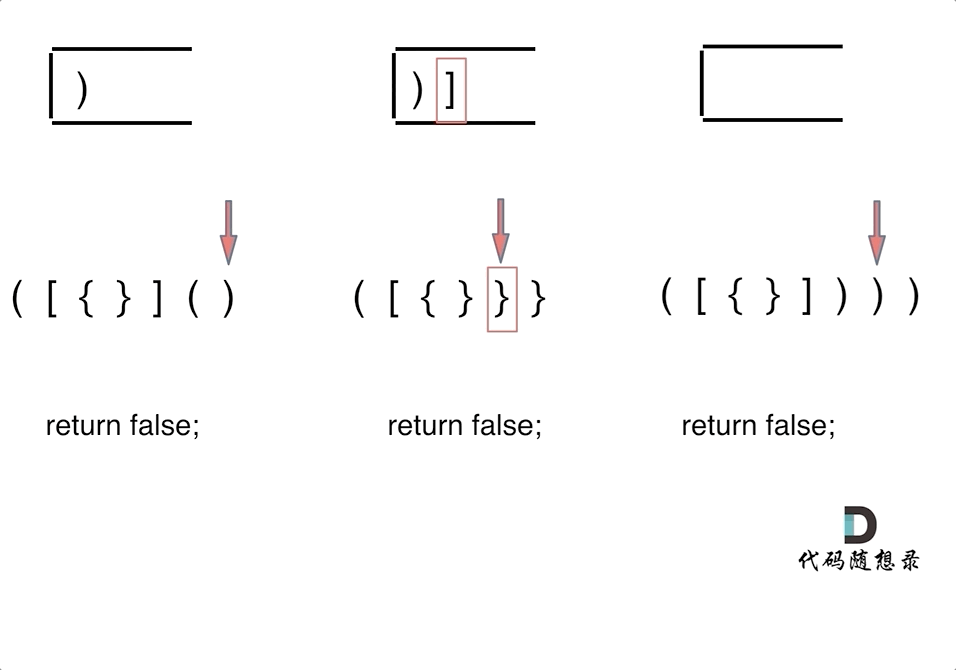
        小技巧，在匹配左括号的时候，将对应的右括号入栈，这样在遇见右括号时，就只需要比较当前元素和栈顶相不相等就可以了，比左括号入栈代码实现要简单。

# 左括号入栈
class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        left = '([{'
        right = ')]}'
        for i in s:
            if i in left:
                stack.append(i)
            else:
                if stack == []:
                    return False # 情况3
                if left.index(stack[-1]) != right.index(i):
                    return False # 情况2
                stack.pop()
        return True if stack==[] else False # 情况1

# 右括号入栈
class Solution:
    def isValid(self, s: str) -> bool:
        stack = []       
        for item in s:
            if item == '(':
                stack.append(')')
            elif item == '[':
                stack.append(']')
            elif item == '{':
                stack.append('}')
            elif not stack or stack[-1] != item: # 情况23
                return False
            else:
                stack.pop()      
        return True if not stack else False # 情况1

    # 时间复杂度 O(n)
    # 空间复杂度 O(n)

---

1047. 删除字符串中的所有相邻重复项

题目链接：1047. 删除字符串中的所有相邻重复项 - 力扣（LeetCode）

文章讲解：代码随想录

解题卡点：对-1进行索引可能报错

        匹配相邻元素，完成消除操作→栈。为什么栈适合做匹配消除呢？因为栈帮助我们记录了遍历数组当前元素时，前一个元素是什么。

        解题方式类似于20. 有效的括号。

        Tips：

        使用not stack or i != stack[-1]，以避免索引-1报错。在初始状态，stack为[]，not stack为True，有一个True则整个or的判断都为True。因此跳过了i != stack[-1]的判断，避免了-1越界。

# 给栈额外加上' '避免索引-1报错，但后续[1:]会多遍历一次stack
class Solution:
    def removeDuplicates(self, s: str) -> str:
        stack = [' ']
        for i in s:
            if i != stack[-1]:
                stack.append(i)
            else:
                stack.pop()
        return ''.join(stack[1:])

# 利用or的两边，有一个True就整个True的性质，避免了额外加' '
class Solution:
    def removeDuplicates(self, s: str) -> str:
        stack = []
        for i in s:
            if not stack or i != stack[-1]:
                stack.append(i)
            else:
                stack.pop()
        return ''.join(stack)

    # 时间复杂度 O(n)
    # 空间复杂度 O(1)