目录
209. 长度最小的子数组
题目链接:. - 力扣(LeetCode)
文章讲解:代码随想录
解题卡点: 无
双指针法&滑动窗口:左右指针的窗口内即为连续数组。窗口数组的和大于等于目标值,左指针向前移动,窗口缩小,窗口数组的值缩小;窗口数组的和小于目标值,右指针向前移动,窗口增大,窗口数组的值增大。不断更新窗口数组和大于等于目标值的数组长度,遍历结束后得到最小数组长度。
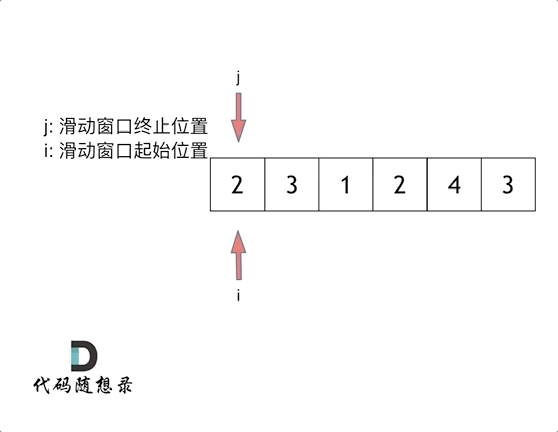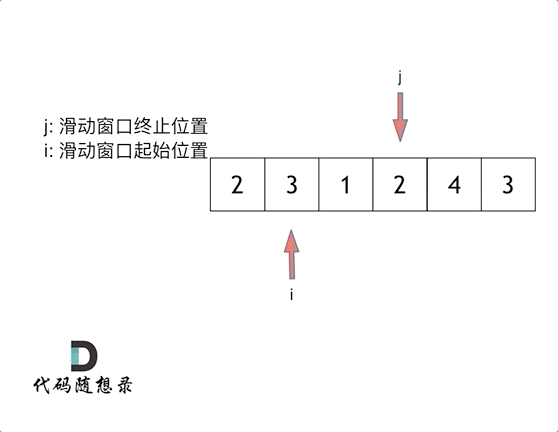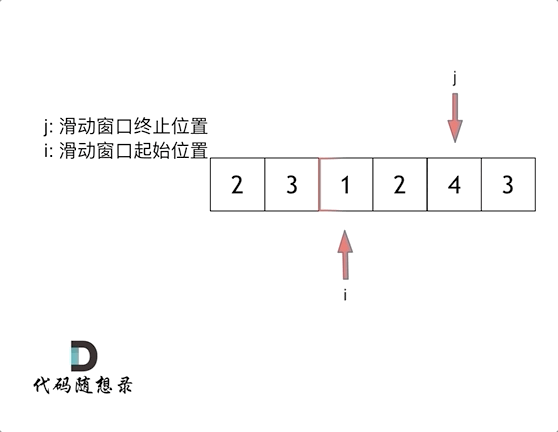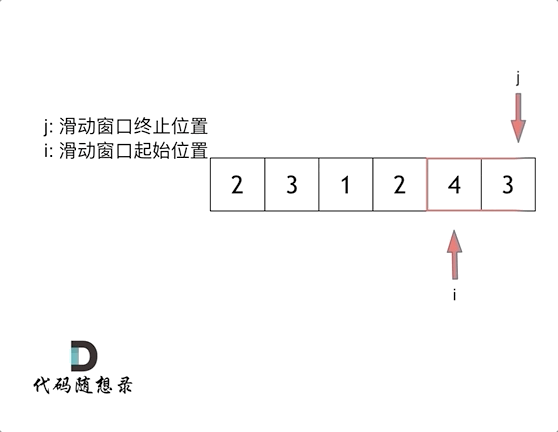
做题时可以先固定移动右指针,判断条件收缩左指针。这里使用for循环控制右指针,循环结束一次右指针+1,因此在循环内专心控制左指针就行。当窗口数组和大于等于目标值时,记录窗口长度,减去该元素,左指针+1.
总结: 涉及连续子数组的问题,通常有两种思路:一是滑动窗口、二是前缀和。滑动窗口得益于元素非负,右指针向右一定增加总和,左指针向右一定减少总和。若数组含有负元素,不可使用该方法,因为有负数的话无论是收缩还是扩张窗口,窗口内值的总和可能增加也可能减少,不像之前收缩一定变小,扩张一定变大。
Tips:
①窗口的数字和使用累积和cum_sum来计算,比sum(list)快。cum_sum的右指针+1数组和就加该元素值,左指针+1就减该元素值,而sum会遍历整个子数组。
②时间复杂度O(n)。时间复杂度看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,故时间复杂度是2×n,也就是O(n)。
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
sub_len = float('inf') # 数组长度初始值,设为无穷大
sub_sum = 0 # 数组和
left = 0 # 左指针
for right in range(len(nums)): # 右指针使用for循环自动进行
sub_sum += nums[right] # 累加右指针元素
while sub_sum >= target:
sub_len = min(right-left+1, sub_len) # 不断更新满足条件窗口数组的最小长度
sub_sum -= nums[left] # 累减左指针元素
left += 1
if sub_len == float('inf'): # 没有满足条件的窗口数组时特殊处理
sub_len = 0
return sub_len
# 时间复杂度 O(n)
# 空间复杂度 O(1)59. 螺旋矩阵II
题目链接:. - 力扣(LeetCode)
文章讲解:代码随想录
解题卡点:循环规律是什么
过程模拟题,考察对代码的掌控能力。
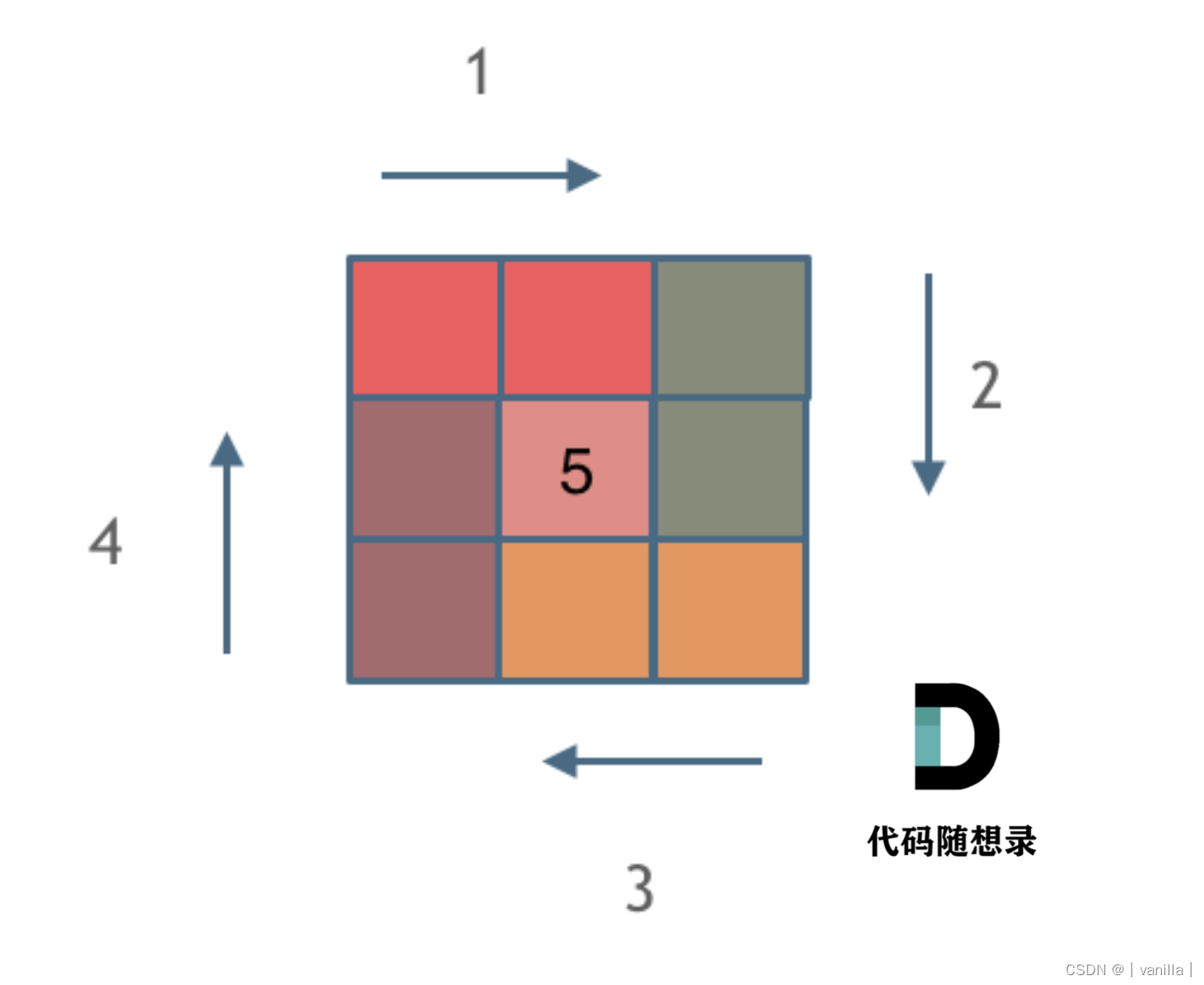
本题重点在于坚持循环不变量。我一开始的想法是,从外围顺时针按3、2、2、1的个数填充。然而个数不一样,写循环的代码困难重重。因此应该坚持个数不变,如上图,从外围顺时针按2、2、2、2的个数填充,保证每个循环都相同。另外最外层填充完,填充倒数第二圈时,每圈起始索引list[0][0]应该变成list[1][1],同时每个方向填充的个数也要少2个。这些变化使用offest控制,代表每一圈上述变化的偏移量。
总结:坚持循环不变量,找到规律,注意偏移量,由外向内一圈一圈填充。
Tips:
①对于n为奇数的矩阵来说,正中心是一个数而不是一个圈。可以对这种情况单独处理,使矩阵中心为n^2。也可以在创建矩阵时,使所有元素均为n^2,不用再单独处理。
②关于初始数组的创建,以n=3为例,对初始数组matrix_1的中心赋值,数组全部元素均发生变化。
matrix_1 = [[0] * 3] * 3
matrix_2 = [[0] * 3 for _ in range(3)]
matrix_3 = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
print('', matrix_1, '\n', matrix_2, '\n', matrix_3)
# [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
# [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
# [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
matrix_1[1][1] = 9
matrix_2[1][1] = 9
matrix_3[1][1] = 9
print('', matrix_1, '\n', matrix_2, '\n', matrix_3)
# [[0, 9, 0], [0, 9, 0], [0, 9, 0]]
# [[0, 0, 0], [0, 9, 0], [0, 0, 0]]
# [[0, 0, 0], [0, 9, 0], [0, 0, 0]]原因如下:

参考来源:Python数据结构与算法分析(第三版),p9
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
res = [[n**2]*n for _ in range(n)] # 初始数组
offest = 0 # 每条边遍历长度的偏移量
val = 1 # 待填充的数值
loop = n//2 # 循环圈数
col = 0 # 填充列索引
row = 0 # 填充行索引
while loop: # 只要循环圈数没归0就继续下去
boundary = n-offest-2 # 每条边本圈可填充的数量,以3为例这里是1
while col <= boundary: # 向右填充,列索引取值0、1
res[row][col] = val
val += 1
col += 1
while row <= boundary: # 向下填充
res[row][col] = val
val += 1
row += 1
while n-col-1 <= boundary: # 向左填充
res[row][col] = val
val += 1
col -= 1
while n-row-1 <= boundary: # 向上填充
res[row][col] = val
val += 1
row -= 1
col += 1 # 每圈起始值向右下角移动
row += 1 # 每圈起始值向右下角移动
offest += 1
loop -= 1 # 本圈填充结束,圈数-1
return res
# 时间复杂度 O(n^2)
# 空间复杂度 O(1)Kama58. 区间和
题目链接:58. 区间和(第九期模拟笔试)
文章讲解:58. 区间和 | 代码随想录
解题卡点:不熟悉ACM模式
前缀和:重复利用计算过的子数组之和,降低区间查询需要累加计算的次数。前缀和在涉及区间和的问题时非常有用。
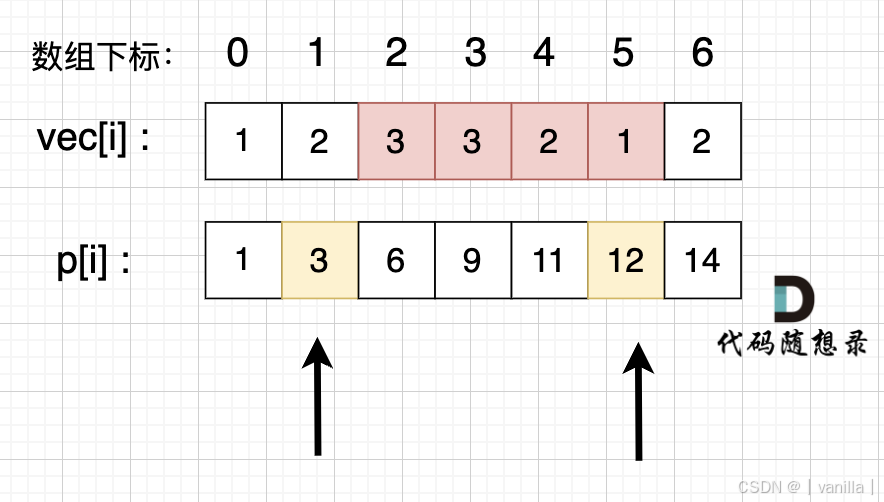
计算区间2~5的和时,只需用5的前缀和减去1的前缀和。在解题时注意顺序,先构造前缀和初始化列表,再通过对应下标值相减得到区间和。
Tips:
sys.stdin.read()会将所有输入内容一次性读取,包括换行符等内容。input()会按行读取输入内容,不会包括换行符。
#以下面输入为例
#5
#1
#2
#3
#4
#5
#0 1
#1 3
import sys
input = sys.stdin.read() # str'5\n1\n2\n3\n4\n5\n0 1\n1 3\n'
def main():
data = input.split() # list['5','1','2','3','4','5','0','1','1','3']
data = list(map(int, data)) # list[5, 1, 2, 3, 4, 5, 0, 1, 1, 3]
array_len = data[0]
p = [] # 前缀和数组初始化
cum_sum = 0
for i in range(1, array_len+1):
cum_sum += data[i]
p.append(cum_sum) # p = [1, 3, 6, 10, 15]
idx = array_len + 1 # 按批次将输入数组后面的待求区间信息传入a和b
while idx <= len(data)-1:
a = data[idx]
b = data[idx+1]
if a == 0:
sub_sum = p[b]
else:
sub_sum = p[b] - p[a-1]
print(sub_sum) # ACM模式使用print输出
idx += 2
if __name__ == '__main__':
main()Kama44. 开发商购买土地
题目链接:44. 开发商购买土地(第五期模拟笔试)
文章讲解:44. 开发商购买土地 | 代码随想录
解题卡点:从一维前缀和转为二维有点懵
首先要理解题目。本题为创建一个矩阵,对矩阵进行一次横向分割,或者一次纵向分割,得到两个小矩阵,计算两个小矩阵的内部和,并得到它们的差值。遍历每一种切法,输出最小的差值。
二维区间和计算→二维前缀和。二维前缀和初始化与求值公式如下:
class MatrixSum:
def __init__(self, matrix: List[List[int]]):
m, n = len(matrix), len(matrix[0])
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(matrix):
for j, x in enumerate(row):
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + x
self.s = s
# 返回左上角在 (r1,c1) 右下角在 (r2-1,c2-1) 的子矩阵元素和(类似前缀和的左闭右开)
def query(self, r1: int, c1: int, r2: int, c2: int) -> int:
return self.s[r2][c2] - self.s[r2][c1] - self.s[r1][c2] + self.s[r1][c1]
# 如果你不习惯左闭右开,也可以这样写
# 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
def query2(self, r1: int, c1: int, r2: int, c2: int) -> int:
return self.s[r2 + 1][c2 + 1] - self.s[r2 + 1][c1] - self.s[r1][c2 + 1] + self.s[r1][c1]
#作者:灵茶山艾府
#链接:https://leetcode.cn/circle/discuss/UUuRex/在本题中,由于直上直下分割,待求和小矩阵的左上角点始终为(0, 0)。
#以下面输入为例
#3 4
#1 2 3 8
#2 1 3 12
#1 2 3 3
import sys
input = sys.stdin.read()
def main():
data = input.split()
data = list(map(int, data)) # [3,4,1,2,3,8,2,1,3,12,1,2,3,3]
m, n = data[0], data[1] # 得到矩阵的行列数
res = float('inf')
matrix = [] # 将输入转为标准的矩阵形式
val_idx = 2
while val_idx <= len(data)-1:
row = []
col_idx = 1
while col_idx <= n:
row.append(data[val_idx])
col_idx += 1
val_idx += 1
matrix.append(row) # matrix[[1,2,3,8], [2,1,3,12], [1,2,3,3]]
p = [[0]*(n+1) for _ in range(m+1)] # 二维前缀和矩阵
for i, row in enumerate(matrix):
for j, x in enumerate(row):
p[i+1][j+1] = p[i+1][j] + p[i][j+1] - p[i][j] + x
#前缀和初始化矩阵p
#0 0 0 0 0
#0 1 3 6 14
#0 3 6 12 32
#0 4 9 18 41
total_sum = p[-1][-1] # 输入矩阵的总和
for i in range(0, n-1): # 按列遍历(竖着切矩阵,第一次切完为1,2,1)
sub_sum = p[m][i+1] # 对应在p上就是最下面一行第二列的4
res = min(res, abs(sub_sum - (total_sum - sub_sum)))
for i in range(0, m-1): # 按行遍历
sub_sum = p[i+1][n]
res = min(res, abs(sub_sum - (total_sum - sub_sum)))
print(res)
if __name__ == '__main__':
main()




















 1420
1420

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








