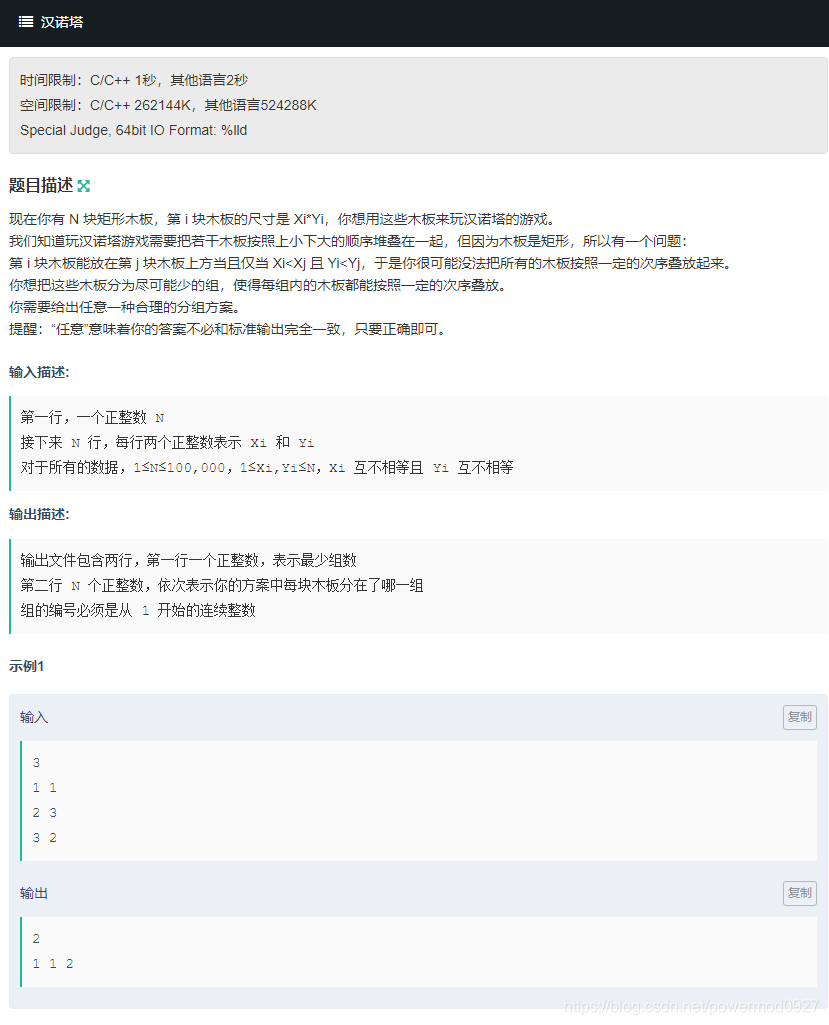
2020牛客寒假算法基础集训营6-汉诺塔

最新推荐文章于 2020-04-09 00:21:47 发布

岛屿失梦°

最新推荐文章于 2020-04-09 00:21:47 发布

阅读量243

点赞数

CC 4.0 BY-SA版权

分类专栏：牛客补题

本文链接：https://blog.youkuaiyun.com/powermod0927/article/details/104725083

牛客补题专栏收录该内容

10 篇文章

订阅专栏

本文深入探讨了Dilworth定理在算法优化中的应用，特别是在链划分和反链划分的问题上，通过实例解析如何使用该定理来减少集合数。同时，文章提供了详细的代码实现，包括G++优化技巧和数据结构操作，如链表和哈希表的高效使用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2020牛客寒假算法基础集训营6-汉诺塔

好题
Dilworth定理
U的链划分使用的最少集合数，等于它的最大反链长度。（1）
U的反链划分使用的最少集合数，等于它的最大链长度。（2）
在这里插入图片描述

#pragma GCC optimize(3,"Ofast","inline")    //G++
#include<bits/stdc++.h>
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define fcout cout<<setprecision(4)<<fixed
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;


const int inf=0x3f3f3f3f;
const ll INF=0x7fffffffffffffff;
const int mod=1e9+7;
const int maxn = 1e6+5;
const double eps=1e-8;

template<typename T> void read(T &x){
    x = 0;char ch = getchar();ll f = 1;
    while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
    while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
template<typename T, typename... Args> void read(T &first, Args& ... args) {
    read(first);
    read(args...);
}
int sgn(double a){
    return a<-eps?-1:a<eps?0:1;
}

int n,a[maxn],dp[maxn],ans,pos[maxn],mp[maxn];
pair<int,int>p[maxn];
void solve(){
    read(n);
    for(int i=1;i<=n;i++){
        read(p[i].first,p[i].second);
        pos[i]=p[i].second;
    }
    sort(p+1,p+n+1);
    for(int i=1;i<=n;i++){
        a[i]=p[i].second;
    }
    ans=1;
    dp[1]=a[1];
    mp[a[1]]=1;
    for(int i=2;i<=n;i++){
        if(a[i]<dp[ans]){
            dp[++ans]=a[i];
            mp[a[i]]=ans;
        }
        else{
            int pos=upper_bound(dp+1,dp+ans+1,a[i],greater<int>())-dp;
            dp[pos]=a[i];
            mp[a[i]]=pos;
        } 
    }
    cout<<ans<<"\n";
    for(int i=1;i<=n;i++){
        cout<<mp[pos[i]]<<" ";
    }
    cout<<"\n";
}
int main(){
    solve();
}

好题！！！！