96.不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

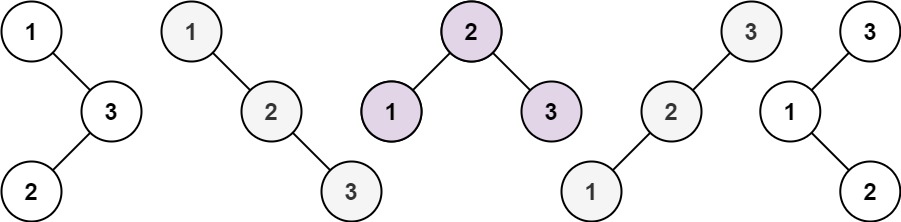
输入：n = 3
输出：5

思路：

对于n个节点而言，可以以1-n中任意元素j为根节点

根节点左侧的二叉搜索树元素均小于j，数量为j-1个，树的形状有dp[j-1]种可能性。

同理右侧左侧的二叉搜索树元素均大于j，数量为i-j个，树的形状为dp[i-j]个。

根据排列组合的原理，对于每一个以j为根节点的二叉搜索树，有$dp[j-1]\ast dp[i-j]$种排列。

因此递推公式为：
$$\begin{gathered} dp[i]+=dp[j-1]\ast dp[i-j] \\ dp[i]表示i个节点的二叉搜索树的种数 \end{gathered}$$
代码：

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1);
        dp[0]=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
};