前言:
近日帮同学处理了一下数学建模里面的问题,涉及到路径选择,由此产生了两个想法,在此记录一下。问题简述:给定12个城市,给出每个城市的网络容量C和任意两个城市的距离D,由此可求出任意两个城市的网络通信价值V。以城市(名)为节点,网络通信价值V为权重,可得网络通信价值图。要求找出16条路径,需满足两个约束:1,这16条路径需包含所有城市(节点);2,在满足条件1 的同时要求这些路径的通信价值和最大。其实暗含了第三个约束,同一城市对不允许重复出现。假设1号城市到5号城市的通信价值最大,那么5号城市到1号城市的价值自然也最大,那么路径(1,5)和(5,1)都被选中就没有必要了,只选一个就好。
正文:
先将此问题抽象为一个m乘m(有12 个城市,这里m=12)的矩阵,每个元素即为其横纵坐标(两个城市)对应的网络通信价值。接下来我们要做的就是从这个矩阵中选出16个点,满足:1,这16个点涵盖所有坐标(序号1~12);2,在满足1的同时,这些点的值加起来最大。
先来浅析一波,一共就要满足两个约束,无非就是先满足全覆盖节点再保证代价和最大,或者先保证代价和最大再满足全节点覆盖。强调一下,由于横纵坐标都是这些城市,所以这是一个对角线为0的对称矩阵。根据矩阵点元素代表的意义不同,有时候对角线不一定是0,但是对称矩阵这一点基本不变。再说一遍,对称矩阵!
方案一:先覆盖全部节点,再保障这些节点代价和最大。
方法如下:1,对矩阵的每列降序排序,即这一列从上往下看数值递减。2,虽然第一行的数值对于每一列来说都是该列最大值,但是这些值有可能是相等的,就是对称矩阵导致的这个现象。3,第一行出现相等值时需要将其中一个换下,比较这两列的第二行(其实就是次大值),选择次大值较大的那列操作。将被操作列的第一行元素加入列尾,原倒数第一行至正数第二行元素整体上升一行。就是该列最大值放到最下面,其他值依次上升。因为要保证代价和最大,所以替换上来的值要尽可能大,因此选择次大值较大的那列操作。被向下替换的数值已经失去价值,不参与第5步的过程。调整后可能产生新的相等列,先不管,放到下一轮处理。4,对第一行调整后可能产生新的相等列,回到第3步。若第一行没有相等列,进入第5步。5,在余下的所有点中选择最大的4个点,这4个点不包含失效点。当然,也没有相等点。
那么,如何能说明这样做是合适的呢?方案一的核心思想就是找到一条包含12个城市的最大通信代价路径,之后再从剩下的点钟选最大的四点。不难看出,无论怎么调整第一行的点都被选中时,可以保证节点全覆盖。接下来需要保证这12个点是通信代价和最大的。利用反证法,证明第一行每一个点都是不可替换的就行。以下是一个演示过程,四个城市选择6条路径。
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 500 | 400 | 100 |
| 2 | 500 | 0 | 300 | 200 |
| 3 | 400 | 300 | 0 | 600 |
| 4 | 100 | 200 | 600 | 0 |
| 1 | 2 | 3 | 4 | |
| 1 | 500 | 500 | 600 | 600 |
| 2 | 400 | 300 | 400 | 200 |
| 3 | 100 | 200 | 300 | 100 |
| 4 | 0 | 0 | 0 | 0 |
第一行出现相等值,1列和2列相等,3列和4列相等,需要调整。
| 1 | 2 | 3 | 4 | |
| 1 | 400 | 500 | 400 | 600 |
| 2 | 100 | 300 | 300 | 200 |
| 3 | 0 | 200 | 0 | 100 |
| 4 | 500 | 0 | 600 | 0 |
第一行再次出现相等值,第1列和第3列相等,继续调整。
| 1 | 2 | 3 | 4 | |
| 1 | 400 | 500 | 300 | 600 |
| 2 | 100 | 300 | 0 | 200 |
| 3 | 0 | 200 | 600 | 100 |
| 4 | 500 | 0 | 400 | 0 |
此时,第一行没有相等列了。再从剩下的点里面选两个最大的。坐标(2,2)对应的300 最大,但是不选,因为第一行出现过300(1,3)。第二行的100(2,1)和200(2,4)可取。上图即为最终状态。
现在来说明第一行的点为什么不能被替代。不难看出,第一行的点也有较小的值(这里极差不明显),可能会想到这样的点能不能换成更大的值呢?很遗憾,答案是不能!以第3列为例,确实有比300大的点,但是它们在之前的优化选择中已经被替换下去,不是所需的点。第3列可取的点里面300已经最大了。现在,已经说明了第一行的各列不会被本列的其他值替代。可是,每个点包含两个坐标(城市),那么这个点含有的两个坐标(城市)有没有可能被别的两个点(最多包含四个城市)替代?以上述表格数据为例,我们假设(第一行)某个点Sr可以被其他两个点S1和S2替代。记所需的六个点的总和为St,可替代的个例点记为Sr,第一行的点之和记为Sf,第一行除个例点之外的点之和记为So。除第一行的点之外还要从剩下的点中选取两个最大的点,记为Top2。
![]()
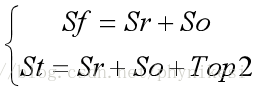
假设被替代Sr的坐标是(m,n),取代者分别为S1(p,m)和S2(q,n),因为是对称矩阵,用S1(m,p)和(n,q)也是一样的。S1暂且不论,先看S2。S2(q,n)的值必然来自第n列,当前点Sr(m,n)的值已经是该列(可取点的值)最大,所以S2<=Sr。一共可取6个点,之前是第一行的所有点加Top2,现在是第一行的某三个点加S1和S2再加Top1了,毕竟Sr被替代以后多占了一个点的位置。于是有了下面的公式。
![]()
与面的公式相比,So并没有变化。之前已经说明S2<=Sr,接下来比较(S1+Top1)与Top2的大小关系就好了。替换后的Top1必然在替换前的Top2之中,却不一定有Top1=first(first是Top2里面的最大值)。替换者S1倘若来自替换前的Top2,则
![]()
否则,
![]()
综合上面两个公式可得,
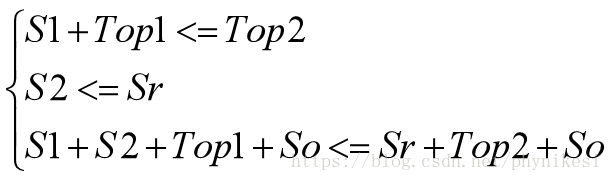
明显地,替换后的代价总和不会比替换前更大,因此,第一行的各个点是不可被取代的。所以调整后的第一行是能保证全节点覆盖的最大路径。
方案二:先找出矩阵中最大的16个点,再从最小的点逐步替换以保证全节点覆盖
1,为避免重复,取半个矩阵元素(矩阵上三角或下三角元素)降序排序。
2, 记前16个元素为Top16,之后的元素为后备队列。
3, 对Top16进行过滤,若某个元素包含的两个节点均出现在更高排序的元素中,则舍弃此元素。如第10位元素包含(3,7),第5位元素包含(2,7),第3位元素包含(3,1),则将第10位元素置为无效值。过滤后进入第4步。
4,若过滤后元素不足16个,则从后备队列依次输出最大值,补足16位进入第3步;若过滤后元素足够16位,进入第5步。
5, 计算Top16尚未覆盖的节点,依次从后备队列输出最大值,对Top16自下而上做假设替换。
6, 若替换某元素后覆盖的节点总数增加,则替换,被替换的元素置为无效值,进入第7步;若对全部16个元素均无法替换,则将后备队列输出值置为无效值。
7, 替换后对Top16重新排序,检测是否覆盖所有节点,覆盖完全则停止,否则进入第5步。





 本文探讨了在给定城市网络容量和距离的情况下,如何通过路径选择最大化网络通信价值。提出了两种策略,一是先覆盖所有节点再优化通信价值,二是先选最大通信价值路径再确保节点全覆盖。
本文探讨了在给定城市网络容量和距离的情况下,如何通过路径选择最大化网络通信价值。提出了两种策略,一是先覆盖所有节点再优化通信价值,二是先选最大通信价值路径再确保节点全覆盖。
















 2299
2299

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








