快速排序算法

概念及其介绍：

快速排序算法是在分治算法基础上设计出来的一种排序算法，和其它排序算法相比，快速排序算法具有效率高、耗费资源少、容易实现等优点

算法思想：

• 先选择一个数作为中间元素par（一般选择最右边的元素），此时，设置两个指针，一个指针（后面讲解为左指针）从前向后遍历，直到遍历到一个大于par的元素，而另一个指针（后面讲解为右指针）从倒数第二个元素开始向前遍历，直到找到一个小于par的元素，然后将这个两个元素进行交换，当左指针大于或者等于右指针时，则遍历结束，将par的值与左指针所指的位置的元素进行交换，这样的话par左边的元素都是小于par的，而右边的元素都是大于par的，这样就左右又分成了 两个子数组
• 利用函数递归，重复上一步操作

（这里以升序为例）

算法演示：

1) 建立 2 个指针（命名为 lo 和 hi），分别指向序列中第一个元素和倒数第 2 个元素，如下图所示：
 

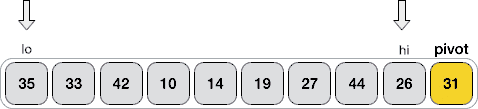
2) lo 指针向右移动，当指向的元素不小于 31 时暂停。显然，当前指向的 35 > 31，所以 lo 暂时不移动；
 

3) hi 指针向左移动，当指向的元素不大于 31 时暂停。显然，当前指向的 26< 31，所以 hi 暂时不移动；
 

4) 交换 lo 和 hi 所指元素的位置，如下图所示：
 

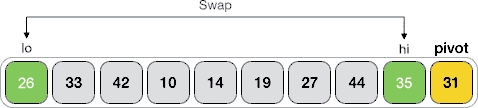
5) 重复执行 2~4 步，直至 lo ≥ hi。此时，将 pivot 元素与 lo 所指元素交换位置。下面的动画演示了整个分割的过程：

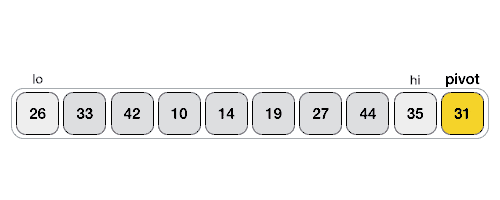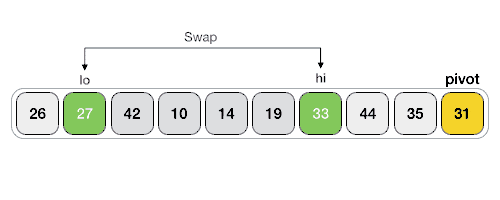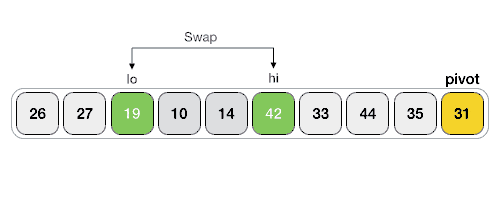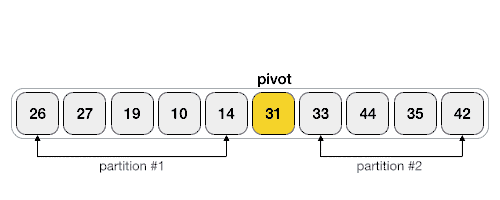
可以看到，最终元素 31 左侧的元素都比它小，右侧的元素都比它大。

算法代码示例：

//分割数组成为相应的子数组
int partition(int arr[], int p, int q)
{
	int temp;//设置一个中间变量用于进行交换
	int lo = p;//设置左指针指向第一个元素的下标
	int ho = q - 1;//设置右指针指向倒数第二个元素的下标
	int centure = arr[q];//作为中间值（一般为最后一个元素）
	while (1)
	{
		//lo向后遍历，直到遍历到一个大于centure的值
		while (arr[lo] < centure)
		{
			lo++;
		}
		//ho向后遍历，直到遍历到一个小于centure的值
		while (arr[ho] > centure && ho > 0)
		{
			ho--;
		}
		//当遍历超出范围之后就跳出循环
		if (lo >= ho)
		{
			break;
		}
		//不然的话就进行交换值
		else
		{
			//交换arr[lo]和arr[ho]
			temp = arr[lo];
			arr[lo] = arr[ho];
			arr[ho] = temp;
			//让lo和ho向前移动一位，继续遍历
			lo++;
			ho--;
		}
	}
	//当遍历完成后，将设置为中间的值交换到中间
	temp = arr[lo];
	arr[lo] = centure;
	arr[q] = temp;
	//返回中间值所在的下标
	return lo;
}
void the_quick_sort(int arr[],int p,int q)
{
	int par;//设置中间元素
	//如果说q - p<= 0的话，说明待排列元素不存在或者说只存在1个元素值，故不需要再进行分割排序
	if (q - p <= 0)
	{
		return;
	}
	else
	{
		//调用partition函数进行分割序列
		par = partition(arr, p, q);//返回中间元素的下标
        //利用函数的递归来完成后面子数组的快速排序
		the_quick_sort(arr, p, par - 1);//中间元素左边的元素都是小于par
		the_quick_sort(arr, par + 1, q);//中间元素右边的元素都是大于par
	}
}