DoG 、Laplacian、图像金字塔详解及MATLAB代码

DoG 、Laplacian、图像金字塔详解

本文前半部分转自博客：http://blog.youkuaiyun.com/yangtrees/article/details/8309594

后半部分的MATLAB代码是自己亲自用过的，分别是二维、三维图像的Gaussian/Laplacian Py r amid MATLAB Code

DoG(Difference of Gaussian)

DoG (Difference of Gaussian)是灰度图像增强和角点检测的方法，其做法较简单，证明较复杂，具体讲解如下:

Difference of Gaussian(DOG)是高斯函数的差分。我们已经知道可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果，即去噪过程，这里的Gaussian和高斯低通滤波器的高斯一样，是一个函数，即为正态分布函数。

那么difference of Gaussian 即高斯函数差分是两幅高斯图像的差，

一维表示：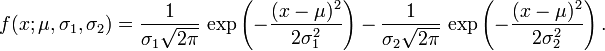

二维表示：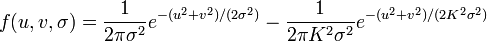

具体到图像处理来讲，就是将两幅图像在不同参数下的高斯滤波结果相减，得到DoG图。

[cpp]  view plain copy print ?

1. GaussianBlur(img,img_G0,Size(3,3),0);  
2. GaussianBlur(img_G0,img_G1,Size(3,3),0);  
3. Mat img_DoG = img_G0 - img_G1;  
4. normalize(img_DoG,img_DoG,255,0,CV_MINMAX);  

 

 

Laplacian图像

计算图像的拉普拉斯是通过Sobel¶操作计算图像在x和y方向的二阶偏导数的和：

voidLaplacian(InputArray src, OutputArray dst, int ddepth, int ksize=1, double scale=1, double delta=0, int borderType=BORDER_DEFAULT)¶

 

当ksize>1使用上述偏导公式计算. 当ksize==1 , 拉普拉斯图像通过如下 aperture计算:

 

[cpp]  view plain copy print ?

1. Laplacian(img,img_Lp,8,1);  

ksize=1,不太明显，选择ksize>1时，比较显著。

 

 

图像金子塔

拉普拉斯金字塔与高斯金字塔是一个图像集合，集合中的所有图像都源于一幅图像，是通过连续下采样获得。

高斯金字塔是向下采样图像，而拉普拉斯金字塔是向上重建图像。

高斯金字塔

Down：降采样（OpenCV里描述成Down，注意也可以说是向上层操作）

从第i层G(i)生成第i+1层G(i+1)：首先使用高斯核进行卷积，然后删除所有偶数行和偶数列，这样获得图像大小仅为上一层的1/4，然后不断迭代。

[cpp]  view plain copy print ?

1. pyrDown(img,img_Down,Size());  

 

Up：（注意不是简单的降采样的逆操作）

从第i+1层G(i+1)生成第i层G(i)：首先每一维都扩大两倍，新的行（偶数行）以0填充，然后使用指定的录波器进行卷积（实际上是在每一维都扩大两倍的滤波器：此滤波器的所有元素都被规范化为4，而不是1。因为在之前所有插入行的像素值都为0，所以这样做是合理的）去估计“丢失”的近似值，这样获得图像大小为上一层的4倍。

[cpp]  view plain copy print ?

1. pyrUp(img_Down,img_Up,Size());  

 

 Laplacian金字塔

高斯金字塔丢失的数据形成了拉普拉斯金子塔，数学公式如下：

L(i)=G(i) - UP(G(i+1))*G(5x5)

OpenCV可以使用：

L(i)=G(i) - PyrUp(G(i+1))

 

[cpp]  view plain copy print ?

1. Mat lp_UpDown = img-img_Up;  

 

Gaussian/Laplacian MATLAB 代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Gaussian/Laplacian Pyramid MATLAB Code for 2D Image %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear
clc

f = imread('orchid.tif');
f = rgb2gray(f);
f = im2double(f);
a = 0.4;
h = [1/4-a/2 1/4 a 1/4 1/4-a/2];

% Build a Gaussian pyramid
N = 3;
g = cell(N,1);
g{1} = f;

for n = 2 : N
  t = imfilter(g{n-1}, h, 'conv', 'same', 'replicate');
  t = imfilter(t, h', 'conv', 'same', 'replicate');
  g{n} = t(1:2:end, 1:2:end); % 下采样
end 

% Build the Lapacian pyramid
L = cell(N,1);
L{N} = g{N};
for n = 1 : N-1
   t = zeros(2*size(g{n+1}));
   t(1:2:end, 1:2:end) = g{n+1};
   t(2:2:end, 2:2:end) = g{n+1};
   t(1:2:end, 2:2:end) = g{n+1};
   t(2:2:end, 1:2:end) = g{n+1};
   f = imfilter(t, h, 'conv', 'same', 'replicate');
   f = imfilter(f, h', 'conv', 'same', 'replicate');   
   L{n} = g{n} - f;
end

for n = 1 : N
    figure(n);
    imshow(L{n});
end

for n = 1 : N
    figure(n+N);
    imshow(g{n});
end
%disp('press any key to continue ...');
%pause;

% Reconstruction using Laplasain Pyramid
im = g{N};
for n = N-1 : -1 : 1
   t = zeros(2*size(im));
   t(1:2:end, 1:2:end) = g{n+1};
   t(2:2:end, 2:2:end) = g{n+1};
   t(1:2:end, 2:2:end) = g{n+1};
   t(2:2:end, 1:2:end) = g{n+1};
   f = imfilter(t, h, 'conv', 'same', 'replicate');
   f = imfilter(f, h', 'conv', 'same', 'replicate');
   im = L{n} + f;
end

figure(N+N+1);
imshow(im);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Gaussian/Laplacian Pyramid MATLAB Code for 3D Image %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear
clc

f = imread('orchid.tif');
%f = rgb2gray(f);
f = im2double(f);
a = 0.4;
h = [1/4-a/2 1/4 a 1/4 1/4-a/2];

% Build a Gaussian pyramid
N = 3;
g = cell(N,1);
g{1} = f;

t=g{1};
for n = 2 : N
  t = imfilter(g{n-1}, h, 'conv', 'same', 'replicate');
  t = imfilter(t, h', 'conv', 'same', 'replicate');
  for i=1:3
    g{n}(:,:,i) = t(1:2:end, 1:2:end,i); % 下采样
  end
end 

% Build the Lapacian pyramid
L = cell(N,1);
L{N} = g{N};

for n = 1 : N-1
   [x,y,z]=size(g{n+1});
   t = zeros(2*x,2*y,z);
   for i=1:z
       t(1:2:end, 1:2:end,i) = g{n+1}(:,:,i);
       t(2:2:end, 2:2:end,i) = g{n+1}(:,:,i);
       t(1:2:end, 2:2:end,i) = g{n+1}(:,:,i);
       t(2:2:end, 1:2:end,i) = g{n+1}(:,:,i);
   end
   f = imfilter(t, h, 'conv', 'same', 'replicate');
   f = imfilter(f, h', 'conv', 'same', 'replicate');   
   L{n} = g{n} - f;
end

for n = 1 : N
    figure(n);
    imshow(L{n});
end

for n = 1 : N
    figure(n+N);
    imshow(g{n});
end
%disp('press any key to continue ...');
%pause;


% Reconstruction using Laplasain Pyramid
im = g{N};
for n = N-1 : -1 : 1
   [x,y,z]=size(im);
   t = zeros(2*x,2*y,z);
   for i=1:z
       t(1:2:end, 1:2:end,i) = g{n+1}(:,:,i);
       t(2:2:end, 2:2:end,i) = g{n+1}(:,:,i);
       t(1:2:end, 2:2:end,i) = g{n+1}(:,:,i);
       t(2:2:end, 1:2:end,i) = g{n+1}(:,:,i);
   end
   f = imfilter(t, h, 'conv', 'same', 'replicate');
   f = imfilter(f, h', 'conv', 'same', 'replicate');
   im = L{n} + f;
end

figure(1+N+N);
imshow(im);