『机器学习』 —— 支持向量机（SVM）上

文章首发地址见个人博客

#支持向量机（Support Vector Machine, SVM）

###1、算法的基本思想
在机器学习算法中，分类问题最基本的想法就是基于训练集D在样本空间中找到一个划分超平面，将不同类的样本分开，但是这样的超平面很多，如何选择“合适的”超平面是我们应当需要考虑的。

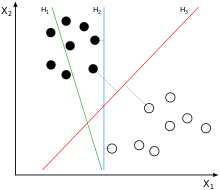
如上图的二维空间中划出的三条超平面($H_1，H_2，H_3$)，显然将$H_3$作为分类的超平面最为合适，其具有较强的鲁棒性和泛化能力。可是这样划分的理论依据又是什么呢？
###2、支持向量机的理论依据
在样本空间中，我们可以以如下的线性方程来描述一个超平面$(w,b)$：
$$w^{T}x+b=0（2.1）$$
其中$w$为超平面的法向量（即与超平面垂直的向量），其决定了超平面的方向，$b$为位移量，决定了超平面与原点之间的距离，样本空间中任意一点$x$到超平面$(w,b)$的距离为：
$$r=\frac{|w^T+b|}{||w||}(2.2)$$
$(figure2.1)$
设：
$$\{\begin{array}{ll}{y}_i=+1,& \text{对于所有的蓝点}\\ y_i=-1,& \text{对于所有的红点}\end{array}(2.3)$$
则有
$$\{\begin{array}{ll}{w}^{T}x+b>0,& \text{yi=+1}\\ w^{T}x+b<0,& \text{yi=−1}\end{array}(2.4)$$
如果我们要求再高一点，假设决策面正好处于间隔区域的中轴线上（如图中所示黑色实线），并且相应的支持向量对应的样本点到决策面的距离为$d$，那么公式$(2.4)$就可以进一步写成：
$$\{\begin{array}{ll}\frac{w^{T}x+b}{||w||}\ge d,& \text{yi=+1}\\ \frac{w^{T}x+b}{||w||}\le -d,& \text{yi=−1}\end{array}(2.5)$$
将$(2.5)$式中左右两边同时除以$d$，并令$\frac{w^T}{||w||d}={w_s}^T$，$\frac{b}{d}=s$，则可得：
$$\{\begin{array}{ll}{w_s}^{T}x+s\ge +1,& \text{yi=+1}\\ {w_s}^{T}x+s\le -1,& \text{yi=−1}\end{array}(2.6)$$
其实，${w_s}^T+s=0$与$w^{T}x+b=0$为同一直线（或超平面），则式$(2.6)$又可写成
$$\{\begin{array}{ll}{w}^{T}x+b\ge +1,& \text{yi=+1}\\ w^{T}x+b\le -1,& \text{yi=−1}\end{array}(2.7)$$

如图$figure2.1$所示，离超平面最近的点称为“支持向量”，两个异类支持向量到超平面的距离之和为：
$$d=\frac{w^T{x}_i+b}{||w||}+\frac{w^T{x}_t+b}{||w||}(2.8)$$
其中$x_i$和$x_t$为支持向量，他们满足$w^T{x}_i+b=1$和$w^T{x}_t+b=-1$
故：
$$d=\frac{2}{||w||}(2.9)$$
我们知道当$d$取得最大值时，超平面恰好属于两类样本点的正中间，此时能较好的划分两类样本，因此问题转化为求参数$w$和$b$在何时的取值使得$d$的值最大
显然当$\frac{1}{||w||}$在约束条件$y_i(w^T{x}_i+b)\ge 1$的约束条件下取最大值的时候$d$可取最大值，问题也可转化为求
$$求\frac{1}{2}||w|{|}^2在约束条件y_i(w^T{x}_i+b)\ge 1下的最小值$$
这就是支持向量的基本型。
如何解决这一问题，过程涉及高等数学中的拉格朗日乘子法来解决，在此不予详细说明，感兴趣的读者可自行查阅书籍。
###3、在Python中使用SVM进行分类

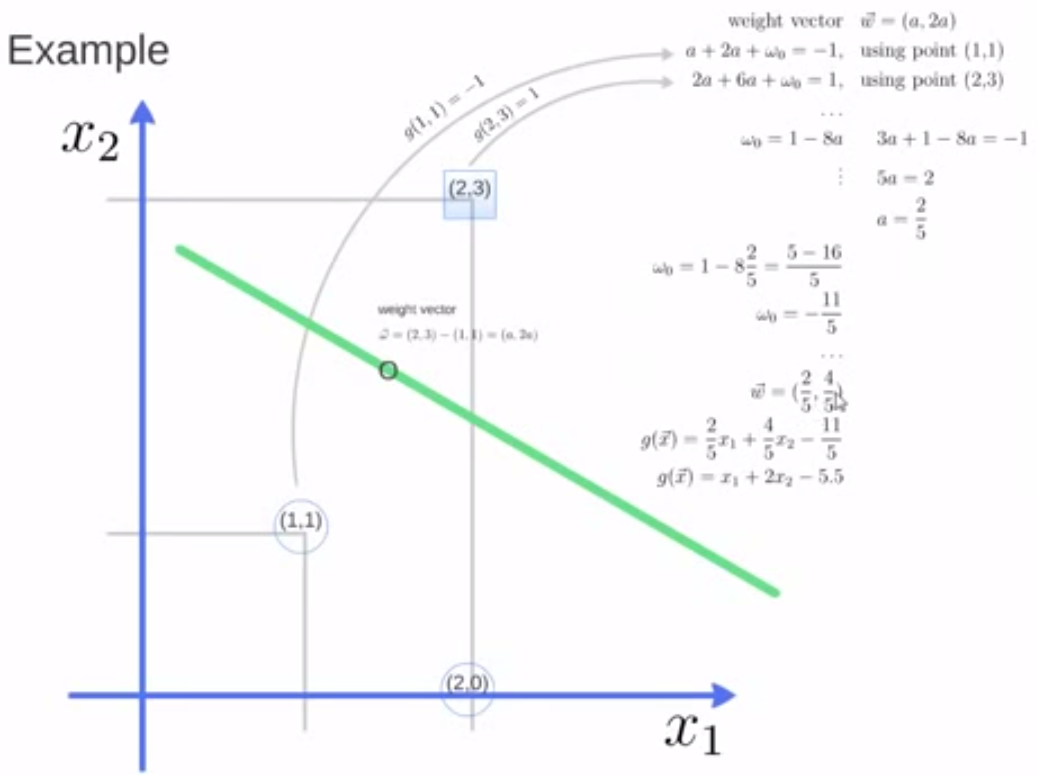
from sklearn import svm
X = [[2, 0], [1, 1], [2,3]]
y = [-1, -1, +1]
clf = svm.SVC(kernel = 'linear')
clf.fit(X, y)  
print clf
# get support vectors
print clf.support_vectors_
# get indices of support vectors
print clf.support_ 
# get number of support vectors for each class
print clf.n_support_ 
a = clf.predict([[3,3]])
print(a)