『机器学习』 —— 最邻近算法（KNN）补充

文章首发地址见个人博客

最邻近算法补充(K-Nearest Neighbor,KNN)

---

1、训练数据集？测试数据集？

我们在使用机器学习算法训练好模型以后，是否直接投入真实环境中使用呢？其实并不是这样的，在训练好模型后我们往往需要对我们所建立的模型做一个评估来判断当前机器学习算法的性能，当我们在真实环境中难以获得真实的标签（Label）这个时候我们往往从原始数据集中划出一部分来作为训练数据集（Train Data Set），而剩下的一部分作为测试数据集（Test Data Set），这样的切分方式称之为 train test split

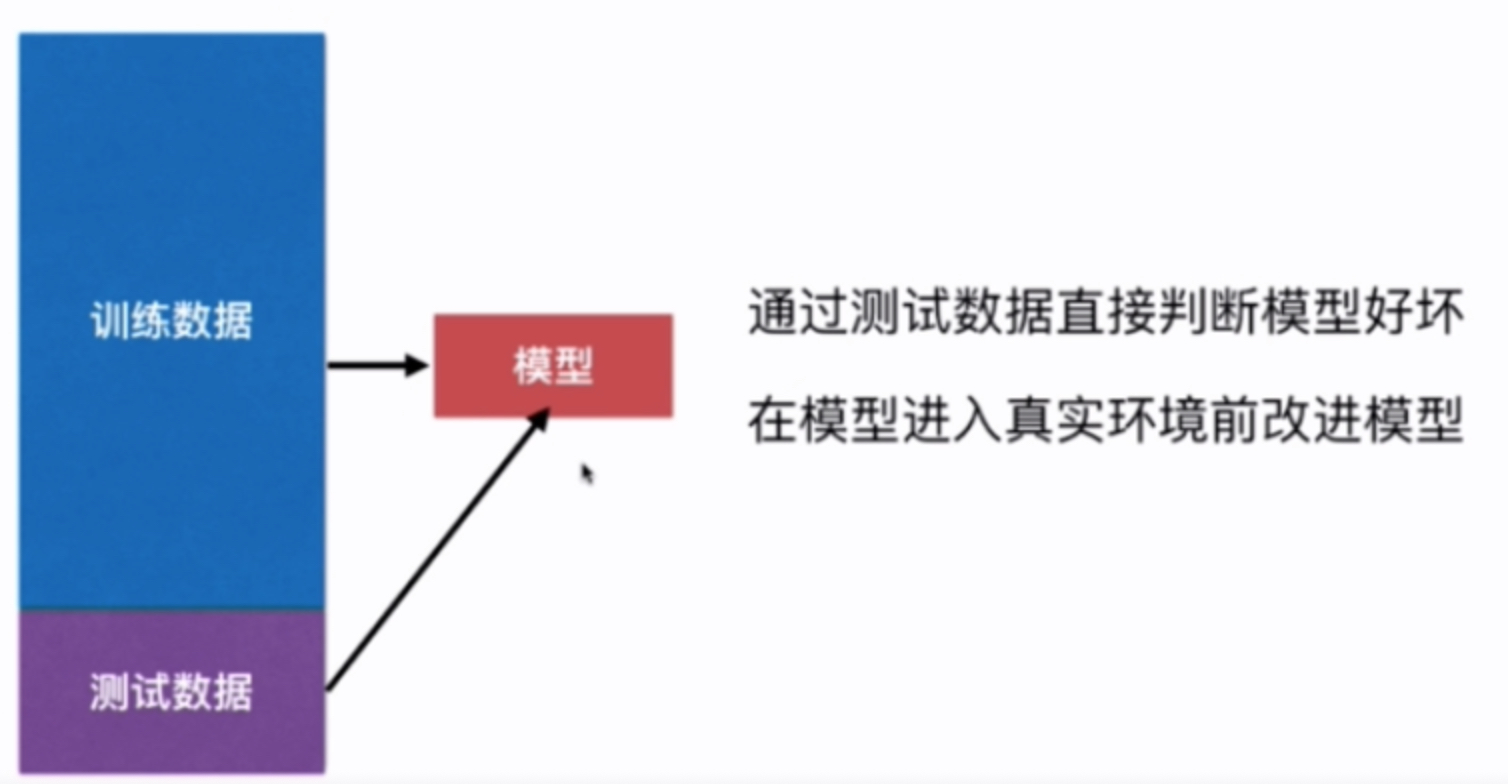
• 以下我们以鸢尾花数据集为例，将原始数据（150个数据样本）拆分为120个训练样本和30个测试样本来测试KNN算法在鸢尾花数据中的准确率

import numpy as np
# sklearn 库中已经封装了train test split 方法 # from sklearn.model_selection import train_test_split from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier

clf = KNeighborsClassifier(n_neighbors=3)

iris = datasets.load_iris()
x = iris.data
y = iris.target

# train test split   
def train_test_split(x, y, test_ratio = 0.2):
    shuffle_indexes = np.random.permutation(len(x))
    test_size = int(len(x) * test_ratio)
    test_indexes = shuffle_indexes[:test_size]
    train_indexes = shuffle_indexes[test_size:]
    x_train = x[train_indexes]
    y_train = y[train_indexes]
    x_test = x[test_indexes]
    y_test = y[test_indexes]
    return x_train, y_train, x_test, y_test

x_train, y_train, x_test, y_test = train_test_split(x, y, test_ratio = 0.2,)

clf.fit(x_train, y_train)
y_predict = clf.predict(x_test)

print("正确率为：", sum(y_predict == y_test)/len(y_test))

运行结果：
————————————————————————————————————————————————————————————
正确率为： 1.0 (每次运行不一样)

• 下面以sklearn中的手写数字数据集为例，演示train test split的使用以及算法准确度的使用方法
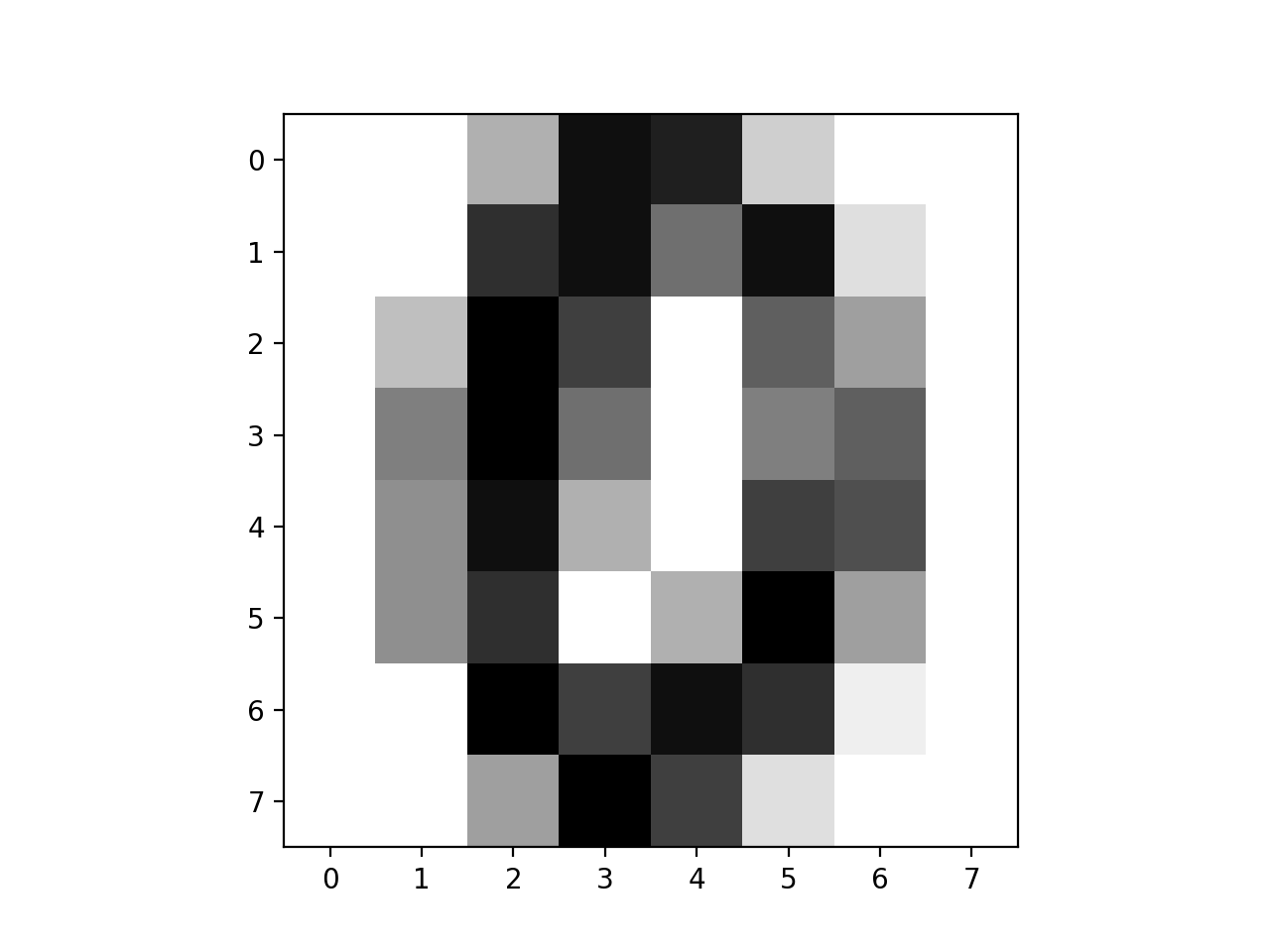
  首先对digit这个数据集做一个简单介绍，在digit这个数据集里面每一个样本对应一个像素为8乘8的图像，每一个像素点为1-16表示的颜色深度，从而用这64个像素点就表示了一幅图像。
  

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
clf = KNeighborsClassifier(n_neighbors=3)

digits = datasets.load_digits()

x = digits.data
y = digits.target

some_digit = x[666]
print(y[666])

# some_digit_image = some_digit.reshape(8, 8) 
# plt.imshow(some_digit_image, cmap = matplotlib.cm.binary) 
# plt.show()   

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

clf.fit(x_train, y_train)
# sklearn自带的计算准确率的方法，出入测试数据的特征向量和标签即可
score = clf.score(x_test, y_test)

print("正确率为:", score)
——————————————————————————————————————————————————————————————
运行结果：
正确率为: 0.9888888888888889

3、超参数和模型参数

• 超参数：在算法运行前需要决定的参数
  • 一个较好的超参数取决于
    • 领域知识
    • 经验数值
    • 实验搜索
• 模型参数：算法过程中学习的参数

KNN算法没有模型参数；
KNN算法中的k是一个典型的超参数。

下面仍以手写数字的数据为例，讲述如何在KNN算法中用实验搜索的方法来确定合适的k值

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

digit = datasets.load_digits()

x = digit.data
y = digit.target

#关于random_state的用法读者可以自行百度
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=666)

best_score = 0.0 
best_k = -1 
for k in range(1, 11):
    clf = KNeighborsClassifier(n_neighbors=k)
    clf.fit(x_train, y_train)
    score = clf.score(x_test, y_test)
    if score > best_score:
        best_k = k
        best_score = score

print("best_k = ", best_k)
print("best_score", best_score)
————————————————————————————————————————————————————————
运行结果：
best_k =  4
best_score 0.9916666666666667

在KNN算法中还存在一个参数weights，默认情况下weights = uniform 而当weights = distance时，KNN算法则会考虑当前样本到邻近K个样本的距离权重

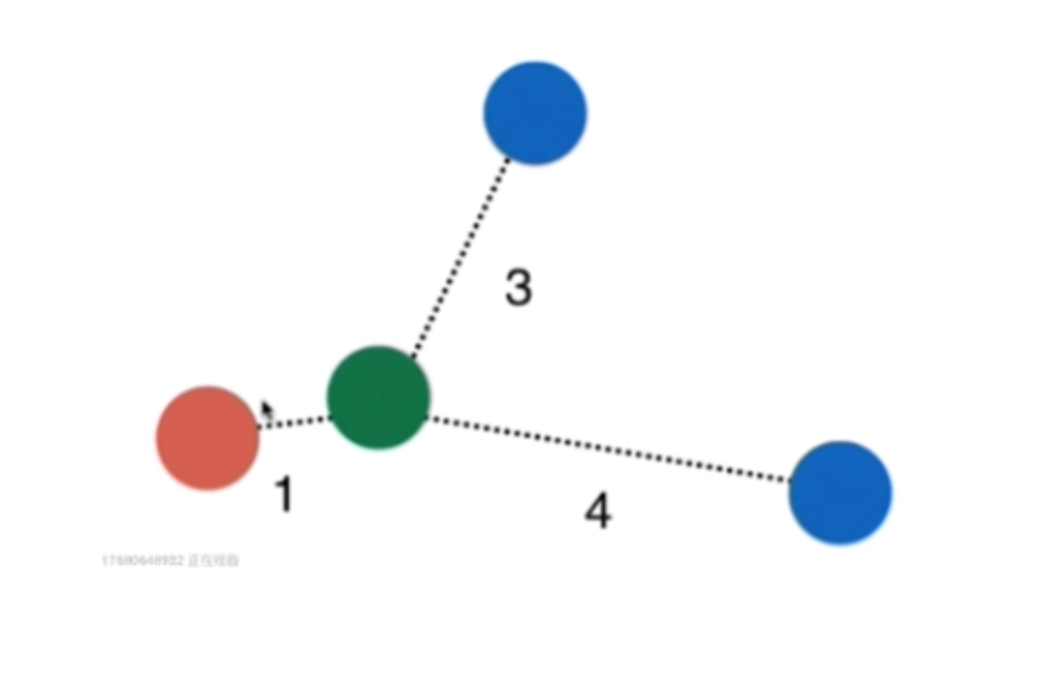
权重我们通常取距离的倒数，则在上图中我们知道:

• 红色的权重：1
• 蓝色的权重：1/3 + 1/4 = 7/12

显然绿色小球应该被标记为红色，因此在KNN算法中weights的取值对于算法运行的结果也是有影响的
考虑距离？不考虑距离
同样我们以digit的数据集以实验搜索的方法来探寻weights的最佳取值

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

digit = datasets.load_digits()

x = digit.data
y = digit.target

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=666)

best_method = "" best_score = 0.0 best_k = -1 for method in ["uniform", "distance"]:
    for k in range(1, 11):
        clf = KNeighborsClassifier(n_neighbors=k, weights=method)
        clf.fit(x_train, y_train)
        score = clf.score(x_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_method = method

print("best_k = ", best_k)
print("best_score", best_score)
print("best_method = ", best_method)
——————————————————————————————————————————————————————
运行结果：
best_k =  4
best_score 0.9916666666666667
best_method =  uniform

4、关于距离

至今我们在KNN算法中计算两个样本点所用的距离定义叫做欧拉距离
$$\sum _{i=1}^n\sqrt{(x_i^{(a)}-x_i^{(b)}{)}^2}=(\sum _{i=1}^n{|x_i^{(a)}-x_i^{(b)}{|}^2)}^{\frac{1}{2}}$$

另一种距离表示方式称之为曼哈顿距离

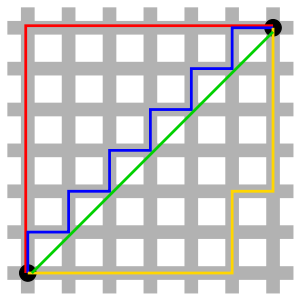
其表示为：
$$\sum _{i=1}^n|{x_i}^{(a)}-{x_i}^{(b)}|=（\sum _{i=1}^n{|{x_i}^{(a)}-{x_i}^{(b)}|}^1{）}^{\frac{1}{1}}$$

仔细对比两个距离公式：

$$（\sum _{i=1}^n{|{x_i}^{(a)}-{x_i}^{(b)}|}^1{）}^{\frac{1}{1}}\to \to \to \to (\sum _{i=1}^n{|x_i^{(a)}-x_i^{(b)}{|}^2)}^{\frac{1}{2}}$$

得到一般式：
$$（\sum _{i=1}^n{|{x_i}^{(a)}-{x_i}^{(b)}|}^p{）}^{\frac{1}{p}}$$

这个距离称之为明可夫斯基距离
从而引出KNN算法的另外一个超参数，这个参数就是这里的p
同样我们使用上述方法来查找最合适的p值，代码如下：

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

digit = datasets.load_digits()

x = digit.data
y = digit.target

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=666)

best_p = -1 best_score = 0.0 best_k = -1 for k in range(1, 11):
    for p in range(1, 6):
        clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p=p)
        clf.fit(x_train, y_train)
        score = clf.score(x_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_p = p

print("best_k = ", best_k)
print("best_score", best_score)
print("best_p = ", best_p)
————————————————————————————————————————————
运行结果：
best_k =  3
best_score 0.9888888888888889
best_p =  2