java浮点数精度问题及解决方案

java开发中浮点运算的精度误差是高频技术难点，其根本原因在于二进制浮点表示与十进制小数之间存在的结构性矛盾。IEEE 754标准定义的存储方式使部分十进制数无法获得精确二进制表达，这种底层机制导致计算结果出现微偏差。以下是系统性分析与解决方案：

一、精度问题的根源

1.二进制表示缺陷

十进制小数（如0.1）在二进制中可能表示为无限循环小数（0.000110011…）。由于float（23位尾数）和double（52位尾数）的存储位数有限，必须对超出部分进行截断处理。这种截断会导致舍入误差，从而引发浮点数运算时的精度问题。
示例：

System.out.println("0.1 + 0.2 = " + (0.1 + 0.2));// 输出0.30000000000000004

运行结果：

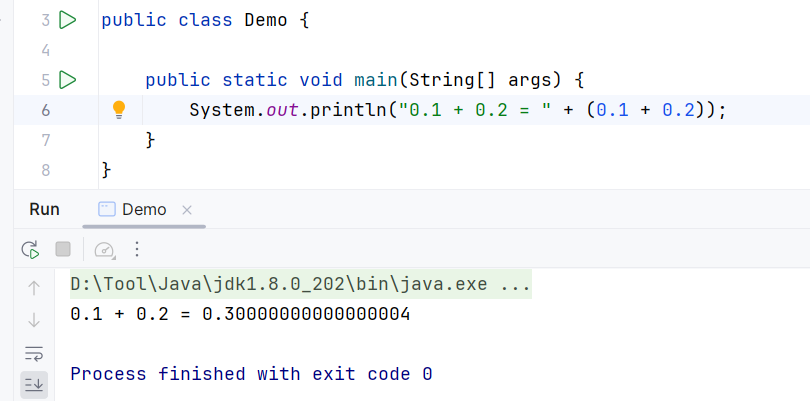
2.大数精度丢失
浮点数在表示极大或极小时，由于指数位有限，无法区分相邻数值，从而在运算过程中产生精度误差，导致计算结果不准确。

float f1 = 2324234234234234f;
float f2 = f1 + 1;
System.out.println(f1 == f2); // 输出true（精度不足导致无法区分）

运行结果：

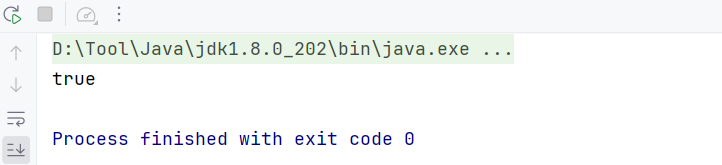
3.运算误差累积
在连续运算过程中，由于二进制表示的固有缺陷，舍入误差会不断累积放大，最终导致计算结果与实际情况出现显著偏差。

double sum = 0;
for (int i = 0; i < 10; i++) 
	sum += 0.1;
System.out.println(sum); // 输出0.9999999999999999

运行结果：

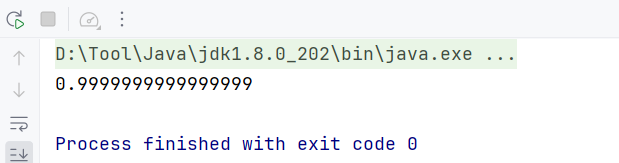
二、解决方案

1. BigDecimal：高精度计算首选

• 正确构造方式：

  • 字符串构造：new BigDecimal("0.1")
  • 静态方法：BigDecimal.valueOf(0.1)
  • 避免double构造：new BigDecimal(0.1) 会继承精度误差。

• 运算与舍入控制：

BigDecimal a = new BigDecimal("0.1");
BigDecimal b = new BigDecimal("0.2");
BigDecimal sum = a.add(b); // 精确得0.3
// 除法需指定舍入模式
BigDecimal quotient = a.divide(b, 2, RoundingMode.HALF_UP); // 0.50

2. 浮点数比较：设定误差范围

避免直接使用==，改用BigDecimal比较：

BigDecimal x = new BigDecimal("1.0").subtract(new BigDecimal("0.9"));
BigDecimal y = new BigDecimal("0.1");
boolean isEqual = x.compareTo(y) == 0; // true

3. 整数运算替代法

将浮点转换为整数（如货币单位“分”代替“元”），计算后再转换：

long cost1 = 1000; // 10.00元
long cost2 = 75;   // 0.75元
long totalCosts = cost1 + cost2 ; // 1075分
System.out.println(totalCosts / 100.0); // 10.75元

适用场景：小数位数固定（如金融计算）。

4. 第三方数学库

如Apache Commons Math提供高精度工具：

double result = Precision.add(0.1, 0.2);

三、总结

1. 精确场景禁用float/double

   在金融计算、计量统计等关键领域，必须使用BigDecimal进行精确计算。

2. 控制输出精度：
   对于非精确计算场景，合理控制精度可有效防止结果异常。

double num = 0.1 + 0.2;
System.out.printf("%.2f", num); // 格式化输出为0.30

结果：

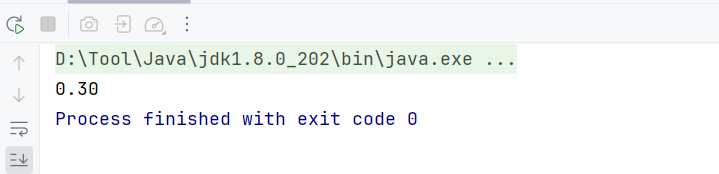
3.避免链式浮点运算：

通过拆分步骤或引入中间变量来减少误差累积。灵活应用BigDecimal、误差范围、整数替代等策略，可显著提升数值计算的准确性。精度问题的本质在于存储和计算之间的权衡——根据实际需求选择合适的工具才是解决问题的关键。