三角形从上走到下问题：120、

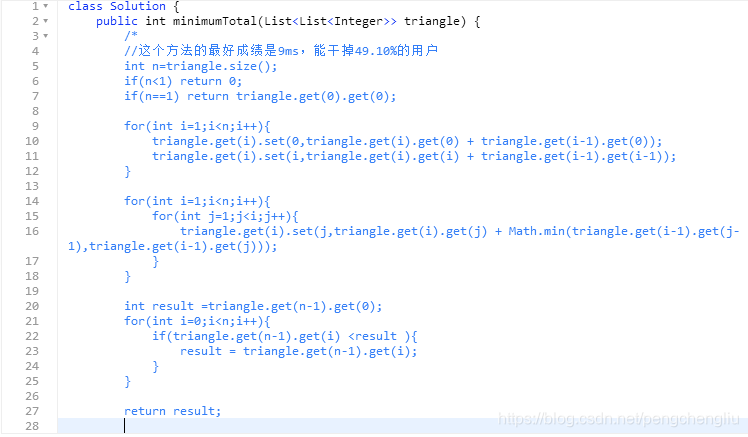
【题目描述】                                                                                                                                        点击此处返回总目录   【首先想到的方法：自上而下】 类似“二维数组从左上角走到右下角”这一类题目的思想。 首先，对于两条边的值等于上面的值加上自己的值。           dp[i][0] = dp[i-1][0]+a[i][j]       dp[i][n] = dp[i-1][n-1]+a[i][n] 然后，中间的值为min(左上角，右上角)+本身。           dp[i][j] = Math.min(dp[i-1][j-1] ,dp[i-1][j]) + a[i][j]   算法如下：   分析：这个算法空间复杂度为0。直接使用了原来的List存放结果。但是时间较慢，最好成绩9ms,只能干掉49%的用户。   【改进1：自下而上】 采用自下而上的方法。这样就不用单独处理两边的数了。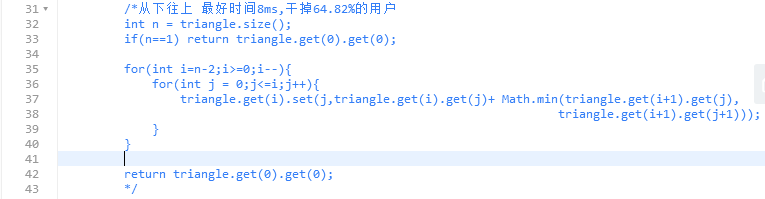 dp[i][j] = min(dp[i+1][j],dp[i+1][j+1]) +dp[i][j]   代码：   分析： 代码量减少了很多。速度提高了一点。空间复杂度为0. get()，set()操作太多，可能限制了速度。不如单独用一个二维数组来存放结果。   【改进2：用二维数组单独存放结果】   分析：减少了get(),set()操作之后，速度又有很大提高，可以干掉94.59%的用户了。说明时间已经可以了。 但是呢，空间复杂度是O(n*n)，不是最好的。 发现dp[n][n]这个数组，首先存放最后一行，然后存放倒数第二行，再算倒数第三行。。。算第n行的时候，只用到第n+1行的数。所以干脆就搞一行得了。用这行的数计算的数还保存到这一行里面。而且不冲突。 dp[j] = Math.min(dp[j],dp[j+1]) + a[i][j]   另外，58行这个地方，每次都get(i).get(j)，其实get(i)可以先提前算好。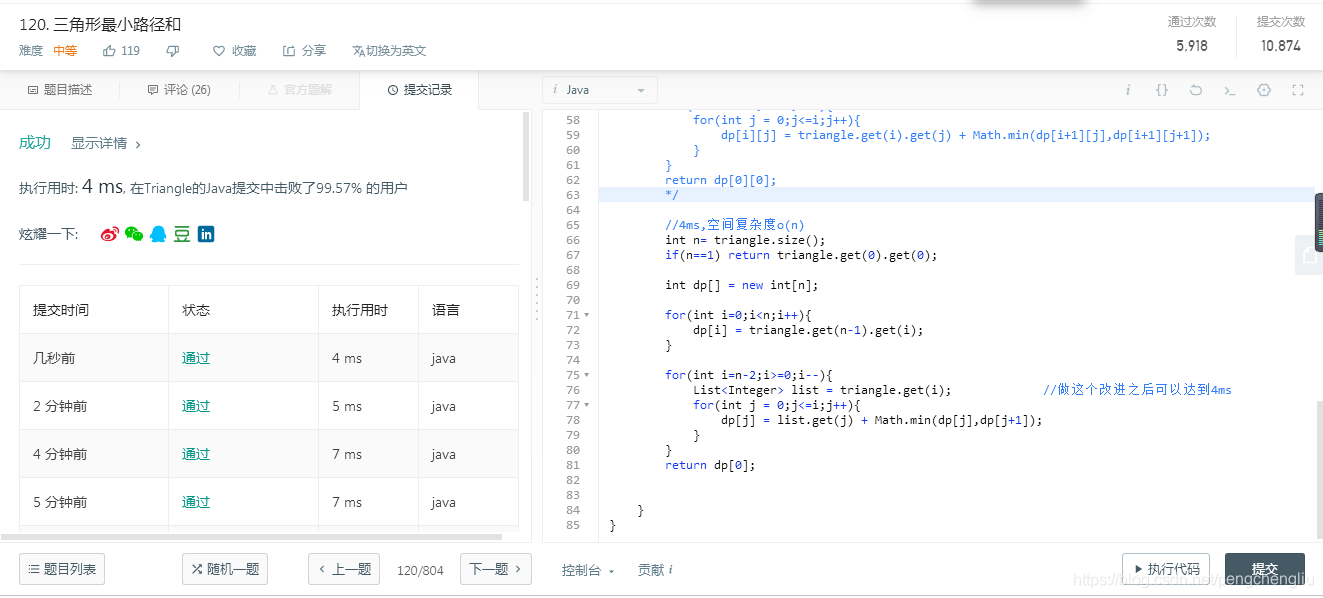   【改进3：O(n)空间复杂度】 代码：   最终结果，o(n)空间复杂度。时间4ms，可以干掉99.57%的用户。是很满意的结果。     【运行结果】