121、123、122 买机票的最佳时机

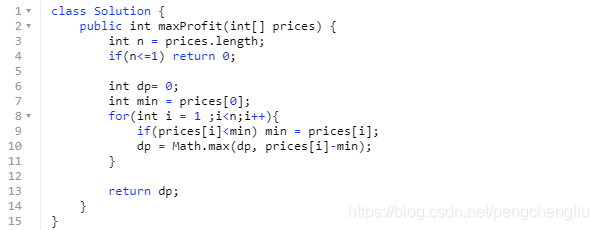
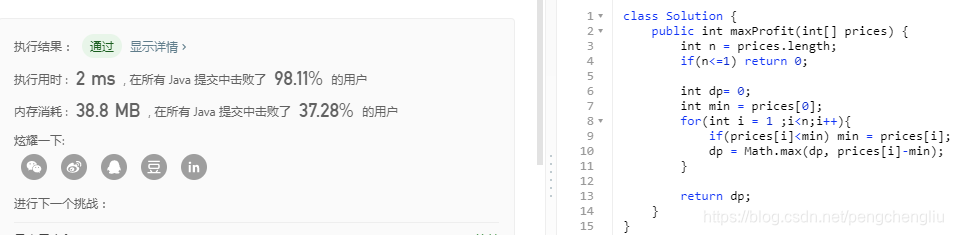
121  只能进行一次交易，求最大收益                                                                                            点击此处返回总目录 123  可以进行2次交易，手上最多只能持有一只股票，求最大收益 122  可以进行任意次交易，手上最多只能持有一只股票，求最大收益       一、121 只能进行一次交易，求最大收益 【题目】     【分析】 只能交易一次。 前i天的最大收益 = max{前i-1天的最大收益，第i天的价格-前i-1天中的最小价格}   【代码】   【结果】     ---------------------------------------------------------------------------------------------------------------------------------------- 二、123  可以进行2次交易，手上最多只能持有一只股票，求最大收益   【题目】   【分析】 可以进行2次交易，即：买-卖-买-卖。 第一题中，我们已经知道了给定连续的n天，一次交易能去得到的最大收益。 我们可以借助第一题来做这一个题：遍历每一个点，作为分割点。对于每一个分割点i，求出从第0天到第i天的最大收益，和从第i天到第n-1天的最大收益，然后相加即为以第i天为分界的最大收益。 因此： for(int i = 0; i< n; i++){     最大收益=max{最大收益，从第0天到第i天交易一次的最大收益 + 从第i天到第n-1天的最大收益}; }   代码如下： 结果：   结果惨不忍睹啊。。。   为什么结果这么差呢？因为计算了很多遍重复的。比如： 当i = 5为分界线的时候： 为了计算前5天的最大收益：计算了前1天的最大收益，前2天的最大收益，前3天的最大收益，前4天的最大收益，前5天的最大收益。 为了计算从第i天到第n-1天的最大收益：计算了从第5天到第6天的最大收益，从第5天到第7天的最大收益...   当i=6为分界线的时候： 为了计算前6天的最大收益：计算了前1天的最大收益，前2天的最大收益，前3天的最大收益.... 为了计算从第i天到第n-1天的最大收益：计算了从第5天到第6天的最大收益，从第5天到第7天的最大收益...   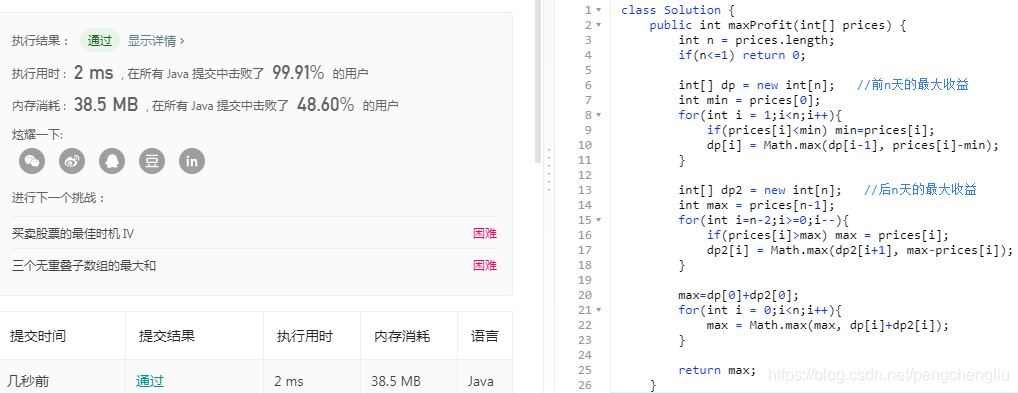重复太多了。改进如下： 1. 前n天的最大收益求一遍就行了。保存到dp[n]中。 2. 后面的也不需要这么求。只需要从后往前遍历一遍数组，记录下当前遇到的最大值。     后n天的最大收益dp[n] =max {dp[n-1], max-num[i]}   改进后如下： opt = max{opt, dp[i]+dp2[i]} dp[i] = max{dp[i-1], num[i]-min} dp2[i] = max{dp2[i+1], max-num[i]}     【代码】   【结果】   效果不错。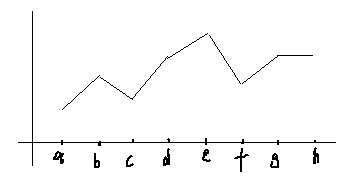     --------------------------------------------------------------------------------------------------------------------------------------- 三、122  可以进行任意次交易，手上最多只能持有一只股票，求最大收益   【题目】     【分析】 比如：   从a到b的最大收益是：ab 从a到c的最大收益是：ab，因为bc下降。 从a到d的最大收益是：ab+cd，即a买b卖、c买d卖。不是ad，因为ad肯定没有ab+cd高。 从a到e的最大收益是：ab+cd+de。 从a到f的最大收益是：ab+cd+de。 从a到g的最大收益是：ab+cd+de+fg。 从a到h的最大收益是：ab+cd+de+fg。（gh=0）   由此，可以得出规律，如果num[i]-num[i-1]>0，则收益就增加num[i]-num[i-1]。   【代码】   【结果】