思路:让递增子序列最长,就要使子序列增加得尽可能慢
用一个dp数组来维护最长递增子序列末尾元素的最小值。即dp[i]表示递增子序列长度为i时,末尾元素的最小值为dp[i]。
比如nums={4,1,8,7,12,5} vector<int>dp(nums.size()+1,0)
int curlen=1,记录目前最长递增子序列的长度,最开始为1
dp[0]没有意义。dp[1]=nums[0].
插入4,dp=[0,4] dp[1]表示此时长度为1的最长递增子序列的末尾元素为4,curlen=1.
插入1,dp=[0,1] 1比4小,用1去覆盖4,从4开始的最长递增子序列的长度必定不大于以1开始的最长递增子序列的长度。比如 1后面如果还有2或者3的话,1可以接收,4则不可以;如果1后面全是比1和4大的话,则以4开头和以1开头,最长递增子序列的长度都相同。所以为了求最长的递增子序列的长度,这里要替换。curlen=1
插入8,dp=[0,1,8] 如果nums[i]比dp的最后一个元素大,直接放进dp中。curlen=2
插入7,dp=[0,1,7]。curlen=2
插入12,dp=[0,1,7,12]。curlen=3。 1 7 12
插入5,dp=[0,1,5,12] 可以插入5,因为dp数组并不代表的是最长递增子序列,只是代表长度为i的最长递增子序列的末尾元素的最小值为dp[i]。
比如dp[1]=1,表示长度为1的最长递增子序列的末尾元素的最小值为1。此时最长递增子序列为 1
dp[2]=5,表示长度为2的最长递增子序列的末尾元素的最小值为7。此时最长递增子序列为 1 5
dp[3]=12,表示长度为3的最长递增子序列的末尾元素的最小值为12。此时最长递增子序列为 1 5 12
最长递增子序列的长度是通过curlen来实时更新的。
代码如下:

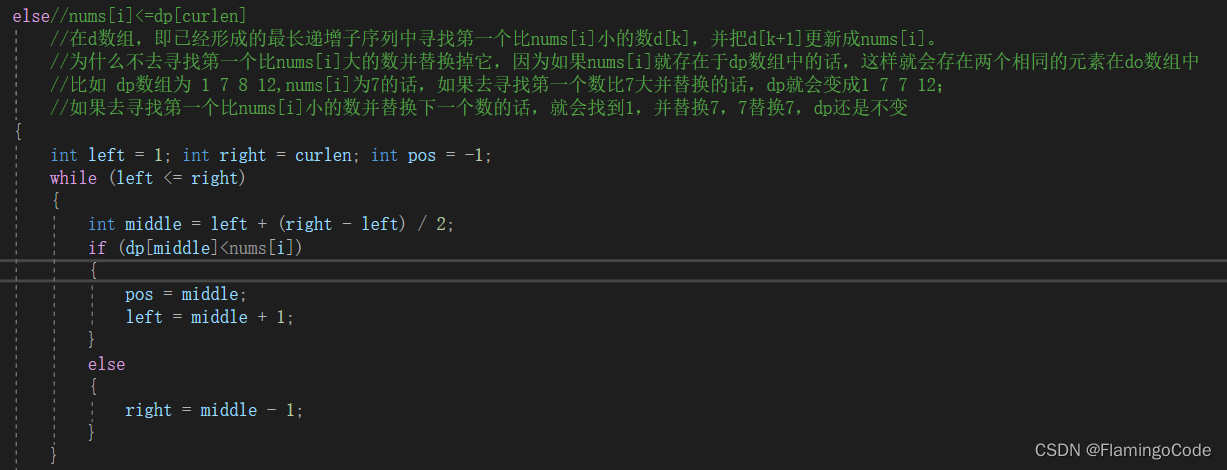
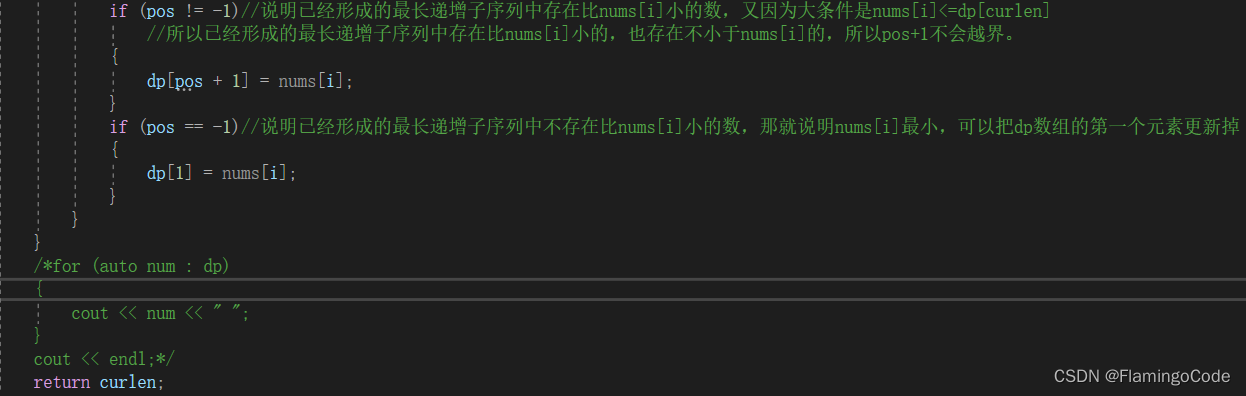




 文章介绍了如何使用动态规划方法解决找到数组中最长递增子序列的问题。通过维护一个dp数组,存储以每个元素结尾的最长递增子序列的最小末尾值,逐步更新最长递增子序列的长度。这种方法的关键在于比较新元素与dp数组中已有的值,以确定何时更新dp数组并更新当前最长递增子序列的长度。
文章介绍了如何使用动态规划方法解决找到数组中最长递增子序列的问题。通过维护一个dp数组,存储以每个元素结尾的最长递增子序列的最小末尾值,逐步更新最长递增子序列的长度。这种方法的关键在于比较新元素与dp数组中已有的值,以确定何时更新dp数组并更新当前最长递增子序列的长度。
















 1465
1465

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








