模式分类（二）贝叶斯决策论

最新推荐文章于 2023-10-25 21:03:11 发布

原创

最新推荐文章于 2023-10-25 21:03:11 发布 · 574 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习

本文深入探讨了贝叶斯决策论在模式分类中的作用，通过实例解释了如何根据先验概率和条件概率进行决策。讨论了连续特征的广义贝叶斯方法，引入损失函数和条件风险的概念，并通过案例分析了如何选择风险最小的决策方案。总结了最小误差率和最小风险的贝叶斯决策策略，以及它们之间的对比。

入门理解：
https://blog.youkuaiyun.com/zjy_snow/article/details/82592718

数学基础：
https://blog.youkuaiyun.com/peachluo/article/details/110289006

贝叶斯决策论

理解

贝叶斯决策就是利用贝叶斯理论进行决策分类。

原理

观察到一系列的特征x=[x1,x2,…,xn]T，那么如何对这一系列的观察值进行分类？即求解概率P(ωi|x)P(ωi|x)，可以理解为在观察到特征x的前提下，观察到的现象属于ωi类的概率是多大。
例子：
以观察细胞特征并判断细胞是否正常的栗子来说明。已知条件：观察到的细胞特征是n维向量x=[x1,x2,…,xn]T细胞分为正常细胞ω1类和异常细胞ω2类，P(ω1)+P(ω2)=1。
如果仅从先验概率P(ω1)和P(ω2)对细胞进行分类，合理的方法是：当P(ω1)>P(ω2)时，认为是正常细胞，反之则是异常细胞；
但实际不可能这么做，因为一般情况下先验概率都是个常量，而且我们对细胞的分类是会随着观察值的改变而改变的，那么如果我们现在观察到了细胞特征xx，在特征x的基础上要判断细胞是属于哪一类，就是要判断P(ω1|x)和P(ω2|x)的大小。
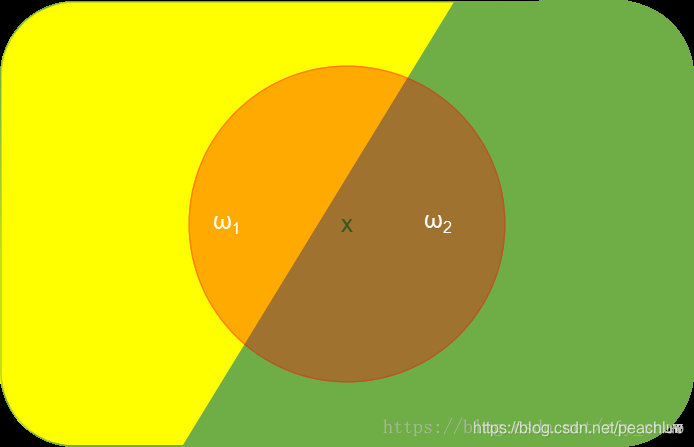
在这里插入图片描述
结合贝叶斯公式，那么就把求解P(ωi|x)转变为了求解先验概率P(ωi)和条件概率P(x|ωi)