数据挖掘|基础|聚类分析

常见的聚类分析方法：

k均值-常见、效率max

聚类的应用：判别新用户的类型

聚类是数据驱动 所以数据很重要 数据的特征的选取：
身高体重 城市 成绩 

聚类过程中也有个反馈环

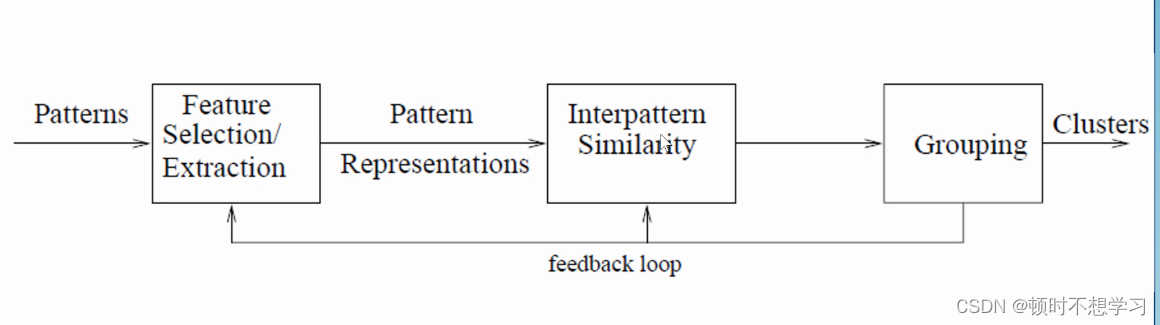
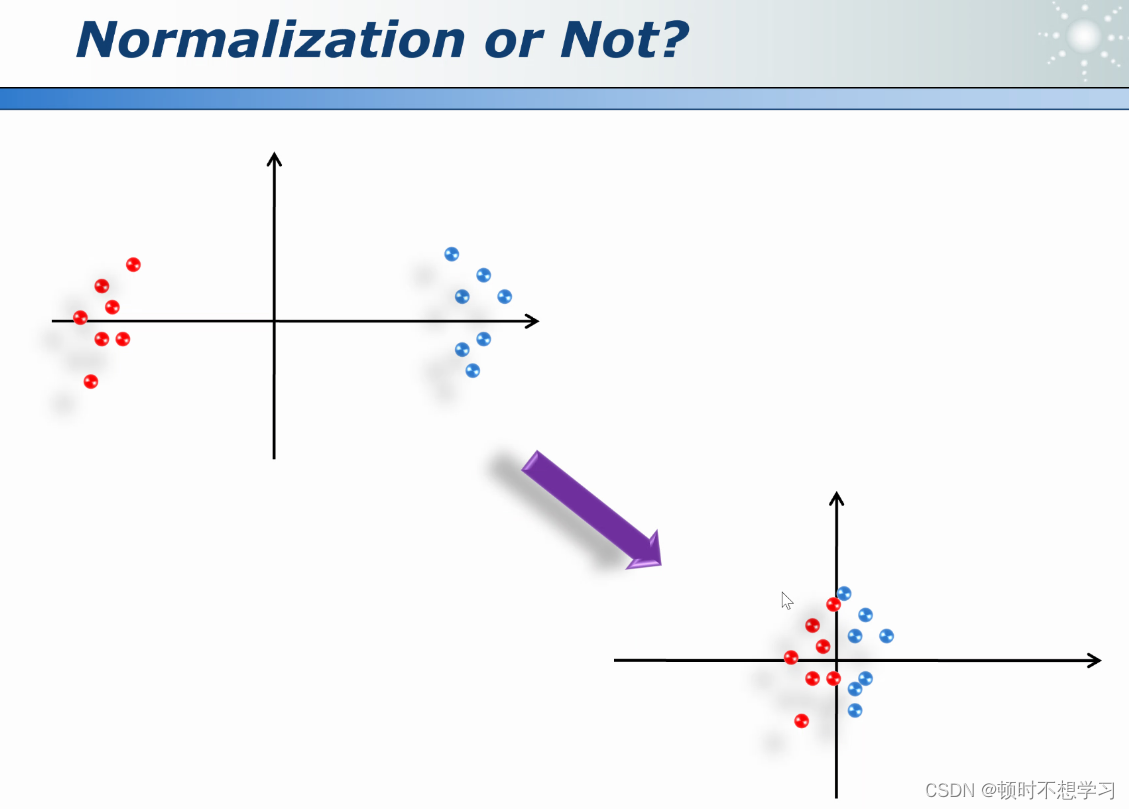
 除了，还需要考虑数据的标准化 缩放的比例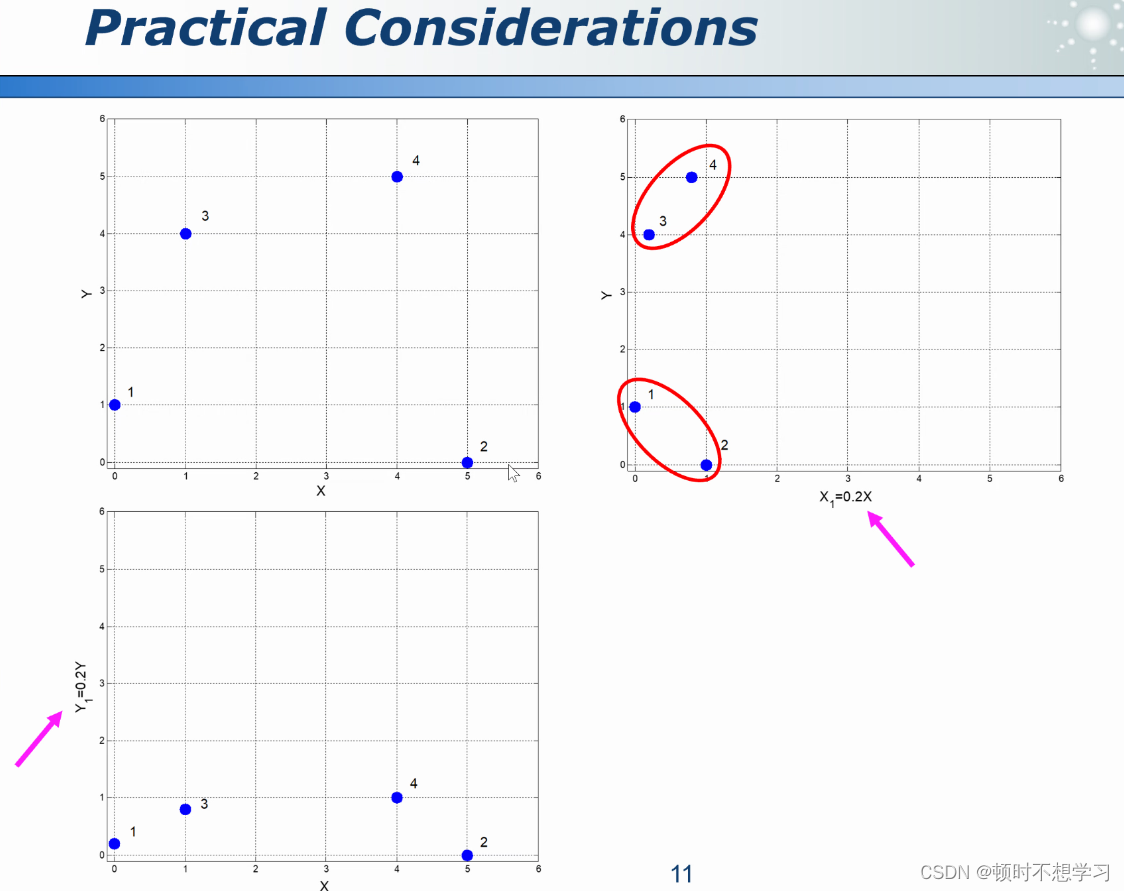

 标准化 也需要考虑

 聚类评估的问题：

目的：簇内的距离尽可能的小，簇间的距离尽可能大

 b（i）表示与其他簇的距离

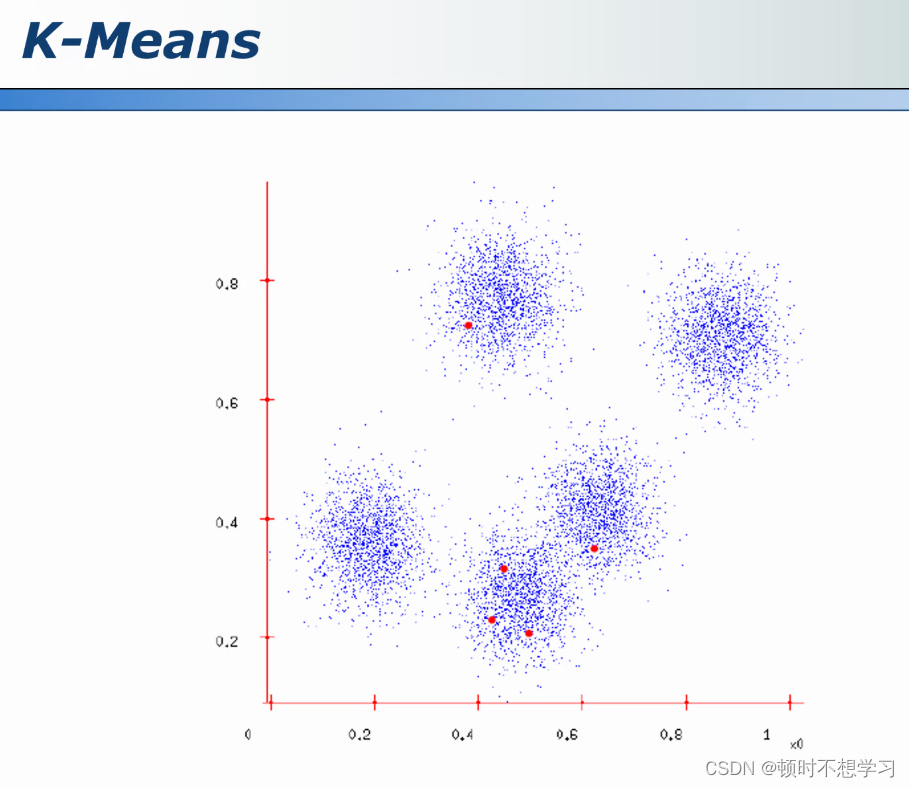
 k均值 

原理：k是人为设定的 先 确定了k之后 ，假设k=5

确定了5个簇  那就把5个点作为中心点  若a点与5点中的一点距离最小 就被划分到那一簇

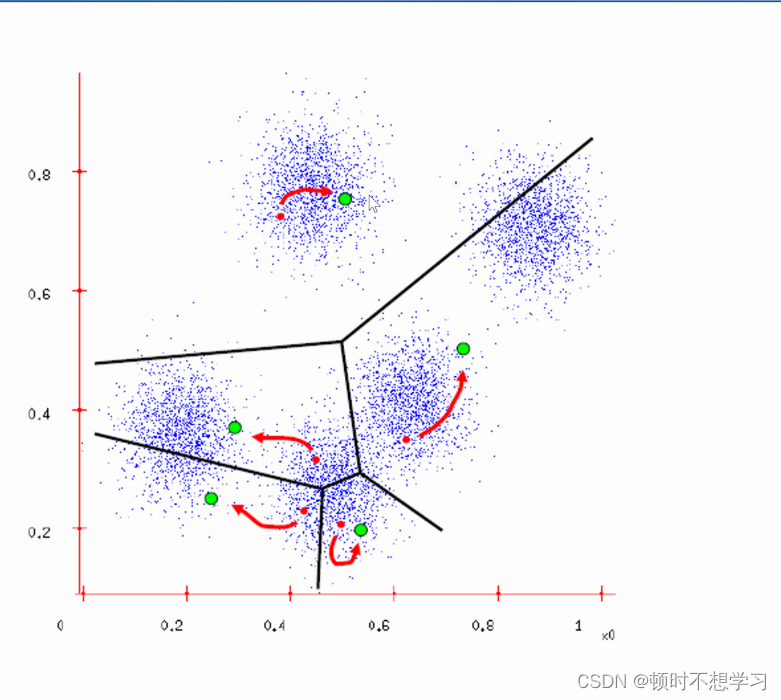
 更换中心点  （图中绿色的那个），再重新划分簇，重新划分中心点 不断迭代

当中心点不再变化 迭代结束

最后分成的界面是连续性的

 

 不适合 不规则聚类形状

对初始点不同的选取 最后的结果也不一样

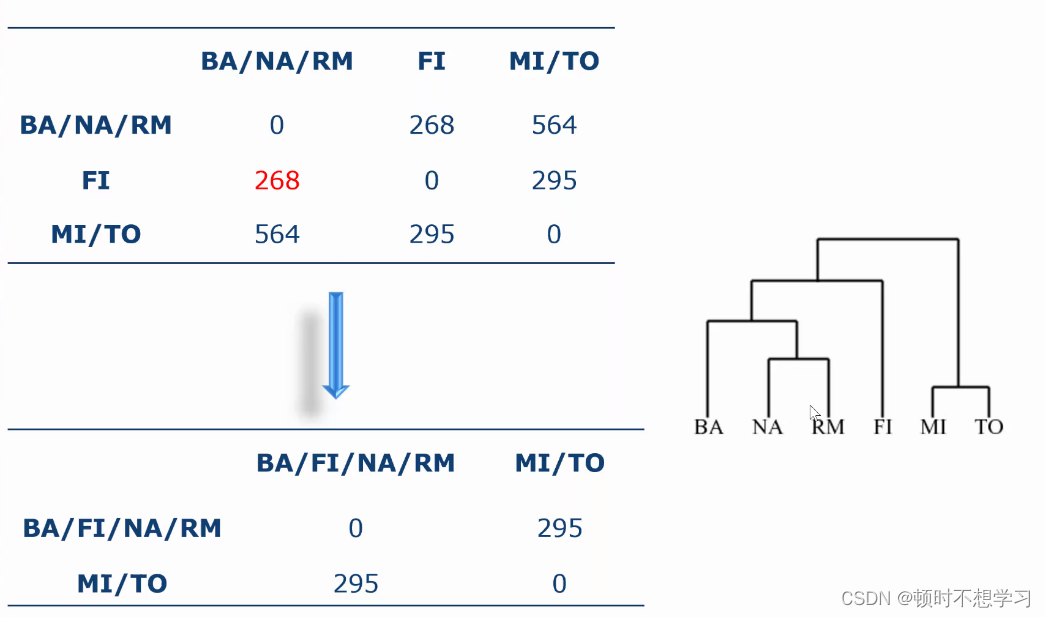
另一个方法：定义距离

 方法3 高斯模型

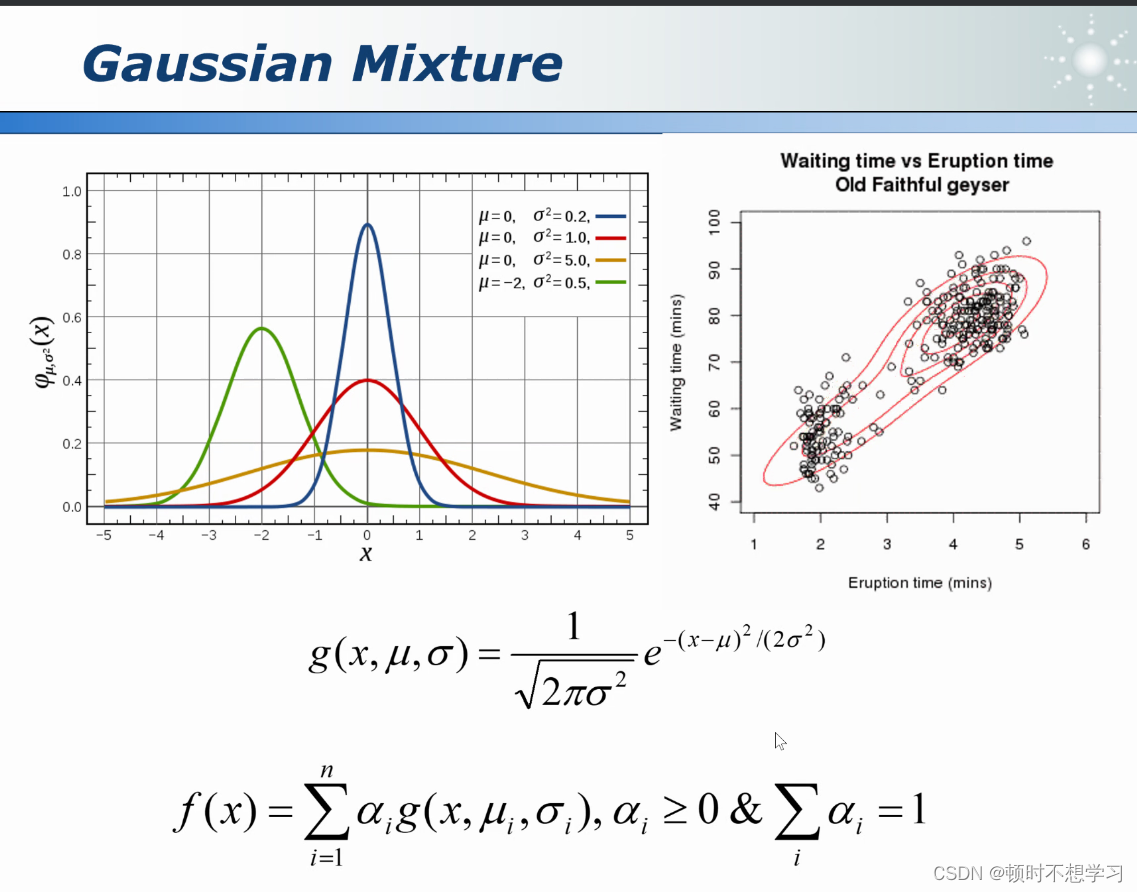
 通过调参 均值 方差都会发生变化 

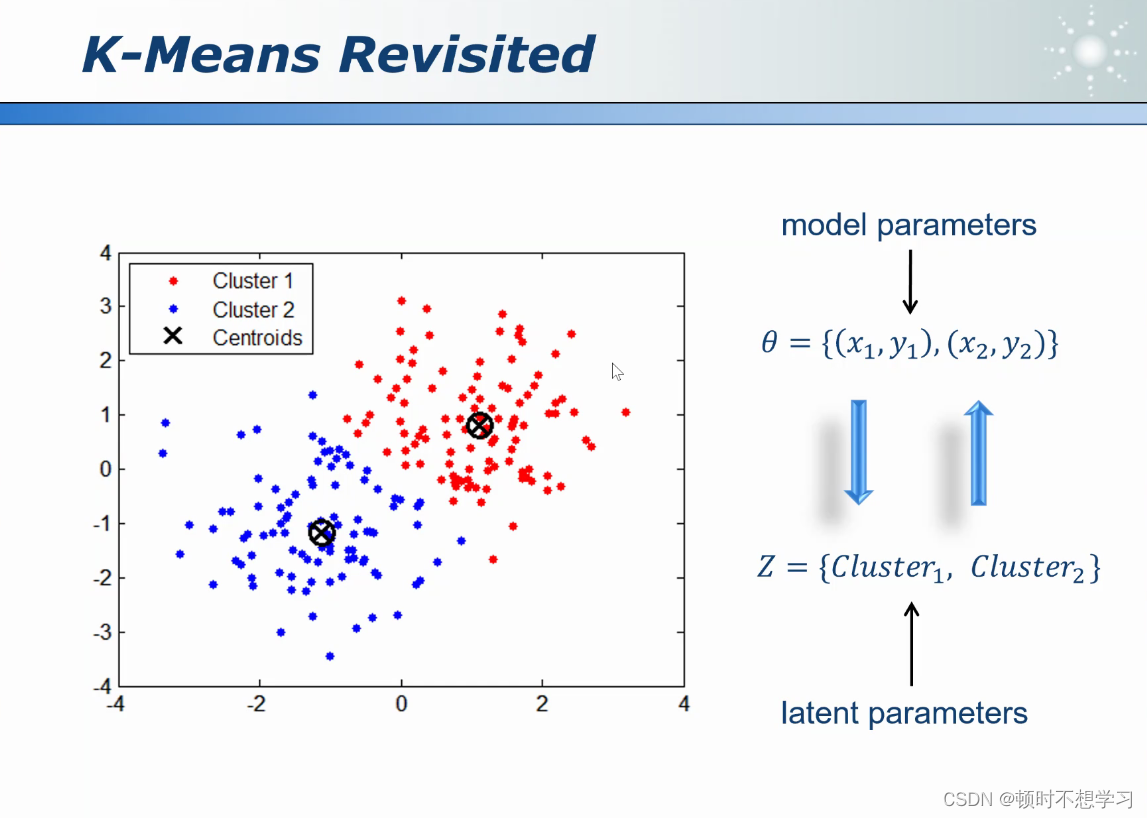
在看k均值 ，确定两个中心点

 eg 硬币AB

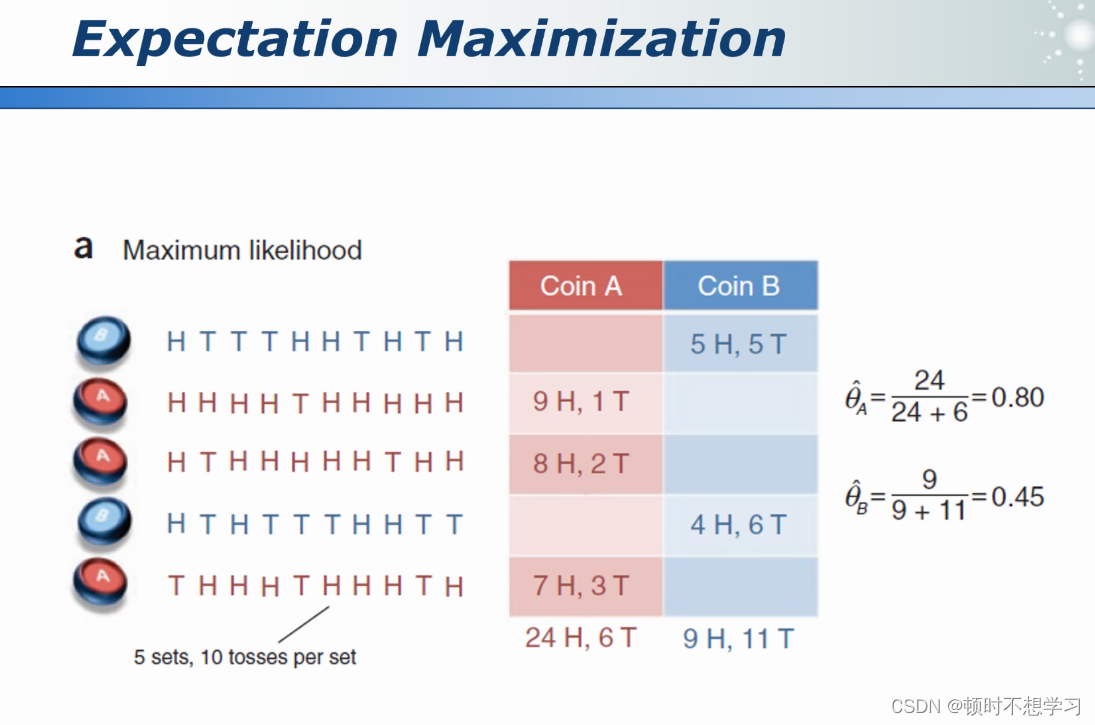
 极大似然估计   得出 A 硬币 正面朝上的概率是0.8

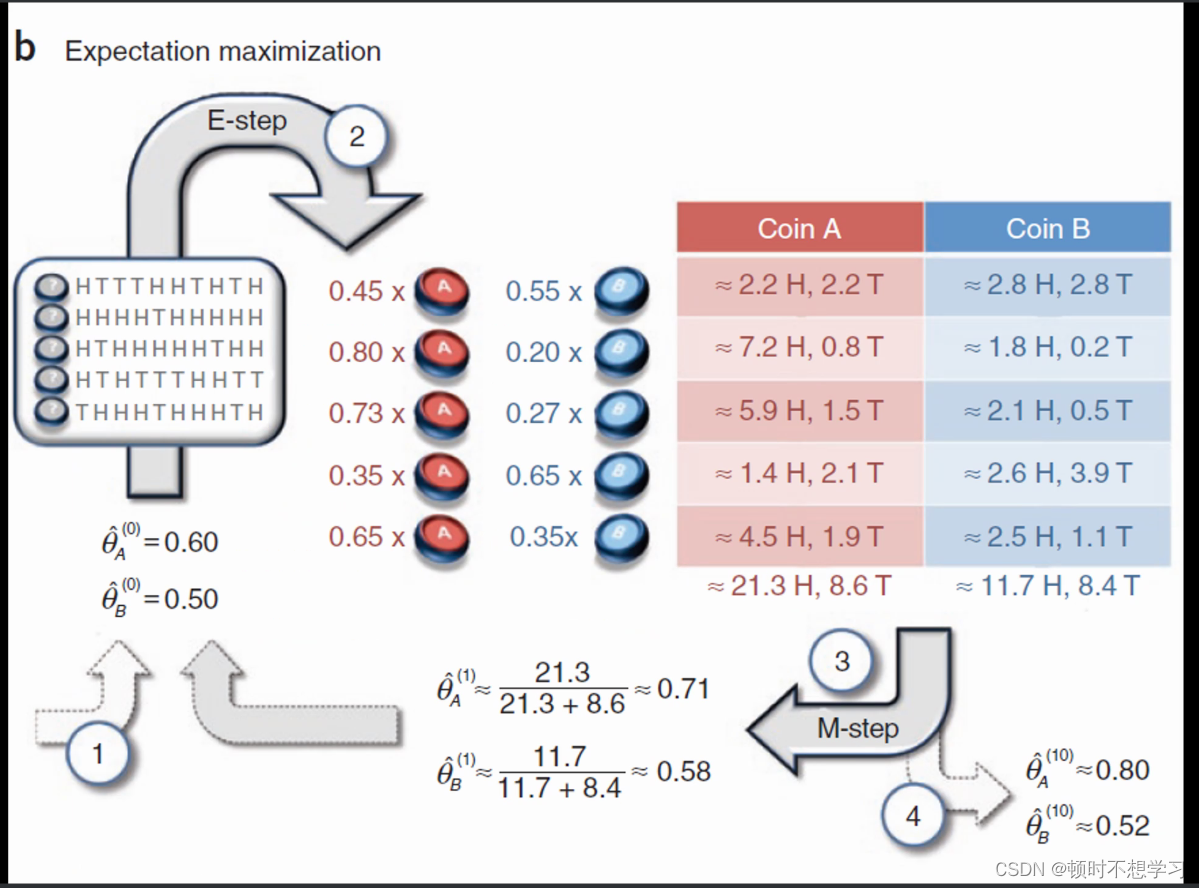
 先假设 A硬币头朝上的概率是0.6 B 0.5  

最大期望法 EM算法 高斯混合模型

 

 基于密度的混合算法

DBSCAN  滴鼻司敢

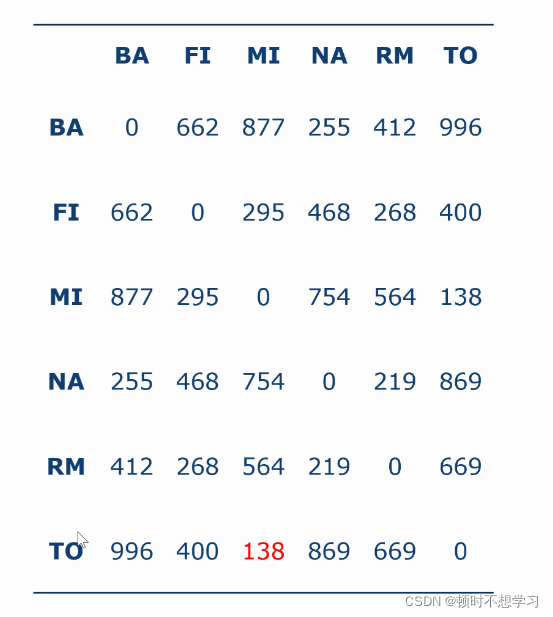
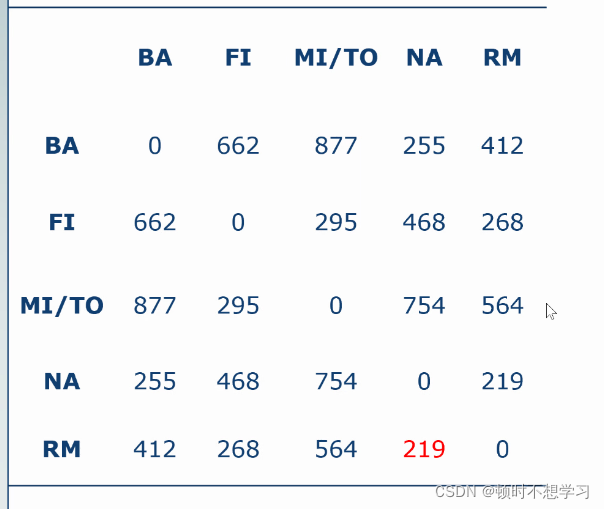
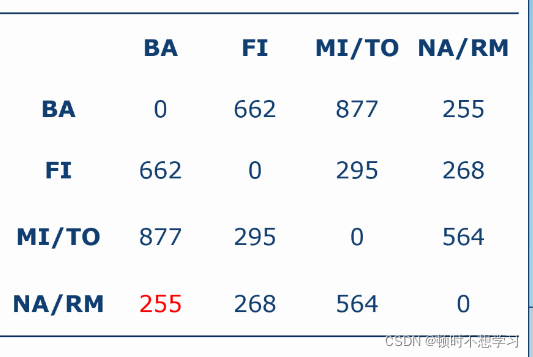
 取最小的点