轻量级节能计算卸载方案

移动边缘计算中的一种轻量级节能计算卸载方案

摘要

移动边缘计算（MEC）通过将计算任务卸载到附近的服务器，已成为移动云计算（MCC）在计算密集型移动任务上的替代方案。然而，要在低时间复杂度的前提下，综合考虑能耗和时间延迟来生成最优的卸载方案并非易事。本文提出了一种轻量级节能计算卸载方案（LEEOS），用于对任务中的每个组件进行卸载决策。首先，LEEOS计算所有组件在本地执行和远程执行情况下的成本值；基于这些成本值，采用贪心启发式方法确定哪些组件应卸载至移动边缘服务器执行。实验结果表明，我们所提出的方法在用户设备的能耗以及计算时间方面均表现出良好的前景。

CCS 概念

• 网络 → 云计算; 移动网络;
• 计算理论 → 数学优化。

关键词

节能，轻量级，部分卸载，移动边缘计算

1 引言

越来越多的新兴移动应用，如移动物体识别、物联网（IoT）数据流处理、增强现实和自然语言处理，正变得日益复杂，通常需要密集的计算。这些问题导致了高能耗[3, 13]。然而，移动和可穿戴设备（下文称为用户设备（UE））由于计算能力和电池电量有限，无法承担执行计算密集型应用所需的计算负载。

移动云计算（MCC）有望解决上述问题。然而，用户设备到云服务器的长距离传输可能导致延迟波动并增加额外的传输能量成本[7]。因此，MCC中的计算卸载并非一种有效的解决方案。作为一种替代方案，移动边缘计算（MEC）利用位于分布式网络边缘且靠近用户设备的小型但功能强大的服务器来处理计算密集型工作负载，而不是使用核心网络中的服务器。因此，MEC可以提高计算卸载效率。

关于计算卸载的研究工作通常分为两类：完全卸载和部分卸载，旨在提升用户设备（UE）的性能。在完全卸载中，任务的所有计算都在移动边缘服务器（MES）上执行，这方面的研究已在[2],[5],[6],[9]和[10]中得到广泛研究。这些方法假设服务器具有无限的计算能力且网络条件恒定。然而，由于移动边缘服务器（MES）的计算能力有限，这些假设无法实现。

相比之下，部分卸载仅动态地将任务组件的子集卸载到 MES[14]。通过智能选择最优的组件进行卸载，部分卸载可以避免不必要的数据传输开销，同时降低延迟和整体能耗。

先前的部分卸载研究工作存在两个主要问题。其一是成本函数不完善，未考虑所有重要参数，包括能耗、网络条件、计算负载、数据传输量以及通信延迟[4, 12, 14]。余等人[12]提出了一种用于部分卸载方案的深度学习方法。然而，该方法的成本函数未考虑用户设备的能耗，而由于用户设备电池容量有限，能耗是成本函数中一个非常重要的参数。另一个问题是，在选择最优卸载策略时，需要计算所有可能的组件集合的卸载成本，导致计算开销巨大[1, 8, 12]。Ali 等人[1]提出了一种基于深度学习的节能卸载方案（EEDOS），该方案在成本函数中考虑了上述重要参数。EEDOS训练一个深度学习网络（DNN）以替代复杂的计算过程。然而，DNN数据集的标签必须是最优策略，这就需要计算所有可能的组件卸载策略组合的成本。总共有2^N种（N表示应用程序中的组件数量）卸载策略可供选择，因此即使对于 20+个组件，EEDOS也显然不适用。不幸的是，现实世界中的移动应用程序通常包含超过20个组件。因此，在移动边缘计算中，亟需一种考虑所有重要参数且具有较低计算复杂度的高效能计算卸载方案。

本文提出了一种轻量级节能卸载方案以解决上述问题。具体而言，我们设计了一种简单的算法，通过判断任务中每个组件是否应被卸载，直接生成卸载策略，而无需使用最优卸载策略数据集训练深度神经网络（DNN），从而避免了对标签进行穷举计算的需求。我们将所提出的方法称为LEEOS（轻量级节能卸载方案）。在每个任务组件的执行过程中，我们的成本函数考虑了所有关键参数。所提方案不仅能提高计算卸载的能效，还能降低计算复杂度。具体而言，本文做出了以下主要贡献：

• 我们研究了移动边缘计算中的计算卸载问题，并提出了 LEEOS，一种部分卸载算法，用于决定哪些组件需要被卸载。与最先进的研究相比，该简单算法将制定最优卸载策略的计算复杂度从O(2^N)降低至O(N)。此外，我们的方法避免了深度学习中训练泛化能力差的问题，因为任务划分后组件数量的变化会导致DNN重新训练[1, 12]。
• 我们通过仿真评估 LEEOS 的性能。实验结果表明，与具有指数级复杂度的 EEDOS [1] 相比，LEEOS 在能耗和总成本方面均优于 EEDOS，且计算时间可忽略不计。

本文的其余部分组织如下：第二节描述了问题建模、成本函数和优化。第三节提供了Q值矩阵计算和最优卸载方案生成的算法设计。第四节展示了性能评估。最后，第五节总结了我们的工作。

2 问题建模

本节描述问题建模。在我们提出的工作中，我们考虑了总能耗以及延迟。该问题已被 Ali 等人 [1] 描述过。为了清晰起见，我们重新陈述问题如下。

我们考虑单个用户，并假设任务组件按顺序执行。在部分卸载中，用户设备的任务被划分为多个组件。每个组件可以在本地执行或卸载到移动边缘服务器，如图1所示。根据[11],多个组件之间的关系可以表示为一个线性有向图 T=(C, D)，其中 C表示组件集合，D表示从一个组件传输到下一个组件的数据。设 T的边由dc,c+1(dc,c+1 ∈ D) 表示。它代表组件 c和 c+1之间传输的数据。显然dc,c+1是 (c+1)的输入数据以及组件 c的输出数据。如果组件 c在用户设备本地执行，则执行 c的完成时间为：

$$
T_l(c) = \frac{W_c}{f_u} \tag{1}
$$

其中 $W_c$ 表示组件 $c$ 的工作负载，表示为 $W_c = Vd_{c−1,c}$。V表示微处理器每字节执行的时钟周期数。$f_u$ 表示用户设备（UE）的CPU速率。执行组件 $c$ 的能耗用 $E_c$ 表示。$E_c$ 假设与组件 $c$ 的工作负载成正比。

组件c也可以卸载到MES进行执行。根据假设[1]，传输带宽被划分为N个子载波。令n（n ∈ {1,2,3,…,N}）表示在每个组件执行周期内将被分配的可用子载波。类似地，m（m ∈ {1,2,3,…,M}）表示在MES上执行一个组件时将使用的CPU核心数，其中M是可用CPU核心总数。当m= 0时，表示MES处于繁忙状态，组件c将被拒绝卸载至MES。为了简化工作，我们假设最大可实现的上下行数据速率相同，用r表示。在计算卸载过程中，用户设备由于数据传输和接收所产生的能耗与传输数据量成正比。

存在一个决策周期来决定组件是在用户设备上执行还是卸载到移动边缘服务器[1]。在每个决策周期开始时，用户设备向移动边缘服务器发送组件的输入数据和信道质量信息。随后，移动边缘服务器根据接收到的信息以及移动边缘服务器当前可用的资源，为该用户设备分配n个子载波和m个CPU核心。我们使用一个组合状态向量S来存储组件的参数，即n、m、组件的输入/输出数据d，以及执行该组件的能耗Ec。对于组件c，用户设备根据组件c的成本值做出决策pc，选择在用户设备本地执行（pc= 0）或在移动边缘服务器远程执行（pc= 1），该成本值是基于组合状态向量S分别计算本地执行和远程执行所得。例如，一个包含三个组件的任务可能具有如P=[0, 1, 0] 的决策向量（卸载方案），表示组件1和3在用户设备上执行，而组件2被卸载到移动边缘服务器。因此，用户设备的状态空间和可能的动作空间由以下给出：

状态空间：

$$
{S=(c, d, n, m, E) \in S | c \in C, d \in D, n \in N, m \in M}
$$

动作空间：

$$
P={p_c \in {0, 1}, c \in C}
$$

组件 $c$ 的成本函数 $F(S, p_c)$ 表示为：

$$
F(S,p_c) =
\begin{cases}
F_l(S), & p_c = 0 \
F_r(S), & p_c = 1
\end{cases} \tag{2}
$$

其中，$F_l(S)$ 是本地执行的成本，$F_r(S)$ 是远程执行的成本。对于 $F_l(S)$，我们考虑执行组件 $c$ 的时间延迟和能耗。可表示为：

$$
F_l(S) = \gamma_1 T_l(c) + \gamma_2 E_c \tag{3}
$$

其中 $\gamma_1$ 和 $\gamma_2$ 是成本函数的单位平衡和权重系数，通过它们可分别调整时间延迟和能耗在卸载方案中的贡献。(3)中$T_l(c)$ 表示组件c的本地执行时间（由(1)给出）。

类似地，$F_r(S)$ 可以被建模为：

$$
F_r(S) = \gamma_3[(1 - p_{c-1})T_t(d_{c-1,c}) + T_e(d_{c-1,c}) + T_r(d_{c,c+1}) + t_d] + \gamma_4[E(d_{c,c+1}) + (1 - p_{c-1})E(d_{c-1,c})] + \gamma_5 K(m) + \gamma_6 K(n) \tag{4}
$$

其中 $\gamma_3$、$\gamma_4$、$\gamma_5$ 和 $\gamma_6$ 是单位平衡和加权系数，可用于调整各参数在卸载方案中的贡献。在(4)中，$t_d$ 表示用户设备解码移动边缘服务器发送的计算结果所需的时间延迟。$p_{c-1}$ 表示前一个组件的决策。$T_t(d_{c-1,c})$ 表示组件c的输入数据$d_{c-1,c}$传输的时间延迟，其表达式为：

$$
T_t(d_{c-1,c}) = \frac{d_{c-1,c}}{r} \tag{5}
$$

如果之前的决策 $p_{c-1}=1$，意味着之前的组件已在移动边缘服务器上执行，并且移动边缘服务器具有组件c-1的输出数据$d_{c-1,c}$。我们将 $T_t(d_{c-1,c})$ 乘以$(1 - p_{c-1})$，因为我们不需要将这些数据传输到移动边缘服务器。因此，如果之前的决策是卸载到移动边缘服务器，则传输过程的延迟为零。

$T_e(d_{c-1,c})$ 表示执行组件 $c$ 的时间延迟，根据 [1] 可表示为：

$$
T_e(d_{c-1,c}) = \frac{W_c}{m f_s} \tag{6}
$$

其中$f_s$是MES的CPU速率。

$T_r(d_{c,c+1})$ 表示组件 $c$ 的输出数据 $d_{c,c+1}$ 的接收时间延迟。其表达式为：

$$
T_r(d_{c,c+1}) = \frac{d_{c,c+1}}{r} \tag{7}
$$

在(4)中，$E(d_{c,c+1})$ 表示由于接收组件c的输出数据$d_{c,c+1}$而导致的用户设备的能量消耗。$E(d_{c-1,c})$ 表示由于向移动边缘服务器传输数据$d_{c-1,c}$而导致的用户设备的能量消耗。因此，出于与传输时间延迟相同的理由，我们将该项乘以$(1 - p_{c-1})$。能量消耗$E(d_{c,c+1})$和$E(d_{c-1,c})$与要传输的数据量成正比。因此，我们使用系数ξ来表示能耗与传输数据之间的关系。

在(4)中，$K(m)$是计算资源的成本。其表达式为：

$$
K(m) = \frac{m}{M} \tag{8}
$$

且$K(n)$是无线资源的成本，由以下公式给出：

$$
K(n) = \frac{n}{N} \tag{9}
$$

我们的目标是探索任务执行的最优卸载方案。对于一个任务，我们有一个决策矩阵P，其中每个元素为$p_c$，c= 1,2,3…|C|，其中|C|表示待执行任务的组件总数，且$p_c \in {0, 1}$。因此，矩阵P的阶数为 $2^{|C|} \times |C|$。对于一个任务，共有 $2^{|C|}$ 种可能的卸载方案。这意味着矩阵P的每一行代表一种可能的卸载方案或决策向量。我们需要找到最优卸载方案$P^ $，$P^ \in P$。需要注意的是，最优卸载方案是矩阵P中具有最小成本的行向量。因此，目标函数可表示为：

$$
P^* = \arg\min_P \left( \sum_{c \in C} F(S, p_c) \right) \tag{10}
$$

显然，该问题是一个NP难问题。Ali 等人[1]提出了一种基于深度学习的卸载方案(EEDOS)来解决这一问题。他们训练一个深度学习网络(DNN)以替代其中涉及的大规模计算。然而，DNN数据集的标签必须是最优策略，而这需要计算所有可能的组件卸载策略组合的成本。总共有$2^N$种（N表示一个应用程序中的组件数量）卸载策略可供选择，因此即使对于 20+个组件，EEDOS也明显不适用。不幸的是，现实世界中的移动应用程序通常包含的组件数量超过20个。因此，MEC需要一种考虑所有重要参数且具有较低计算复杂度的节能计算卸载方案。

3 算法设计

为了解决上述优化问题，我们提出了LEEOS。该方法的第一阶段是计算Q值矩阵Q。Q的每个元素表示一个组件本地或远程执行的成本。考虑到用户设备与移动边缘服务器之间的传输过程会消耗能量和时间，因此组件c的远程执行成本具有两个取值。因此，每个组件对应三种可能的动作（a∈{0, 1, 2}）。

需要注意的是，动作a=0表示本地执行，a=1表示前一个组件 c-1在本地执行（pc−1=0）时的远程执行，而a=2也表示远程执行，但前一个组件c-1是远程执行的（pc−1=1）。显然，Q的维度仅为|C| × 3。由于第一个组件没有前一个组件，因此对于第一个组件而言，a=1的成本与a=2相同。Q值矩阵根据公式 (1–9)进行计算，具体过程如算法1所示。算法1的输入是所有组件的组合状态，输出是Q。表1给出了一个包含26个组件的任务的Q值矩阵示例。

算法1 Q值矩阵计算

需要： d, E, m, n
确保： Q值矩阵Q

当 j ≤ |组件集合| 时
    如果 j = 0 那么
        Q[j,0] ← γ₁Tₗ(j) + γ₂Eⱼ
        Q[j,1] ← γ₃[Tₜ(数据传输ⱼ₋₁,ⱼ) + Tₑ(数据传输ⱼ₋₁,ⱼ) + Tᵣ(数据传输ⱼ,ⱼ₊₁) + t_d] + γ₄[E(dⱼ,ⱼ₊₁) + E(dⱼ₋₁,ⱼ)] + γ₅K(M) + γ₆K(N)
        Q[j,2] ← Q[j,1]
    else
        Q[j,0] ← γ₁Tₗ(j) + γ₂Eⱼ
        Q[j,1] ← γ₃[Tₜ(数据传输ⱼ₋₁,ⱼ) + Tₑ(数据传输ⱼ₋₁,ⱼ) + Tᵣ(数据传输ⱼ,ⱼ₊₁) + t_d] + γ₄[E(dⱼ,ⱼ₊₁) + E(dⱼ₋₁,ⱼ)] + γ₅K(M) + γ₆K(N)
        Q[j,2] ← γ₃[Tₑ(dⱼ₋₁,ⱼ) + Tᵣ(dⱼ,ⱼ₊₁) + t_d] + γ₄E(dⱼ,ⱼ₊₁) + γ₅K(M) + γ₆K(N)
    end if
结束 while
返回 Q

在获得Q值矩阵后，我们设计了一个如算法2所示的贪心决策生成算法。对于一个任务，其核心思想是通过对每个组件进行决策，而非对整个任务进行决策，从而生成近似最优卸载方案。

算法2 最优决策生成

需要: QValue 矩阵Q，组件动作 a
确保: 最优决策P

当 j ≤ |C| 时执行
    如果 j = 0 则
        ODⱼ = argminₐ∈{0,1,2} Q[j,a]
    否则如果 ODⱼ₋₁ = 0 则
        ODⱼ = argminₐ∈{0,1} Q[j,a]
    else
        ODⱼ = argminₐ∈{0,2} Q[j,a]
    结束 if
    如果 ODⱼ = 0 那么
        Pⱼ = 0
    else
        Pⱼ = 1
    结束 if
结束 while
返回 P

根本原因在于，枚举所有可能的卸载方案以找到最优卸载方案需要大量的计算，当|C| ≥ 26时无法实现。组件c的决策可以通过在Q值矩阵中选择成本最小的动作来获得。算法2借鉴了强化学习(RL)的优势，旨在每个离散状态下寻找最优策略，以最大化期望折扣奖励的总和。执行的任务可被视为一个智能体，任务的每个组件在强化学习中为离散状态，本文中的成本即为奖励。不同的是，我们的目标是最小化成本。因此，我们考虑通过寻找每个组件的最优卸载决策来生成任务的近似最优卸载方案。组件c仅有三种状态。如果a=0，则组件c将在用户设备上本地执行，且p_c=0；否则组件c将被卸载到移动边缘服务器，且p_c=1。a与p_c之间的映射关系已在Q值矩阵计算算法的设计中说明。算法2的输入是Q值矩阵，输出是一个节能且近似最优的卸载方案，表示为行向量P。算法2的时间复杂度为O(|C|)，与EEDOS相比可以忽略不计。

4 评估

本节评估了我们方法的性能。所有实验均在英特尔酷睿 i5‐5200U处理器@2.2GHz上使用Jupyter笔记本完成。假设组件间传输数据量（d）、组件在用户设备上执行的能耗（Ec）、子载波数量（n）以及移动边缘服务器中可用CPU核心数（m）服从均匀分布：d ∈ [100, 500]，Ec ∈ [1, 100]，n ∈ [1, 256]，和 m ∈ [1, 16]。所有这些随机变量对于不同的组件是相互独立的。

通过复杂的数学模型计算出的最优卸载方案[1]被用作基准，以评估EEDOS和LEEOS的性能。EEDOS采用具有2个隐藏层的深度学习网络来计算卸载方案，每层包含64个神经元。如前所述，由于标签的用于训练DNN的样本必须是最优的，该方法需要计算所有可能卸载方案的成本。生成样本标签的时间复杂度为 2^|C|。评估的指标包括决策时间、平均能耗和平均成本比率（成本比率表示为值的百分比，通过将EEDOS/LEEOS的成本与最优方案的成本之差除以最优方案的成本计算得出）。表2提供了本文中使用的各种成本参数。所使用的大多数参数与[1]相同。

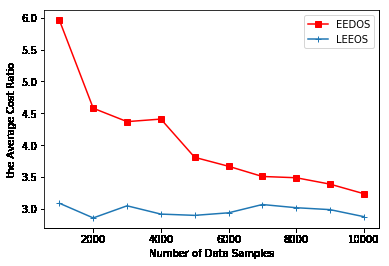
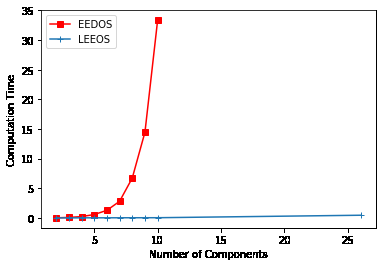
图2显示了EEDOS和LEEOS生成任务样本标签的计算时间随任务组件数量变化的对比。如图所示，EEDOS的计算时间随着组件数量的增加而指数级增长。更严重的是，我们在实验中发现当组件数量超过26时，EEDOS无法输出解决方案。然而，LEEOS的计算时间相比EEDOS要短得多。这是因为我们在组件级别上做出最优决策，以寻找近似最优卸载方案，而不是考虑每个任务中所有组件组合来获得最优卸载方案。

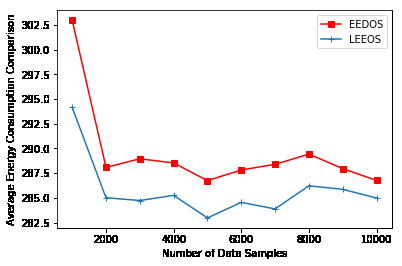
图3和图4分别展示了针对不同数量的数据样本和不同数量的组件执行任务的成本比率的平均值比较。LEEOS执行任务的整体成本低于EEDOS。

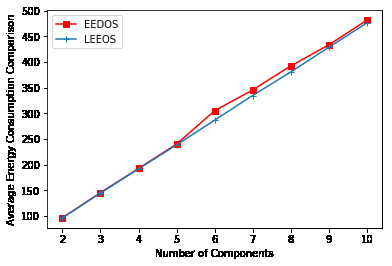
评估决策策略的一个重要参数是整体任务执行所消耗的能量。图5和图6分别显示了针对不同数量的数据样本和不同数量的组件执行任务的平均能耗。与EEDOS相比，LEEOS执行任务时的能耗更低。

5 结论

本文研究了移动边缘计算中的计算卸载问题，并提出了 LEEOS，一种轻量级的能量高效计算卸载算法，用于决定哪些组件需要被卸载。LEEOS首先计算Q值矩阵，然后采用贪心启发式方法生成卸载决策。实验结果表明，与最先进的研究[1]相比，所提方案不仅能提高计算卸载的能效，还能降低计算复杂度。