C++ 大数字相加 —— 按位相加

最新推荐文章于 2024-02-05 20:43:17 发布

原创最新推荐文章于 2024-02-05 20:43:17 发布 · 1.6k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

这篇博客介绍了如何处理两个长度不超过1000的整数相加的问题，由于超过了long long类型的范围，因此采用原始的加法运算方式。从末位向前依次相加，遇到进位则向前一位进位。博客提供了详细的C++代码实现，包括数据输入、按位相加、进位处理和结果输出。整个过程遵循从低位到高位的计算逻辑，确保正确计算超长整数的和。

问题

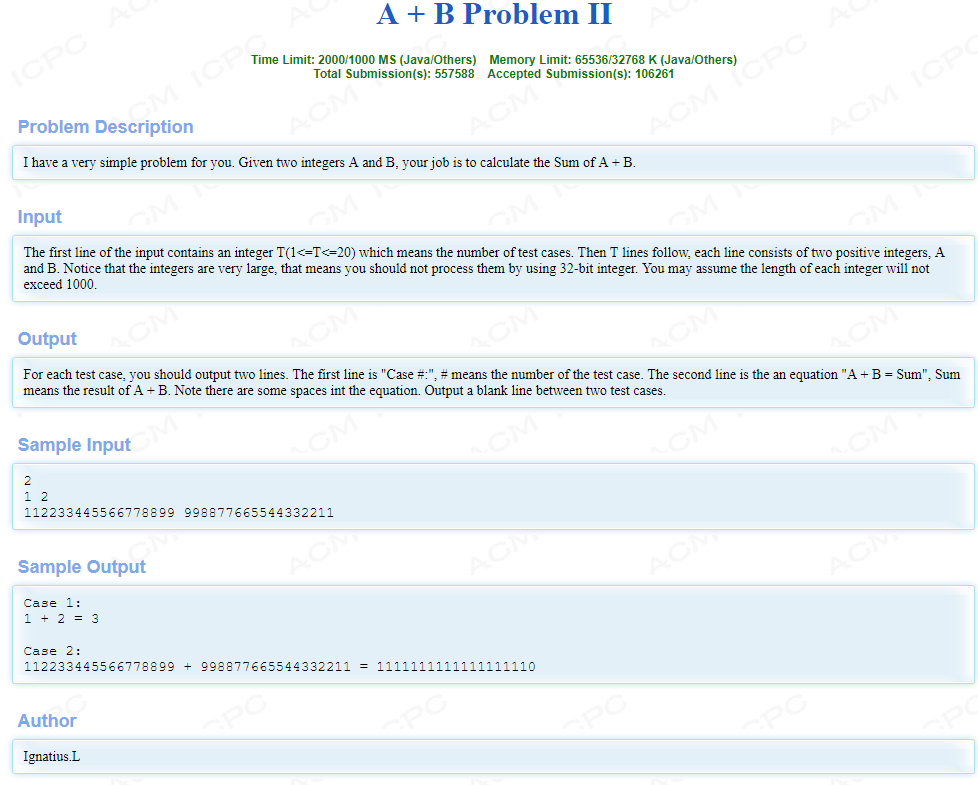
这是一道来自hdu OJ的题目

思考

题目中指出，两个整数的长度小于等于1000。显然超出了long long类型的范围。

让我们回到最原始的加法运算

通过上面这个案例我们可以总结出如下规则

从末位向前依次相加
相加结果大于十进位

现有数a与b，a有m位数，b有n位数

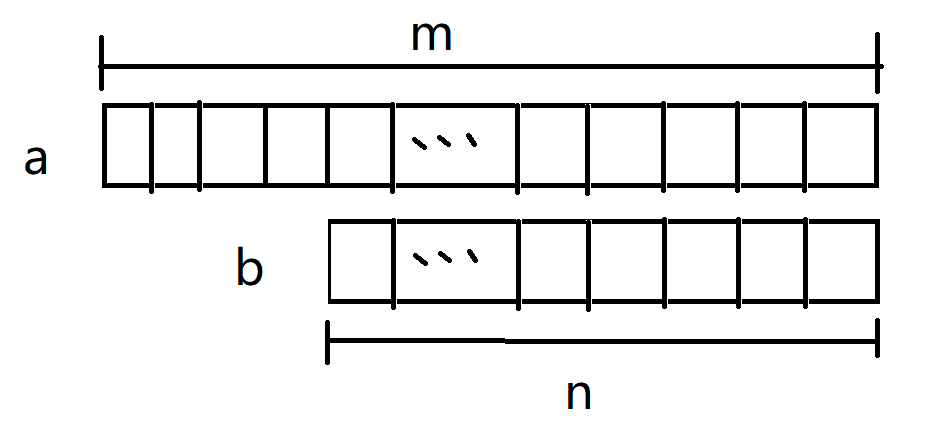
求a与b的和，首先对a与b的后n位数进行按位相加
对第零位到第m-n位进行进位

实践

数据输入

string a, b;
cin >> a >> b;

int lena = a.size();
int lenb = b.size();
int lenmax = lena > lenb ? lena : lenb;
int lenmin = lena < lenb ? lena : lenb;
int flag = 0;	//进位标志
sstream str;	//结果

定义转成int型数据的宏

#define ctoi(x) (x-'0')

从最后一位到倒数第n位按位相加

for (int i = -1; i >= (0 - lenmin); i--) {
	int sum = ctoi(a[lena + i]) + ctoi(b[lenb + i]) + flag;

	if (sum >= 10)
	{
		sstr << sum - 10;
		flag = 1;
	}
	else
	{
		sstr << sum;
		flag = 0;
	}
}

从倒数第n+1位到倒数第m位进行进位

for (int i = 0 - lenmin - 1; i >= (0 - lenmax); i--)
{
	int sum = ctoi((lena > lenb ? a : b)[lenmax + i]) + flag;
	if (sum >= 10)
	{
		sstr << sum - 10;
		flag = 1;
	}
	else
	{
		sstr << sum;
		flag = 0;
	}
}

m位数与n位数相加可能会得到m+1位数

if (flag == 1)
{
	sstr << flag;
}

输出结果

string res = sstr.str();
reverse(res.begin(), res.end());

cout << a << " + " << b << " = ";
cout << res << endl;

源码

源码尽在Github