正则化的目的
平衡训练误差与模型复杂度的一种方式,通过加入正则项来避免过拟合(over-fitting)
结构风险最小化(SRM)理论
经验风险最小化 + 正则化项 = 结构风险最小化
经验风险最小化(ERM),是为了让拟合的误差足够小,即:对训练数据的预测误差很小。但是,我们学习得到的模型,当然是希望对未知数据有很好的预测能力(泛化能力),这样才更有意义。当拟合的误差足够小的时候,可能是模型参数较多,模型比较复杂,此时模型的泛化能力一般。于是,我们增加一个正则化项,它是一个正的常数乘以模型复杂度的函数,aJ(f),a>=0 用于调整ERM与模型复杂度的关系。结构风险最小化(SRM),相当于是要求拟合的误差足够小,同时模型不要太复杂(正则化项的极小化),这样得到的模型具有较强的泛化能力。
机器学习中几乎都可以看到损失函数后面会添加一个额外项,常用的额外项一般有两种,一般英文称作L1-norm 和 L2 -norm,中文称作 L1正则化 和 L2正则化,或者 L1范数 和 L2范数
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。下图是Python中Lasso回归的损失函数,式中加号后面一项α∣∣w∣∣1, 即为L1正则化项
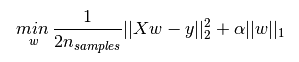

一般回归分析中w 表示特征的系数,从上式可以看到正则化项是对系数做了处理(限制)。L1正则化和L2正则化的说明如下:
L1正则化是指权值向量w中各个元素的绝对值之和
L2正





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1432
1432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








