思路
动态规划是将问题划分为互不相交的子问题,递归求解子问题,最后合并子问题的解,从而得到原问题的解。把一个复杂的问题分阶段进行简化,逐步化简成简单的问题。大事化小,小事化了。
动态规划法,它对每个子子问题只求解一次,将子问题结果保存在一个表格中,从而避免了不必要的子问题重新计算的工作。是用空间来换时间,获得的效益是很可观的。
动态规划需要经过繁琐的计算,子问题的解一旦被计算出来,就要存储起来,不要重复计算,如果你忘了这一点,你的代码将会是服务器的灾难。
通常,动态规划法用来求解最优化问题(optimization problem),如,
斐波那契数列求值问题,
钢条切割问题,
0-1背包问题,
矩阵链乘法问题,
最长公共子序列(LCS)问题,
最优二叉搜索树问题等。
大多数动态规划问题都能被归类成两种类型:
1、优化问题;2、组合问题;
步骤
动态规划算法的步骤如下:
- 刻画最优解的结构特征。
- 递归地定义最优解的值。
- 计算最优解的值,通常采用自底向上的方法。
- 利用计算出的信息构造一个最优解。
将大问题拆分成递归小问题,并用数组保存下小问题结果。
要想解决一个动态规划问题,下面的三要素是必须的:
最优子结构,
递归的边界 。
状态转移方程 。
题目
斐波那契数列求和
斐波那契数列
f(0)=0 ;
f(1)=1 ;
f(n)=f(n−1)+f(n−2) ,n≥2
前几项,就是:0,1,1,2,3,5,8,13,21,34,55,89,144,233......
它的每个数字都与前两个紧邻的数字相关。
递推公式: f(n) = f(n-1) + f(n-2) ;
这个在数学上称作【递归方程】或者【递推关系】。为了计算后面的项,它需要前面项的计算结果作为输入。
递归解法重复计算多,计算慢。
int fib(int N){
if(N == 0 || N == 1) return N;
return fib(N-1) + fib(N-2);
}
这个算法的时间复杂度为二者相乘,即 O(2^n),指数级别,爆炸。
重叠的子问题。空间换时间,避免重复计算。保存子问题的结果,避免重复计算。
int fib(int N) {
if (N < 1) return 0;
if (N == 0 || N == 1) return N;
vector<int> dp(N + 1, 0);
dp[0] = 0 ; dp[1] = 1;
for (int i = 2; i < N+1; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[N];
}
其实并不需要那么长的一个 DP 来存储所有的状态,只要想办法存储之前的两个状态就行了。
可以进一步优化,把空间复杂度降为 O(1):
int fib(int N) {
if (N < 1) return 0;
if (N == 0 || N == 1) return N;
int prev = 1, curr = 1;
for (int i = 2; i <N+1; i++) {
int sum = prev + curr;
prev = curr;
curr = sum;
}
return curr;
}
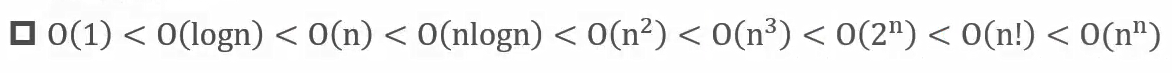





















 3029
3029

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








