Objective Function
不同于value-based methods,policy-based methods的目标是:
- 对于给定的policy:
其中θ为参数,以求找到使得policy最好的θ
那么如何衡量一个policy π的好坏呢?根据David Silver:
- 我们可以使用average value:
 (1)
(1)
- 或每个时间步得到的average reward:
 (2)
(2)
来衡量一个policy的好坏J(θ), 因此,我们的任务就是找到使得J(θ)最大的θ.
Solutions to Objective Function
对于此问题的求解,有一些不使用gradient的方法如:
- Hill climbing
- Genetic algorithms
然而,gradient-based approaches通常可以获得更高的求解效率,如:
- Gradient descent
- Conjugate gradient
- Quasi-newton
因此我们更关注gradient-based approaches。
- 设J(θ)为任意一个策略的目标函数,policy gradient method通过沿着策略梯度的方向调整θ来寻求J(θ)的局部极大值:
 (3)
(3)
其中
 即为policy gradient
即为policy gradient
下面的推导过程十分重要,后面都会用到它:
 (4)
(4)
- 考虑一个简单的one-step MDPs:
对服从d(s) 分布的初始状态s,根据一定的policy采取动作,在一个时间步后即终止动作,得到reward为:
这个问题中,目标函数为:
根据式(4),可求得policy gradient为:
- Policy Gradient Theorem
对于任意可差分的policy :
其策略梯度(policy gradient)为:
三种常用的policy gradient methods
- Monte-Carlo Policy gradient(REINFORCE)
- 采用梯度上升法更新参数
- 将第t个时间步得到的reward
作为 对
的无偏估计
算法流程如下:
我们调整的梯度,会增加positive reward的 trajectory (state-action sequence) 的概率,而减小negative reward的trajectory的概率。
那万一我们的reward全为positive呢?结果是好的坏的trajectory的概率都一起增加了,它这个样子是不行的。所以我们可以给梯度调整加个baseline b:
reward超过b的trajectory 增加概率,小于b的减小概率。
- Action-Value Actor-Critic
Monte-Carlo Policy gradient具有高方差,因此,另外引入一个critic来估计action-value function以减小方差:
其中,w为critic的参数。
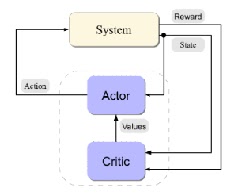
Action-Value Actor-Critic 算法中有两个机制:
- Critic:参数为 w ,估计Actor的动作价值函数
以对actor的不同(s,a)进行评价。
对参数w 的求解实际上是一个policy evaluation问题,即:
How good is policy π for current parameters θ?
有以下几种policy evaluation methods:
- Monte-Carlo policy evaluation
- Temporal-Difference learning
- TD(λ)
- Least-squares policy evaluation
- Actor:参数为 θ ,根据critic对自己动作的评价结果来更新参数θ,以使目标函数最大
假设这样一个critic:
参数为w,输出动作价值函数与输入成线性关系:
且采用TD(0) 来对policy进行evaluation:
其中,
为TD error。当TD error很小时,V(s)就趋于不变,此时policy evaluation network的参数也就趋于稳定。
采用这一critic的action-value actor-critic 的算法流程如下:
- Actor-Critic Advantage(A2C)
通过从Q(s,a)中减去一个baseline function B(s)
来减少估计的方差。因此,policy gradient可以重写为:
其中,
为advantage function。
那么,如何估计advantage function呢?下面介绍两种方法:
(1)采用policy evaluation methods(e.g. TD learning )估计
接下来即可根据下面的关系得到估计的 A(s,a)
(2)用TD error
来对advantage function进行估计,此时critic只需要一套参数v
证明:
因此可以用TD error来计算policy gradient:
-
Asynchronous Advantage Actor-Critic
-
- Trust Region Policy Optimatization
由于这个gradient是目标函数的一阶导数,所以会考虑到step size的问题,万一步子太大,更新出来的策略表现一下子下降很多,新的策略采集到的trajectory就不好,再根据这些不好的trajectory更新策略,就会变更差了吧。这样策略的variance就会很大。
为了解决这个步长问难呢,有些人就搞了个Trust Region Policy Optimization (TRPO)
arxiv.org/pdf/1502.05477.pdf
Summary of Policy Gradient Algorithms
-
Actor:
- Critic:使用policy evaluation(如MC or TD learning)来估计





 本文探讨了策略梯度方法的基础原理,包括如何定义策略的好坏,并介绍了几种常见的策略梯度算法,如REINFORCE、Actor-Critic及A2C等,同时分析了这些算法的优缺点。
本文探讨了策略梯度方法的基础原理,包括如何定义策略的好坏,并介绍了几种常见的策略梯度算法,如REINFORCE、Actor-Critic及A2C等,同时分析了这些算法的优缺点。
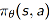
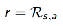
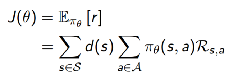
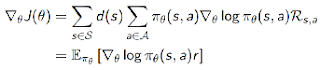

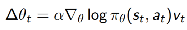
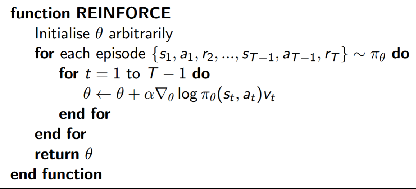
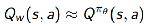
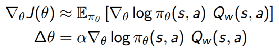
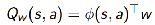
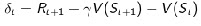

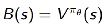
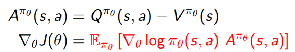
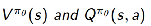
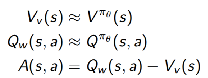
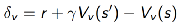
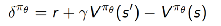
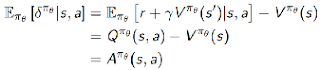
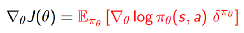

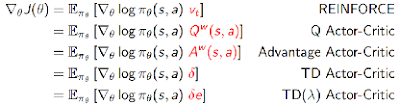
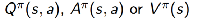
















 23
23

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








