内容来自维基百科
度盘分享 实际是以pdf保存的网页
1.定义
向量或矩阵微分类型
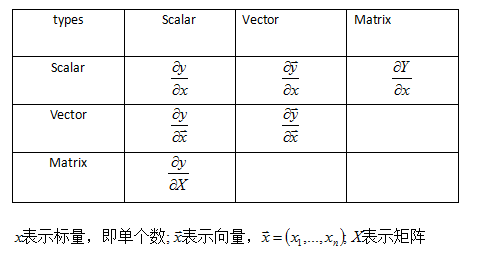
(1)Scalar - by - Scalar
实例:
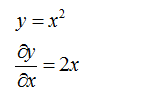
(2)Vector - by - Scalar
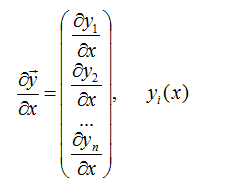
实例:

(3)Matrix - by - Scalar

实例:
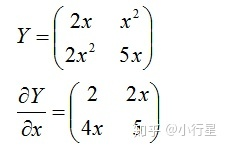
(4)Scalar - by - Vector
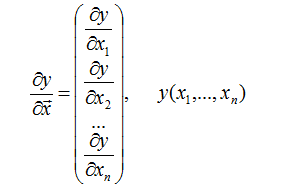
实例:
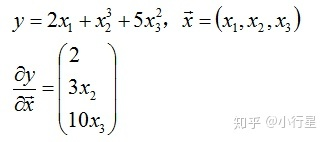
(5)Vector - by - Vector
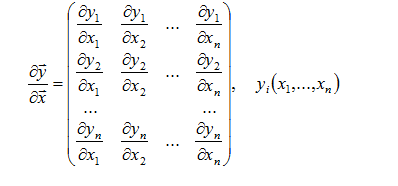
实例:

(6)Scalar - by - Matrix
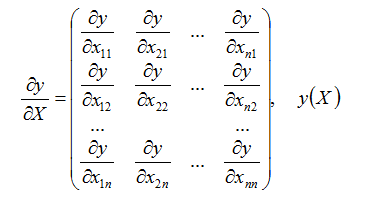
实例:
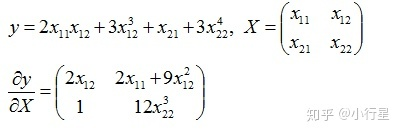
定义是十分直观的。
还可以看到- by - Scalar时,y的每个元素是关于这个标量x的函数;- by -Vector时,y的每个元素是关于Vector中所有元素的函数,当然某些元素的系数可能为0;- by -Matrix时,y的每个元素是关于Matrix中所有元素的函数。总之y的每个元素是关于x所有的元素的函数。
无论y是什么形式(标量,向量)它与x的关系都表示多维空间的一个超平面或曲面,而求一阶导的可以得到这个面上具体某点的逼近超平面。
=================================================
2.布局。
在向量或矩阵求导时的分子分母有不同组合方式,导致同一求导结果却有不同的形式,实际就是有时把求导的结果转置了,这在计算中会比较容易混淆,而又混淆后会导致后面矩阵计算的错误。
于是规定按不同组合方式称为按分子布局和按分母布局。

这里向量开始时均默认为列向量。
(1)按分子布局。分子不动,分母进行转置。
以下是按分子布局的示例
{1}

{2}

{3}

{4}

(2)按分母布局。这里分子转置,分母不动。
以下是按分母布局的示例。

比较按分子布局和按分母布局,可以看出同一个微分运算可能会因为使用不同的布局显示而得到形式上的不同结果。
=====================================================
3.各种identity(恒等式)
常见的对向量或矩阵求导并非上面的定义中的简单求导,一般都是带有系数或为复合函数,如回归中(Ax-b)^2对x求导,A为矩阵,x,b为向量。希望得到相关恒等式。以下恒等式均可以通过原始定义得到。
关于符号:若某个字母为常数则直接写为a,若为x的函数则会注明a=a(x)。数学的字母为标量,中文的字母为向量,包括函数也是这样。点乘为矩阵乘法 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,也有叉乘
,也有叉乘 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,也有张量积
,也有张量积 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,也有对应元素相乘
,也有对应元素相乘 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,主意它们各自的定义。
,主意它们各自的定义。
平常查找需要的恒等式时,先明确类型如Scalar - by - Scalar,再找对应的情况。
(1)Scalar - by - Scalar
分子是标量,Scalar - by - Scalar的结果一定是标量
[1]with vector involved
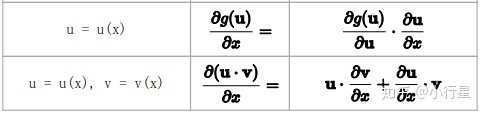
x是一个标量。u(x),v(x)为 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,这个是可以的如x
,这个是可以的如x ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) (2x, 5x)。g(x)为
(2x, 5x)。g(x)为 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) 。可以看到分子均为标量。
。可以看到分子均为标量。
[2]with matrix involved

矩阵得到标量常用的是其行列式或迹,也可以用其它函数映射为标量,上面的第4行中的g(X)为 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) 。第5行中的g(X)
。第5行中的g(X) ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,表示g(x)分别对矩阵X每个元素其作用
,表示g(x)分别对矩阵X每个元素其作用
关于行列式的求导以后再专门写吧。tr( ) 实际是求和,求导可以不用管。
(2)Vector - by - Scalar
分子是向量,Vector - by - Scalar的结果一定是向量

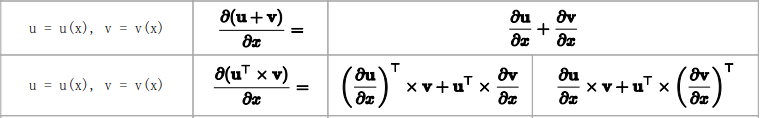
上面第二个为叉乘,不是矩阵乘法。
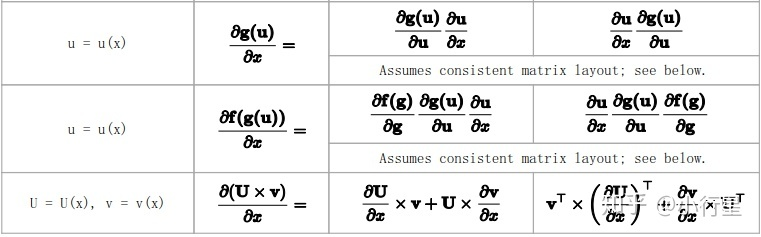
... - by - Scalar应该是较为简单的,只用把标量x依次代入到 ... 中每个元素进行求导即可。
(3)Matrix - by - Scalar
分子是矩阵,Matrix - by - Scalar的结果一定是矩阵
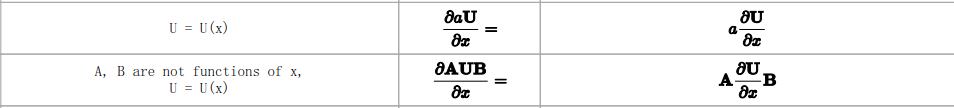

上面第3行为克罗内克积
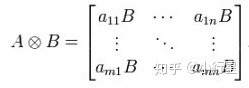
第4行表示矩阵对应位置元素相乘
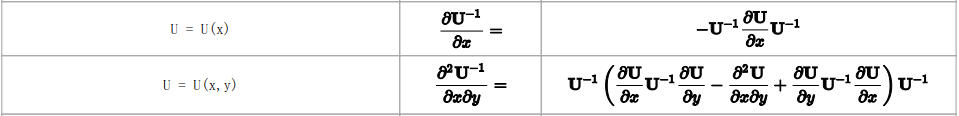

(4)Scalar - by - Vector
分子是标量,Scalar - by - Vector的结果一定是向量。
这个应该在机器学习中用得比较多,因为损失函数就是Scalar - by - Vector,Scalar为损失函数值,Vector为要估计的参数。


f,g均以数学形式写的为 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png)

注意上面两张里面的u,v一个为数学的为标量函数 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,一个为中文写的为向量函数
,一个为中文写的为向量函数 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,故结果不同。
,故结果不同。

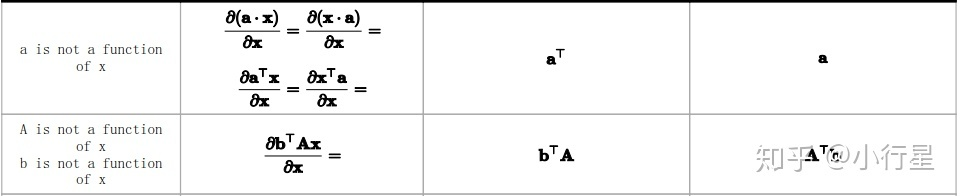




(5)Vector - by - Vector
分子是向量,Vector - by - Vector的结果一定是矩阵
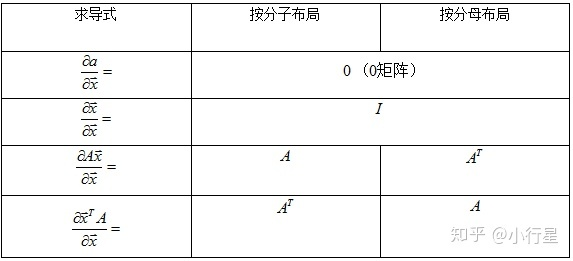
分不清结果是A还是A_{T}时,可以写个结果(1,2)位置的为a_{12}还是为a_{21}即可知。
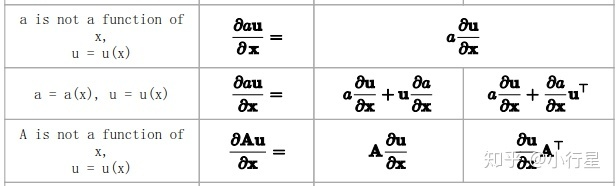


上面的a表示常数标量,a(x)表示 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) 结果为标量, u(x),v(x),f(x),g(x)表示
结果为标量, u(x),v(x),f(x),g(x)表示 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) 结果为向量。
结果为向量。
(6)Scalar - by - Matrix
分子是标量,Scalar - by - Matrix的结果一定是矩阵
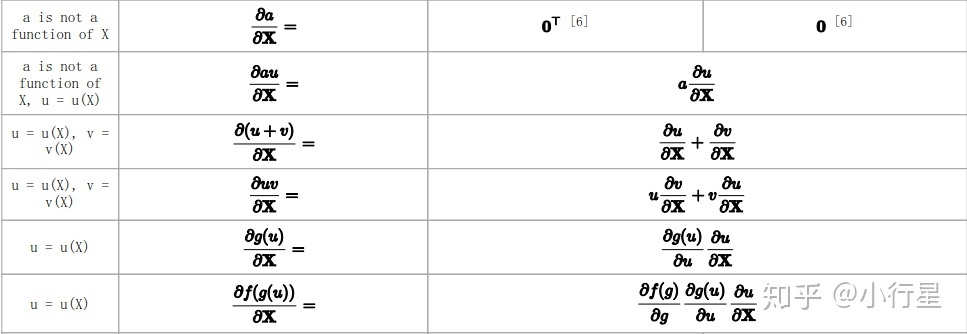

这里的g(x)为 ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png)

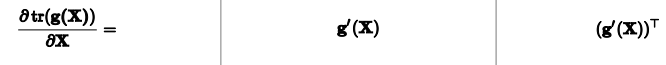
这里的g(X)表示g(x) ![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) 分别对X中每个元素起作用
分别对X中每个元素起作用




(7)other
=================================================
4.雅可比矩阵。这个用得很多,故单独来说。
(1)定义

可以看到它是Vector - by - Vector,且这里是按分子布局。
(2)雅可比矩阵用于线性逼近

(3)雅可比行列式

5.海森矩阵。上面的矩阵微分均为多元一阶微分,海森矩阵为多元二阶微分。
(1)定义

一阶导是Scalar - by - Vector,为得到列向量,使用按分母布局。二阶导是Vector - by - Vector,且是按分子布局。
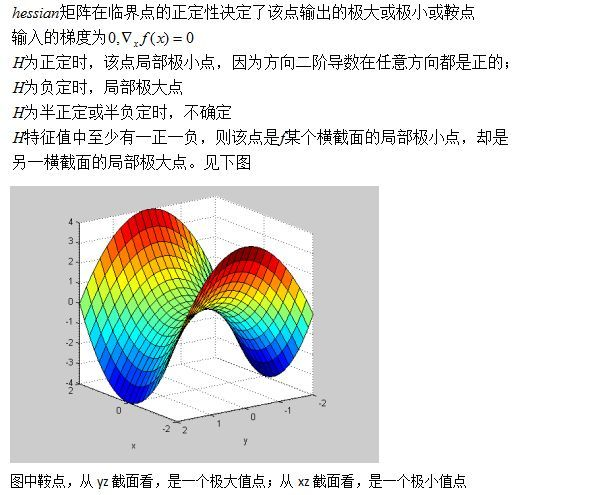
(2)判断极值





















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








