计算机速成课笔记（一）

1.小总结

这是针对B站课程《计算机速成课》的笔记，主要是1-9，剩下的会做成二，三发出来。

我认为1-9主要在讲如何做出一个具备一定计算能力的计算机，从底层的数学理论讲起，在讲各个部件，最后抽象成为一个模拟计算机。

2.计算机的底层逻辑

（1）计算机简介与历史

这方面不是很重要，主要是作为补充。

计算机的发展诚如他的名称，以计算为主。所以发展历史很漫长，人类在加快计算速度方面做了不少努力。从算盘-步进计算器-差分机（分析机）-打孔卡片制表机。

这些都是用来处理数据进行计算的，而有趣的是差分机和分析机。差分机是一个复杂的机器，他能近似多项式，甚至对一些数学函数的值进行计算（这些手算都极其麻烦），但由于太笨重和超前，当时没有建造出来。分析机也同样，但分析机比差分机高级，它被设定为不止进行特定运算的机器，甚至能根据一定的顺序执行计算，有内存。这种超前的想法对后来的计算机发展有了极大的启发。

（2）计算机的数学理论和物理基础

可能大多数人会认为我们是先在理论上思考计算机的组成再去研究各个部件怎么变为实际。但事实上并不是。计算机如果想要计算数据-----首先需要读取储存数据的，而数据在计算机的表现形式，现在大家都知道，是通过二进制储存的。但选择而二进制并不是因为它优于其他的计数法，而是因为在当时二进制的数学理论发展成熟。

首先是继电器，利用继电器是否通电导致电路的开关，从而使马达驱动进行计算。但由于机械磨损速度太快，人们迫切的需要其他的相同功能的组件代替它。于是有了二极管。这种电流只能单向流动的电子部件，磨损减少，效率提高 。但还是容易损坏，然后有了晶体管-----再一次提高效率，降低成本。

这是物理基础，然后我们利用这个，向上抽象，做出布尔逻辑和逻辑门。

我们都知道，电路只有两种运行状况。开路和短路，联系到逻辑就是--是与非，再到二进制就是0和1.

但是其实晶体管除了能导致开路和断路，同样也可以让不同大小的电流通过。所以其实也有三进制或五进制的电子计算机。但由于状态越多，信号越难区分。二进制的信号是分开的 ，只有开和关，可以尽可能地见减少这类问题。

如上面所说二进制的数学理论发展成熟--布尔代数，即利用逻辑方程 系统而正式 地证明真理。 在布尔代数中，变量的值是true和false，能够进行逻辑操作。 

布尔代数：NOT ，AND ，OR，XOR

以下是四个表格，表示他们的功能（在这里不进行物理电路上的描述，单传的作为一个逻辑抽象的小组件）

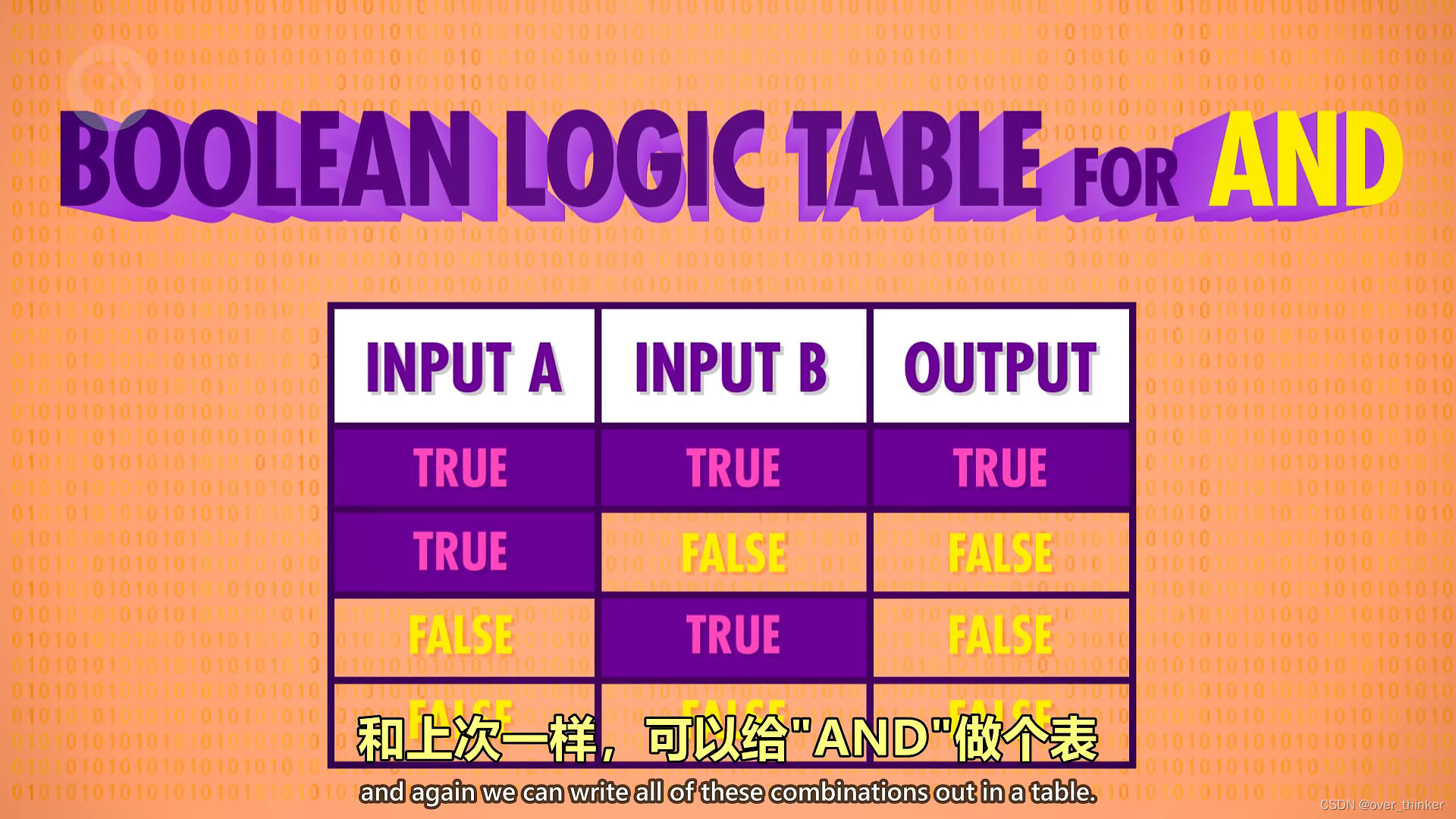
 再展示一下如何用and or not 组装nor。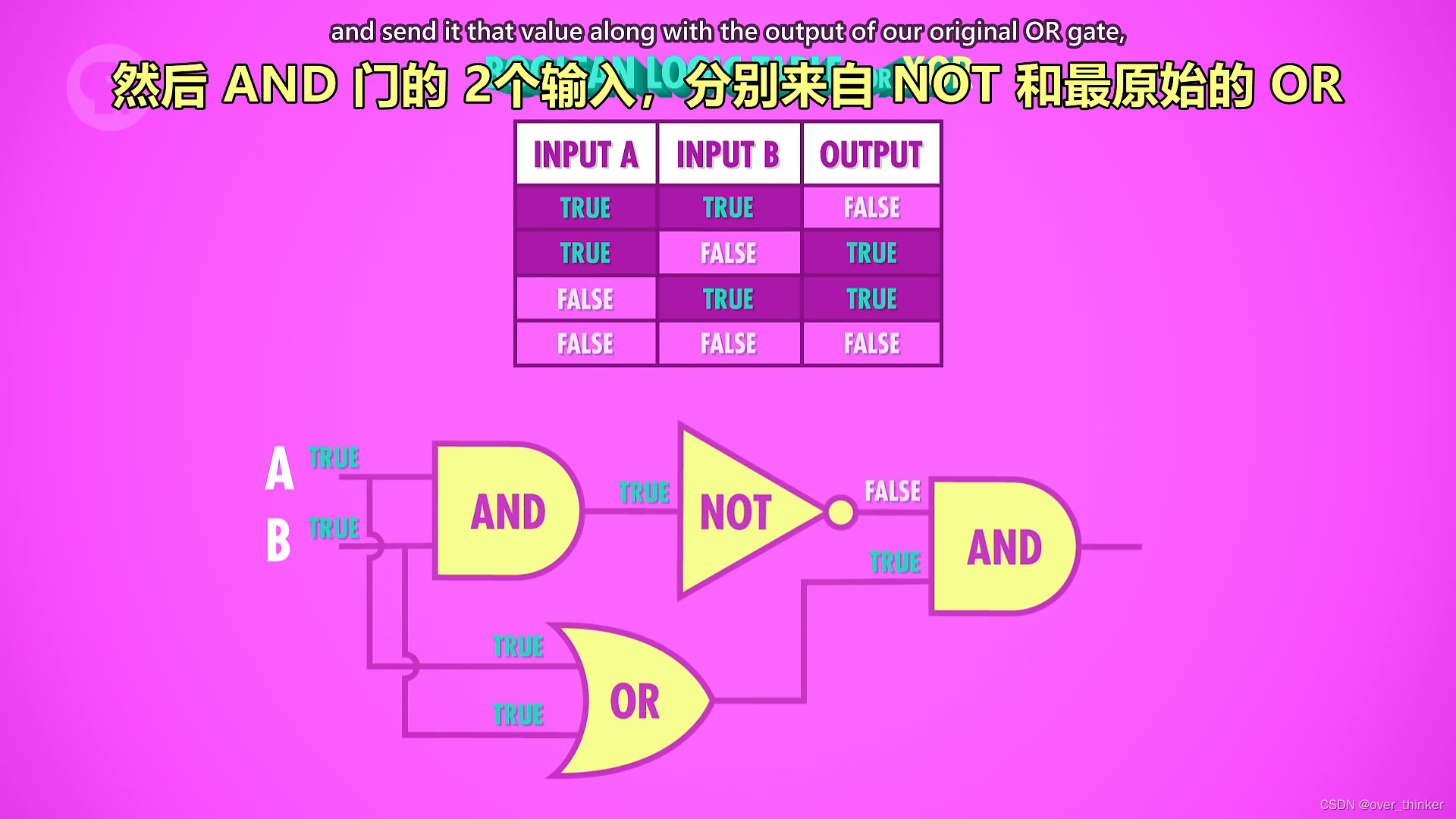

确认理解后，这是第一层抽象 。

3.计算机的部件及构成方式

二进制已经在C语言学过，在这里略过。

算术逻辑单元ALU

表达和储存数字的确是计算机的重要功能，但真正有意义的是处理数字。也就是加减乘除，阶乘等等让两个数字再被处理后变得有意义。这就是ALU，计算机的数学大脑。

那么联系上上一层的抽象，让我们利用逻辑门做出一个ALU电路。

ALU有两个单元，算数单元和逻辑单元。算术单元，字面意思，负责计算机里的数字操作。

先来考虑加法，即两个数字相加--a+b＝c

两个输入，一个输出。

在二进制里，这只有四种可能。

 将TRUE和FALSE等同于1和0，这就是个XOR逻辑门。

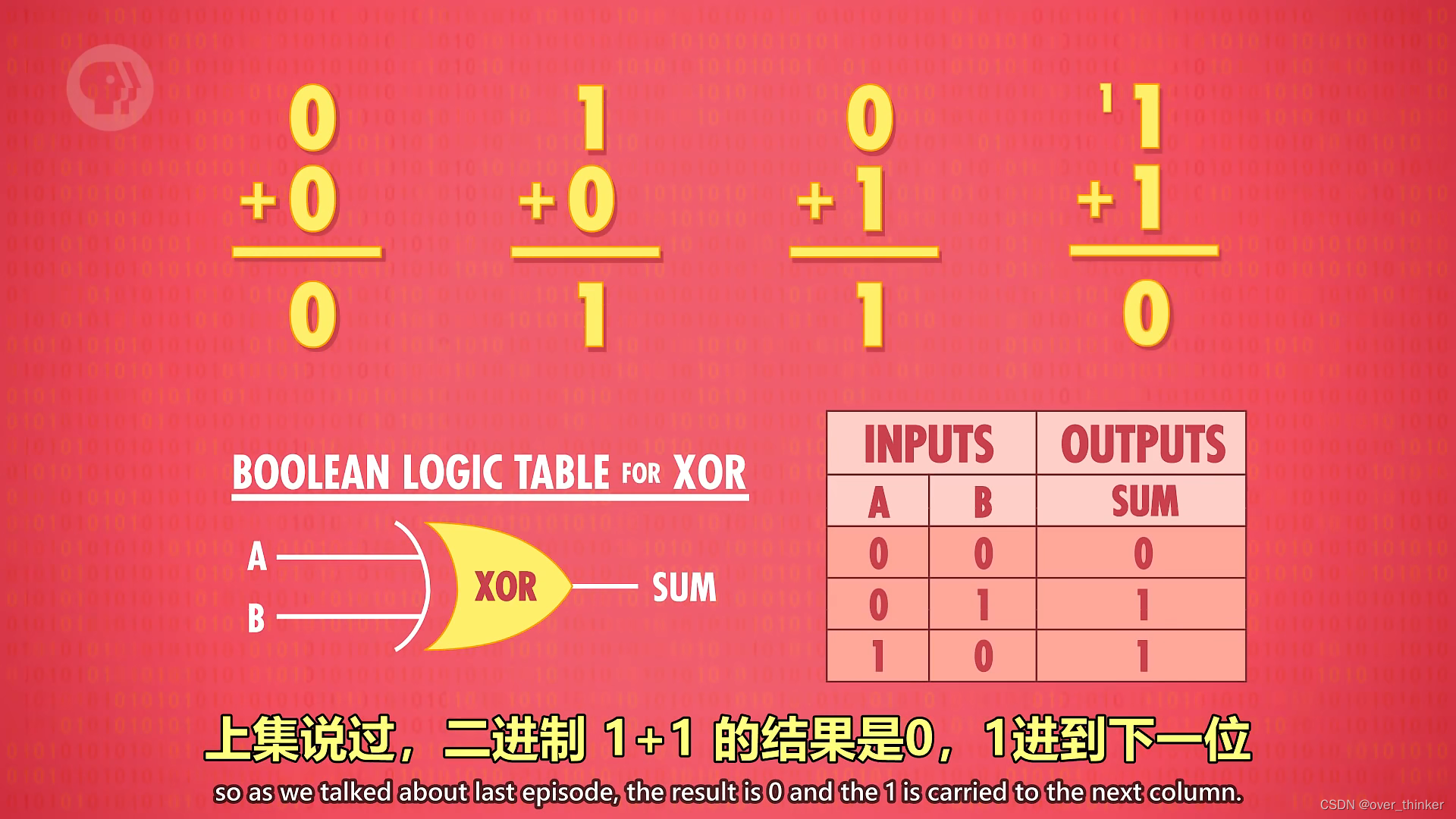
但这只有三种情况，少了一种即1+1。

1+1＝2，可是二进制里没有二。

所以1+1＝10即进一位。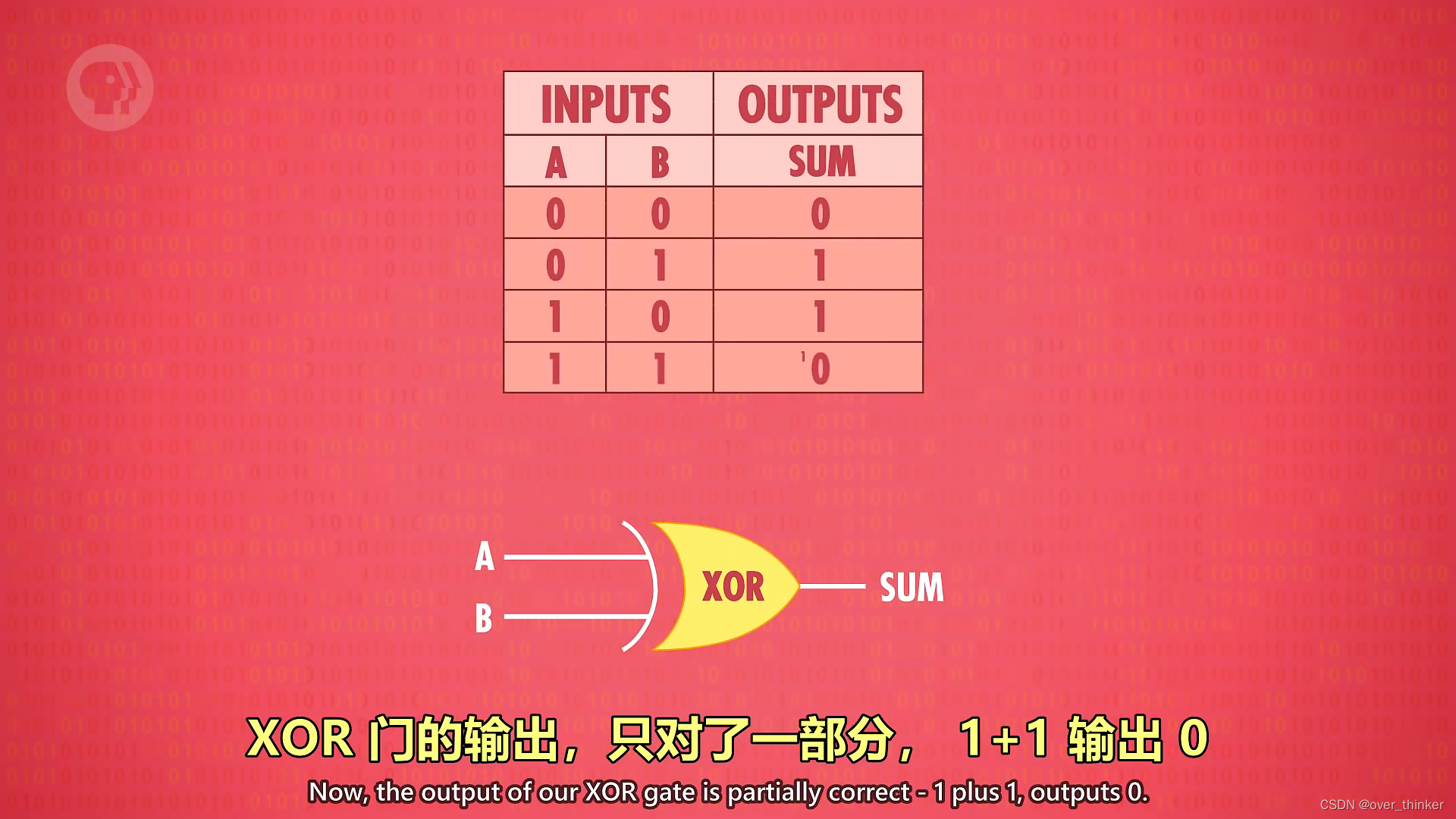

这时XOR只表示了一位即0，缺少进位，所以需要一个组件在前三张情况表示0而最后一种表示1。

是不是很熟悉？这不就是AND吗？

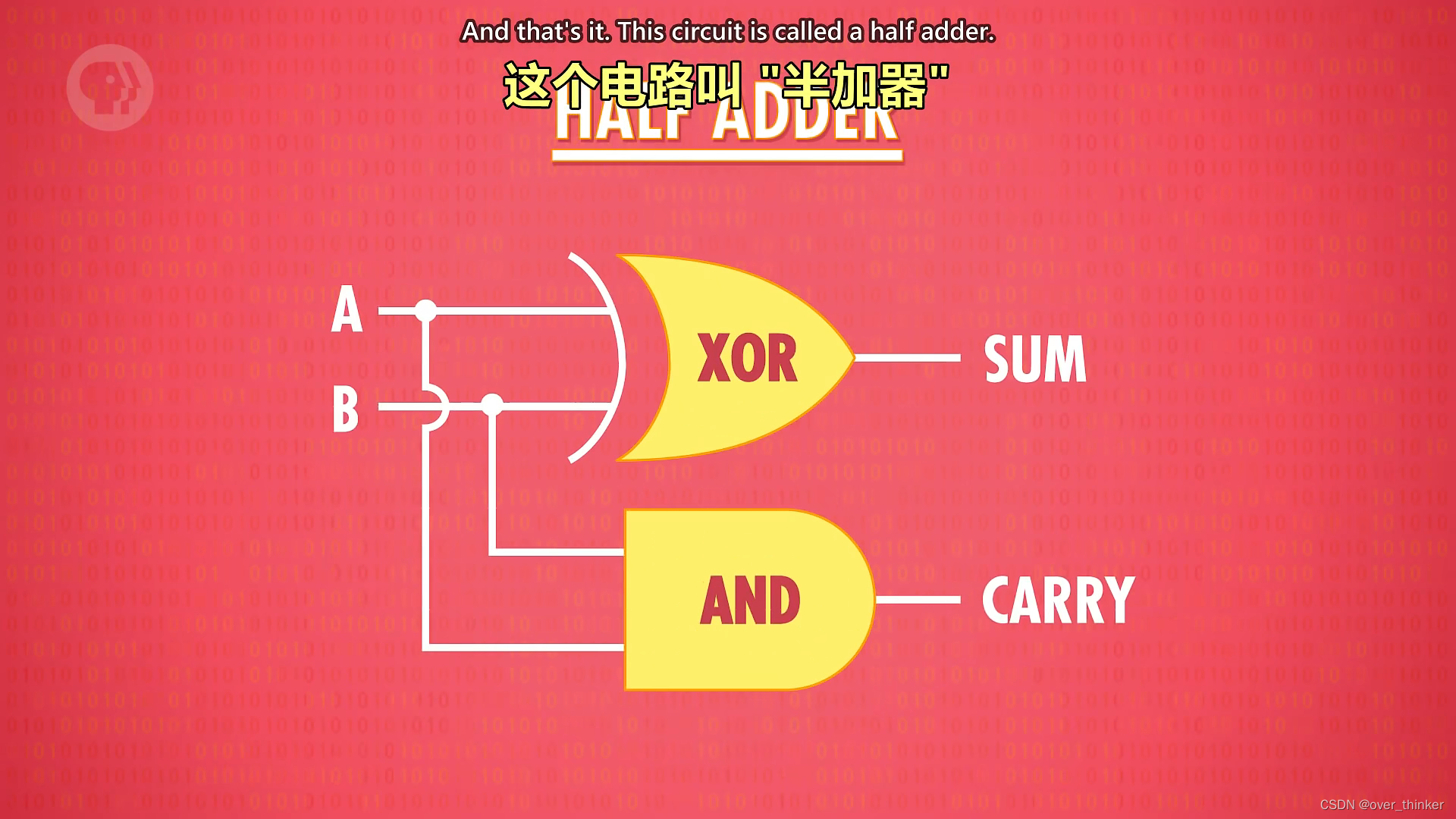
恭喜！你完成了一个加法电路，我们抽象一下，给它起个名字——半加器在那么这个电路就变成了这样。

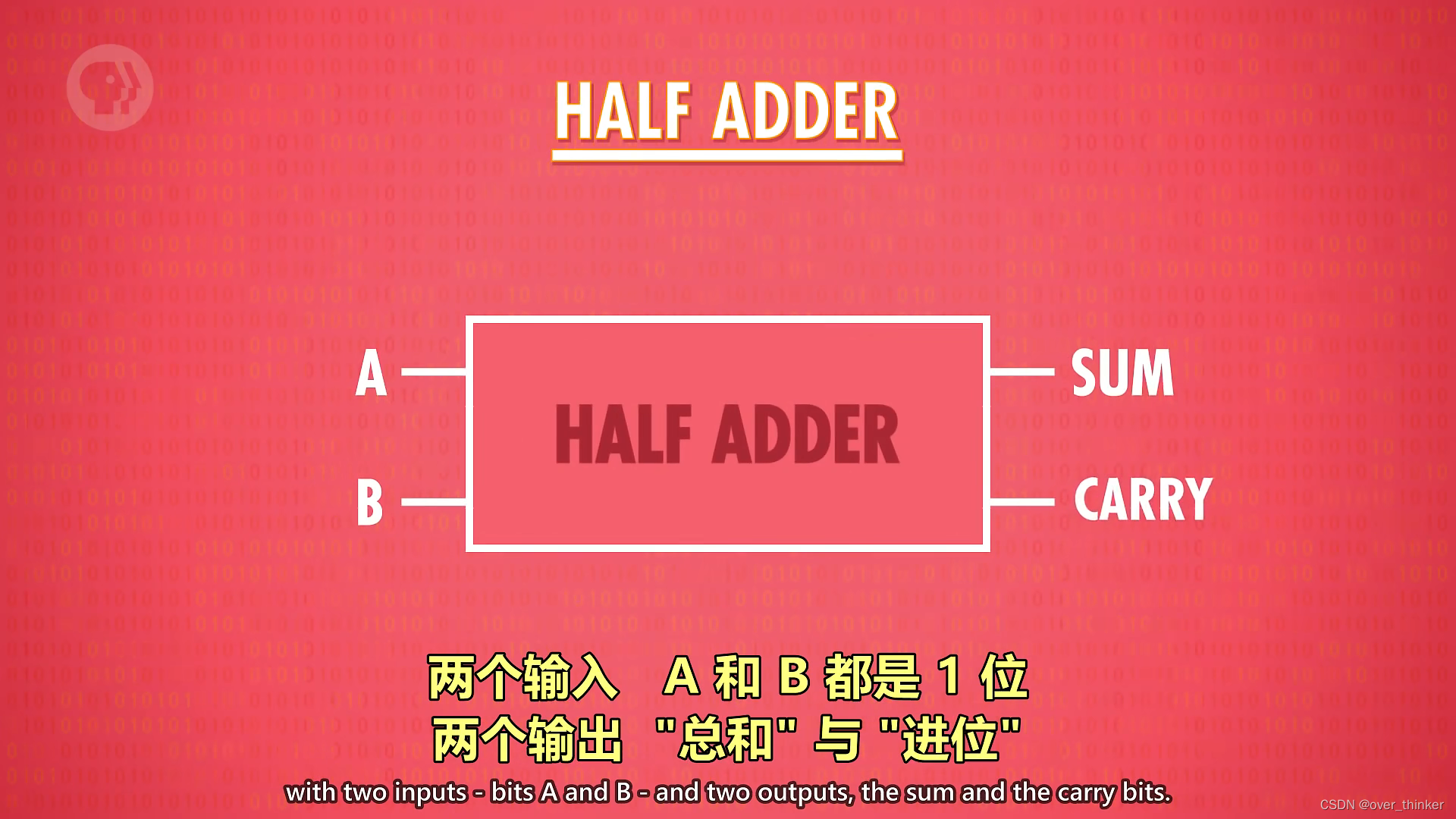
（把这个sum理解成个位，carry是十位也许更好懂——注意这只是类比，不是真的十位和个位）

但这个算术还是太少了，如果是1+1+1或者101+101呢？

这就是全加器----计算a+b＋c＝d

 

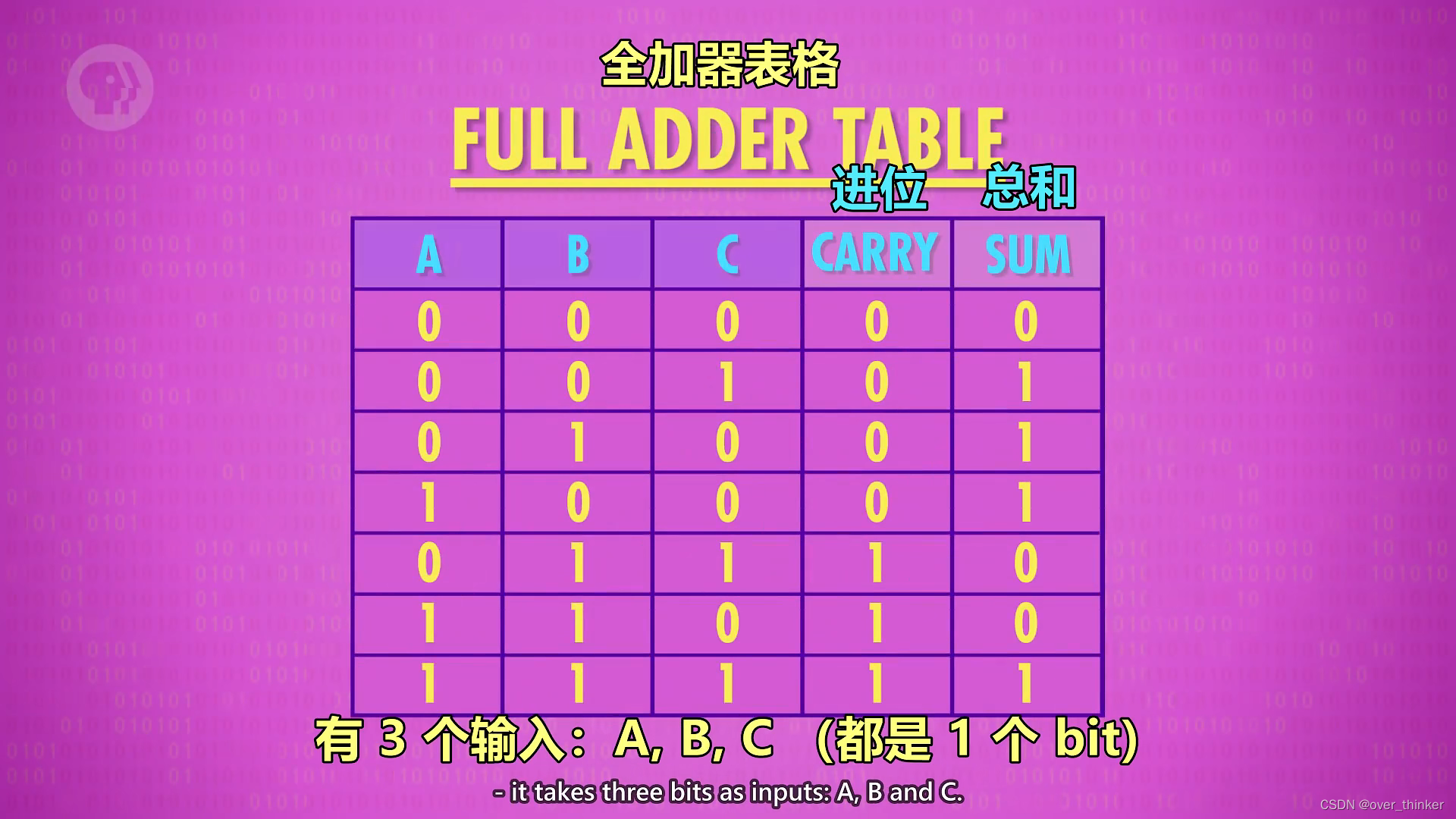
最大的为1+1+1＝3，回到上面，我们利用半加器做出全加器。

也就是先计算a＋b加这个结果视为c计算c＋d。注意进位哦～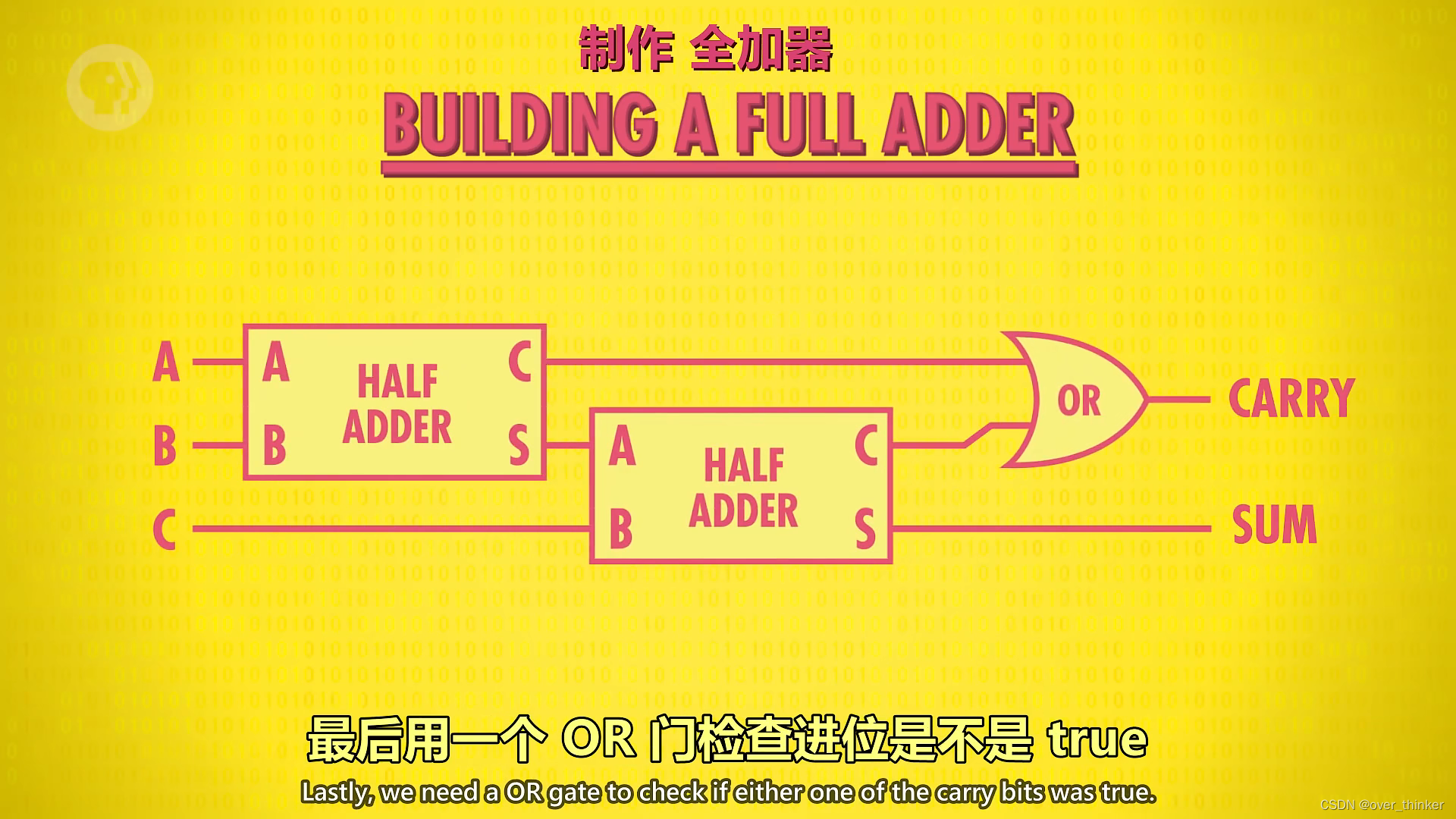

那么利用这两个组件，让我们计算一点稍微难的吧。

八位与八位相加。

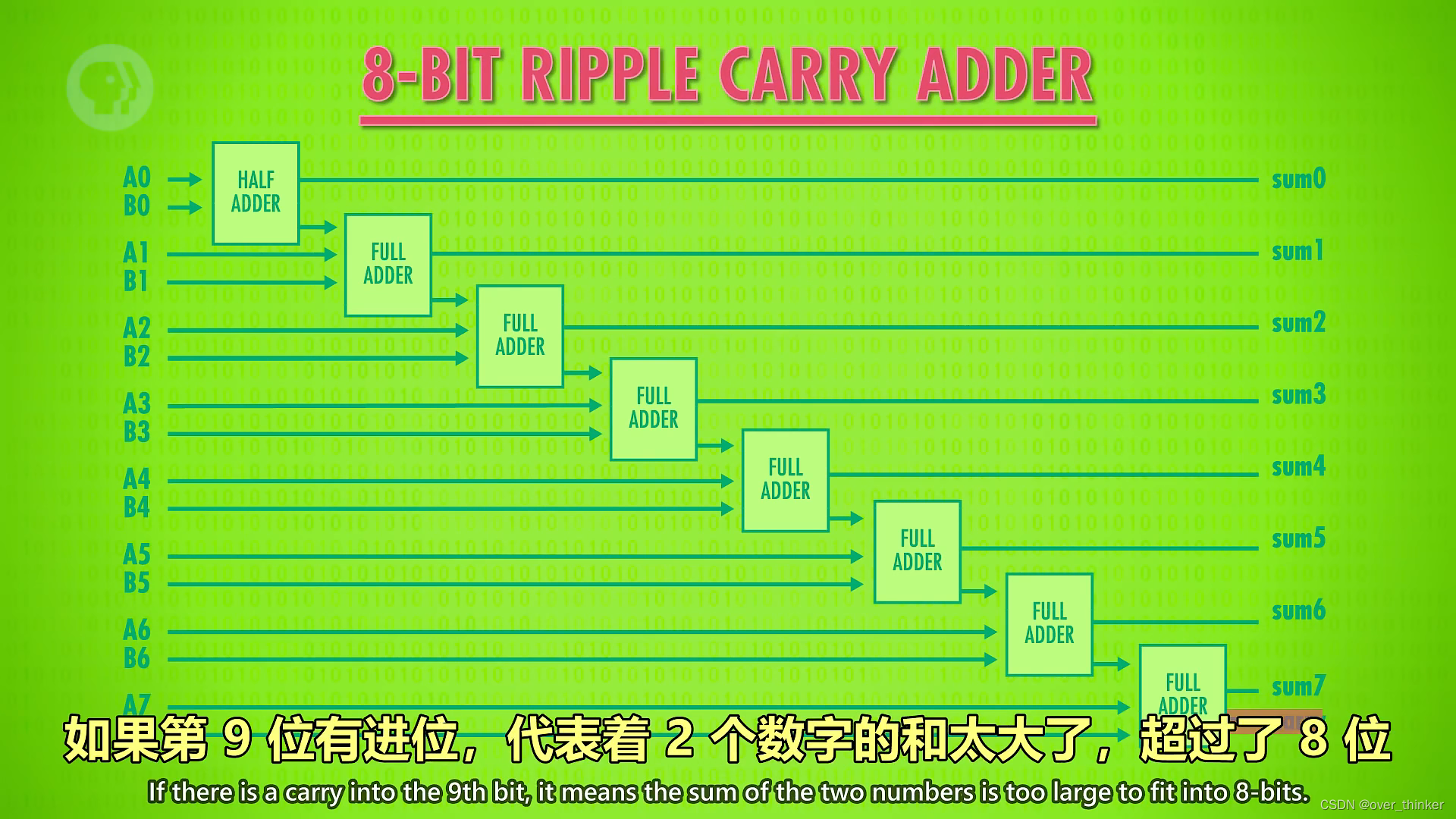
将个位，十位，百位……（注意这也是类比）分别相加。

除了第一个是半加器其他都是全加器——自己思考一下为什么。

但如果第九位也有进位，即两个八位数想加成为了九位数，由于第九位已经没有全加器处理进位导致了——溢出。

熟悉吗？C语言也有。

意味着和超过了用来表示的位数。

解决这个问题可以多增加几个全加器，增加位数，但也导致了运算时间变长。

如果是日常简单的计算，这样都增加也许并不烦人，但是面对以亿计量的计算，这样的计算导致的的延长就难以忍受。所以目前使用的是----超前进位加法器。这是ALU能做的其他计算。

你可能注意到没有乘法和除法，这是因为简单的ALU的电路把乘法变成了加法。乘法电路放在了更优秀的处理器里，用来更多的逻辑门，这就是为什么没有简单的处理器。

同样逻辑单元里，我们就直接执行逻辑门的操作，NOT AND OR XOR，甚至一些简单的数值测试，但是不重要，只要我们理解了ALU就行。

再来一层抽象！！！这里的V就是我们指的ALU，这里有三个输入。

输入两个数，和一个四位的操作代码。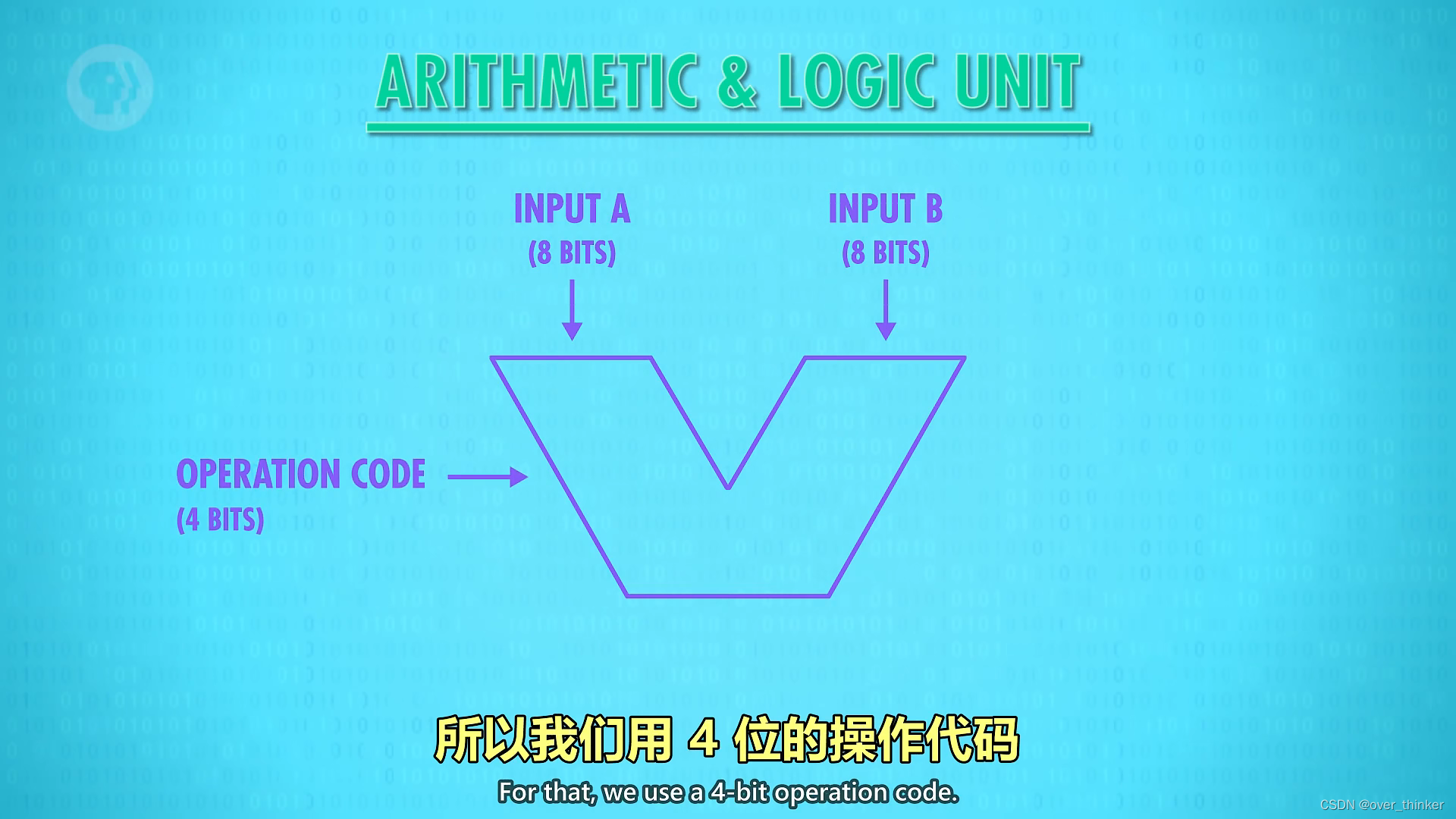

RAM寄存器和内存

如果只是处理数字而无法储存结果，那么处理就毫无意义。

在ALU里，我们可以发现所有的计算都是单向的流动的，所以为了储存它，让我们考虑一下将输出在放到输入里，看看结果如何。

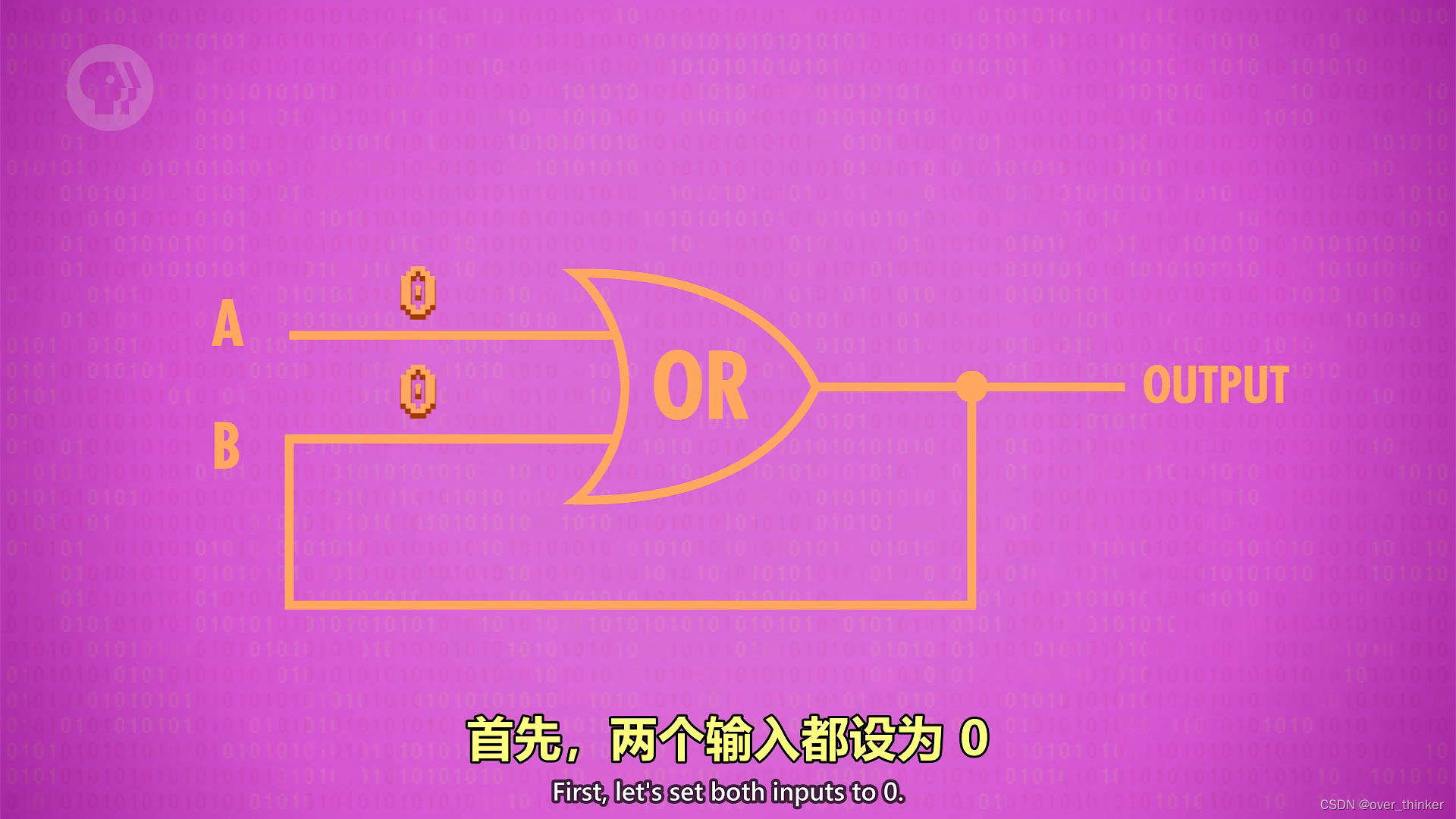
 第一次输入：0                                0                                     输出：0

                        结果回传，改变另一个输入

第二次输入：0（被回传的结果）     1                                    输出：1

                        结果回传，改变另一个输入

第三次输入：1（被回传的结果）      0                                    输出：1

                        结果回传，改变另一个输入

第四次输入：1（被回传的结果）      1                                 输出：1

 这时我们可以发现无论如何改变输入，结果都不会变了，永远都是1-----也就是说我们把1这个结果存起来了。

换到and门试一下

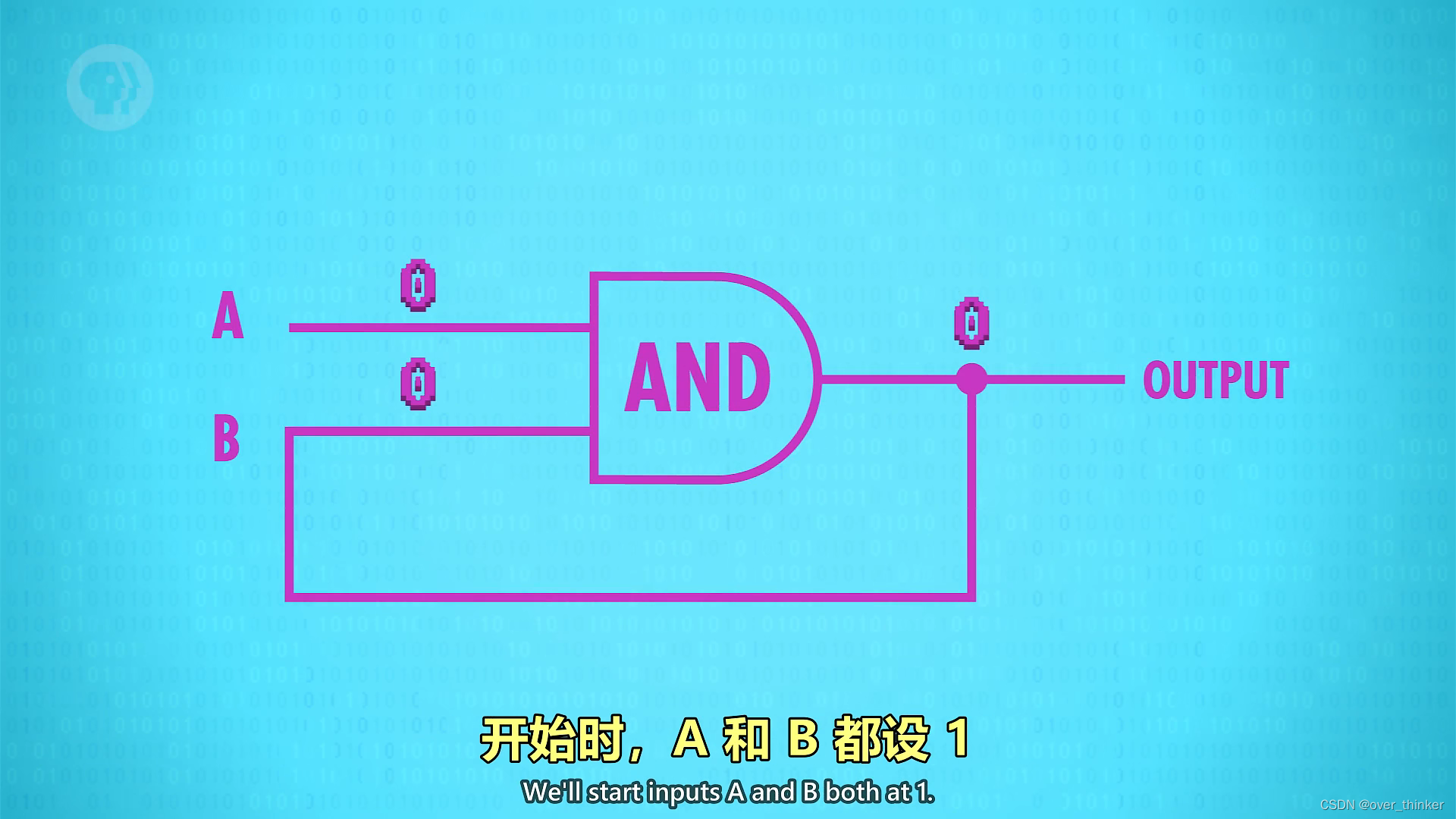
 第一次输入：1                                1                                    输出：1

                        结果回传，改变另一个输入

第二次输入：1（被回传的结果）     0                                    输出：0

                        结果回传，改变另一个输入

第三次输入：0（被回传的结果）      1                                   输出：0

                        结果回传，改变另一个输入

第四次输入：0（被回传的结果）      0                                   输出：0

 这时我们可以发现这个电路存了0------无论如何改变输入，结果都不会变了，永远都是0.

也就是说我们已经做了储存0和1的电路，别忘了，计算机的世界里就是只有0和1。

那么只要将这两个电路巧妙的组合在一起，这就是储存的方法。

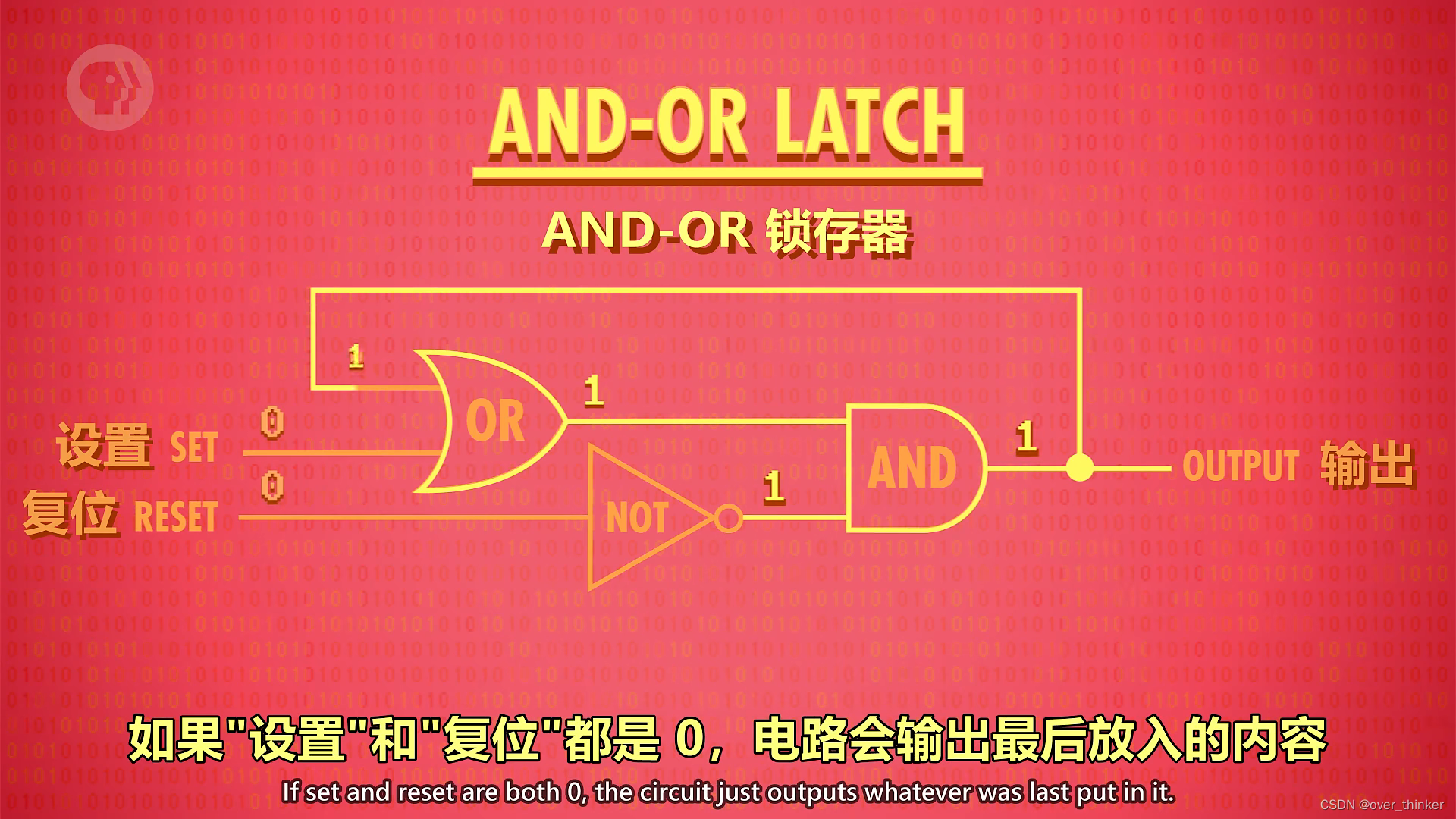
当复位为1时：      输入：0  1       输出： 0        输入：1   1       输出： 0    （锁住了0值）    

                              输入：1  1       输出： 0----无法存住1，舍去 。

 当设置为1时：     输入：1  0      输出： 1       输入：1  1        输出： 0 ----未存住，舍弃

                              输入：1   1       输出： 0      输入：1   0        输出：1----未存住，舍弃

 当复位为0时：     输入：1  0        输出： 1      输入：0    0        输出：1 （锁住了1值）            

 当设置为0时：      输入：0  1       输出： 0 ----无法存住1，舍去 。

观察可知，复位为1时可以锁住0，复位为0时存住1。当同时输入0的时候只能存入上一个值。（自己好好看看，算算输入和输出！！！）

这只存了一位，八个或特定个数组合在一起的叫做寄存器，所能存放数字的位数叫做位宽。

放入数据的动作叫写入，拿出叫做读取。

如上文，如果用设置和复位两天线可能会有些难以理解。所以我们把复位和设置收起来，延申出一条输入线（输入要存的数字）和一条允许写入线（表示是否要存取数字）。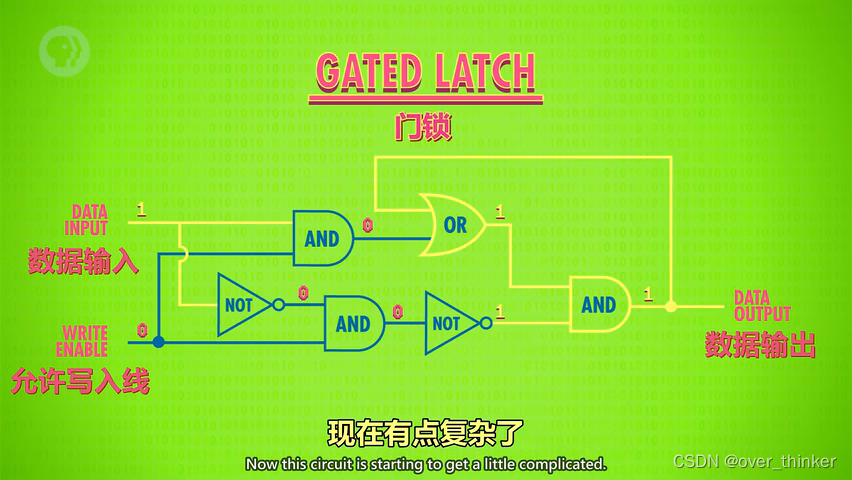

 是不是有些复杂了呢？让我们抽象一下。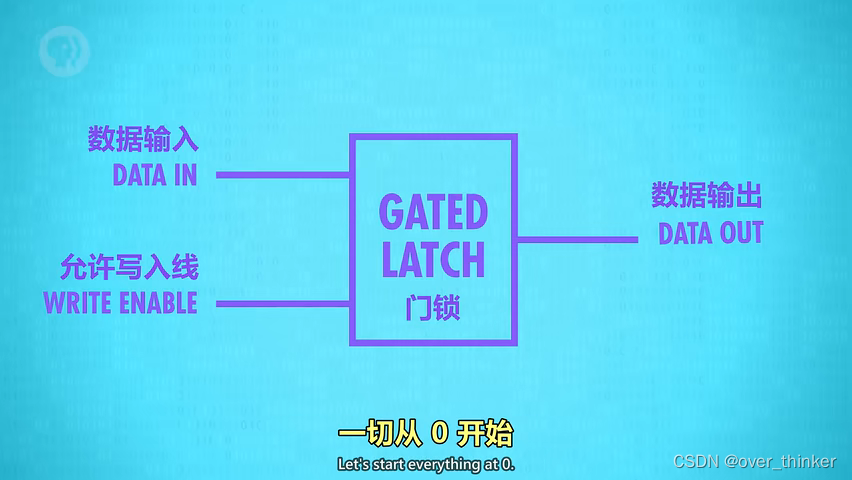

 现在的输入情况就是：

                    数据输入      允许写入                  数据输出

1）               1                       0                                 0    

2）               0                       0                                 0

3）               1                      1                                  1

4）               1                       0                                 1

5）               0                       1                                 0

观察到了了吗？只有允许写入线是开的，值才能被存进去，当他关上时，无论值怎么变化，输出都不会变---就像一个门锁。

这是存一位，那么存八位，就用八位的锁存器。这样一组的锁存器叫做寄存器，寄存器能存的位数就做位宽。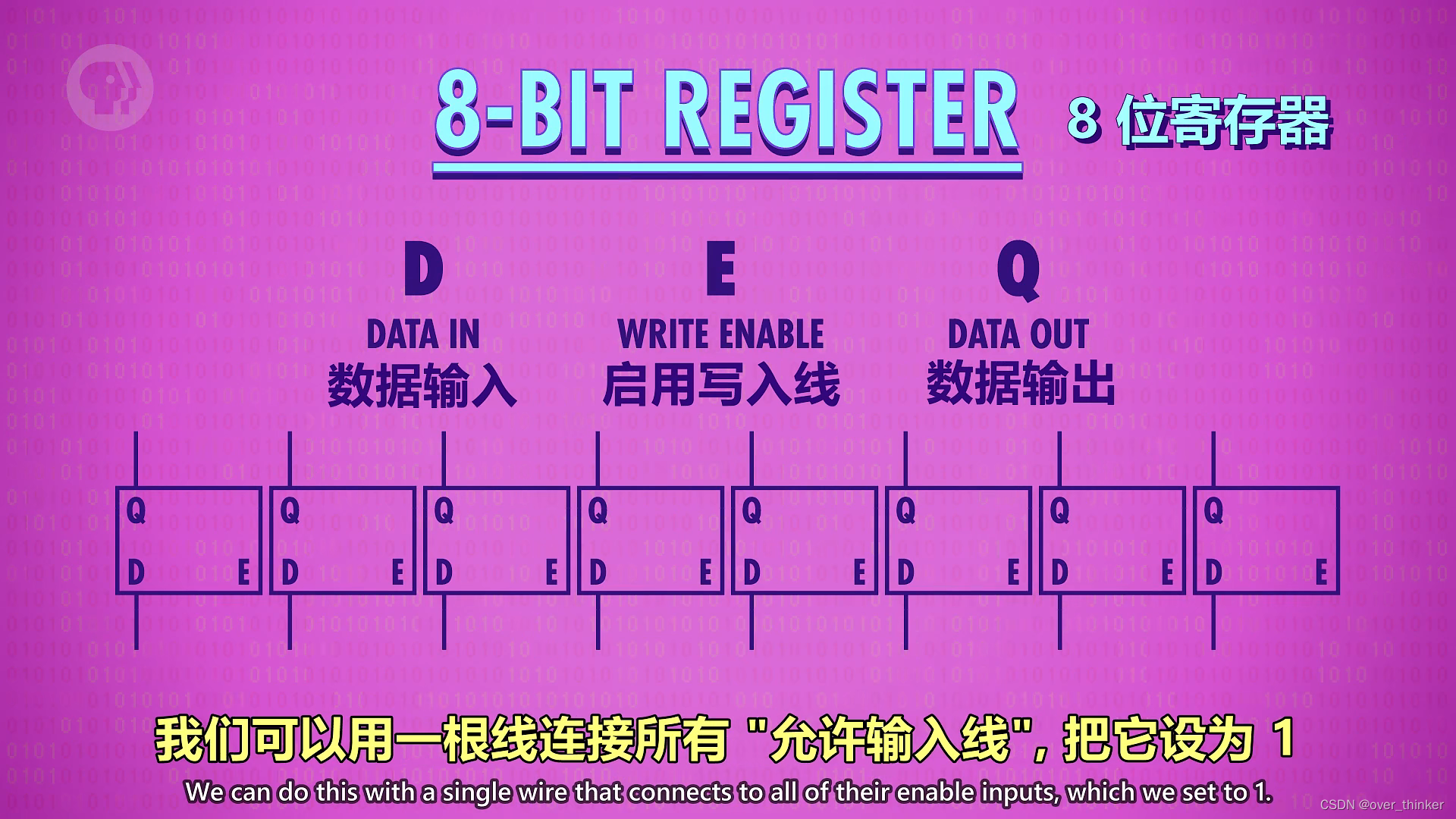

 八位寄存器可以只用一根线连接所有的允许写入线,像这样.

但显然电脑要存的不止8位而是32位,64位.

所以我们使用了矩阵.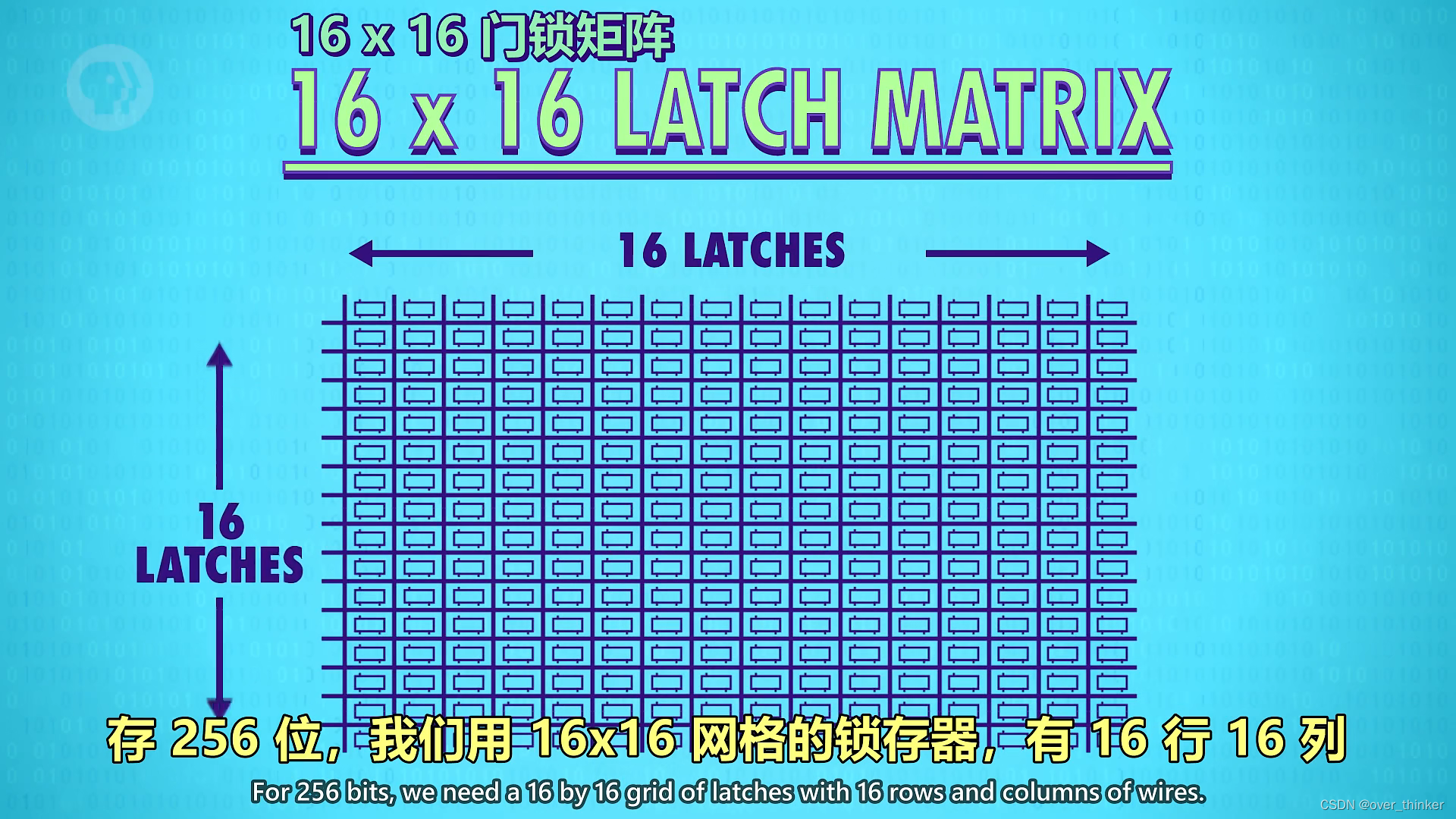

 此时行列线需要都为1时才允许写入.线的数量也大大减少,16+16+1(数据线)+1(允许写入线)=35

此时需要具体的行列号,我们就有了地址的概念.

例如12行8列就是:1100 1000,我们利用多路复用器来处理.

 利用这个找到具体的行列号,确定位置,是不是觉得有些复杂呢?那我们就再抽象一次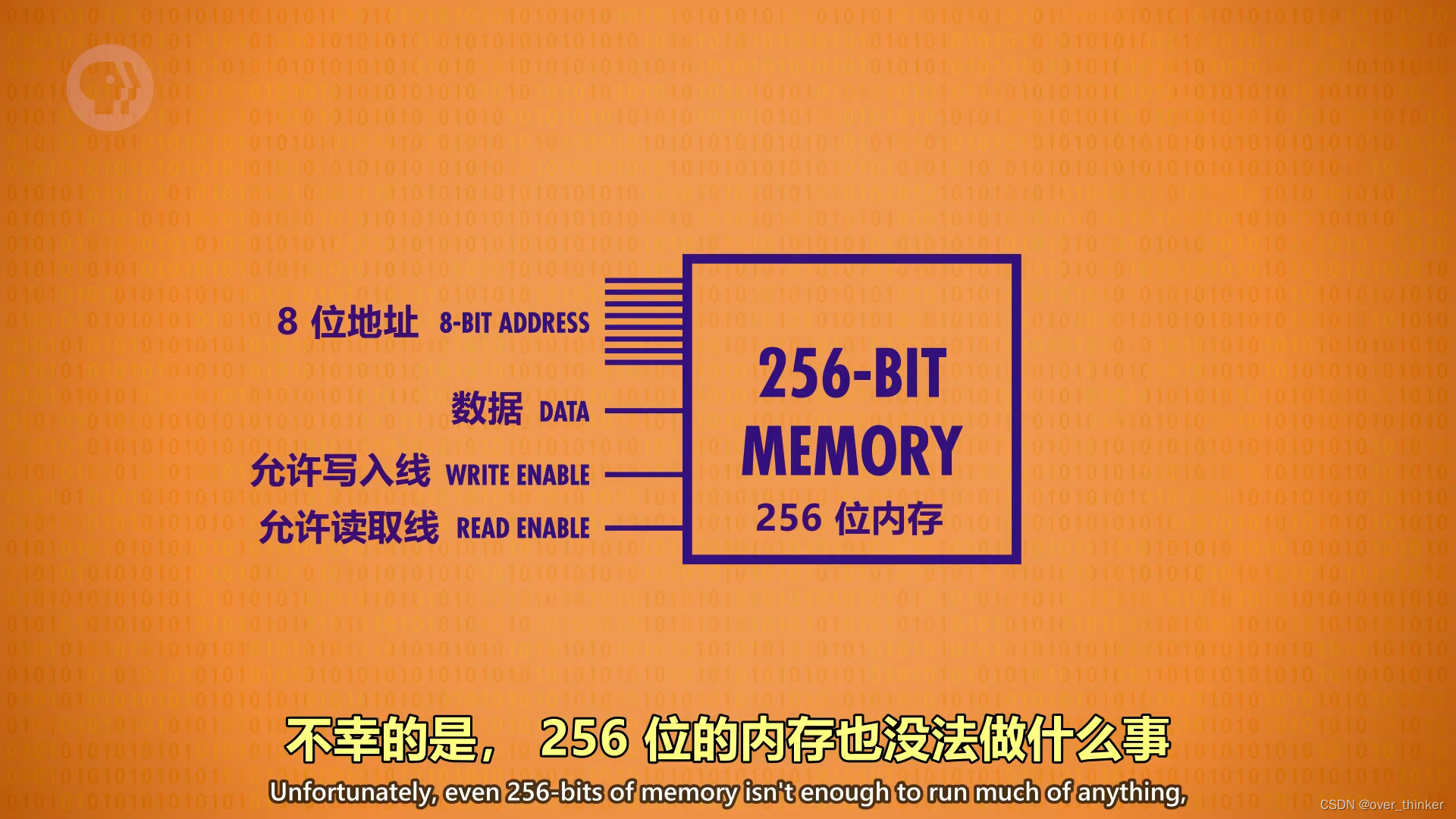

 这是一个能存256位的内存,可惜的是只是从0~256这也做不了什么事,我们需要更多更大的内存空间,像这样.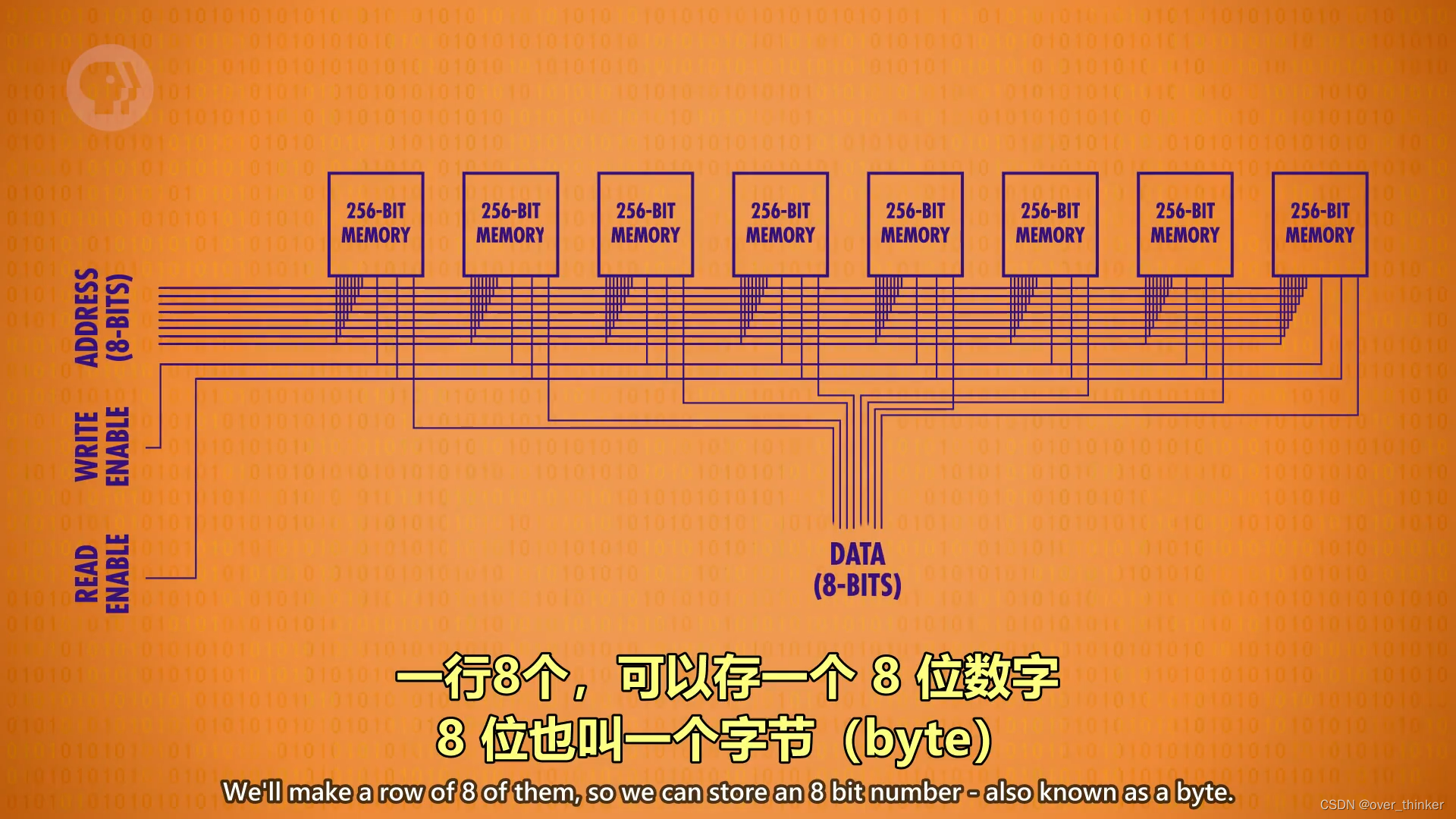

像这样,一个存一位,八个即有八位.这样我们就存了256个八位的数字,有256个地址.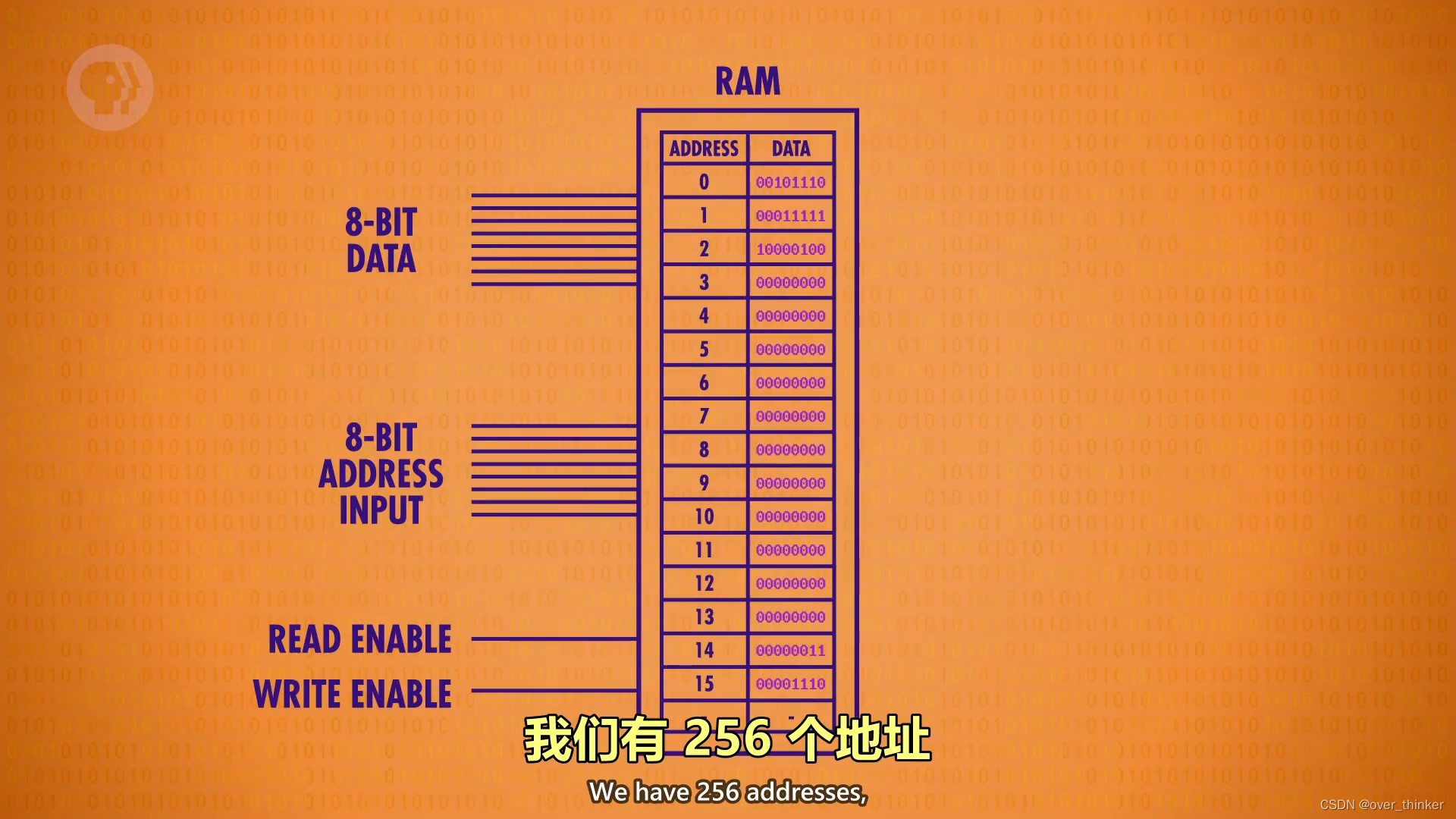 

这又是一个内存,,是一个不顾及电路,存储方式的内存--想起来了吗?栈区.

但就是这样表达的位数也不多,最大也只有255.

这就是RAM,随时访问任何位置. 

CPU