leetcode 4. Median of Two Sorted Arrays（二分查找）

最新推荐文章于 2023-06-12 16:30:30 发布

原创最新推荐文章于 2023-06-12 16:30:30 发布 · 270 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

85 篇文章

订阅专栏

本文介绍了一种在O(log(m+n))时间内找到两个有序数组中位数的算法，通过二分查找和分割点策略，实现了高效计算。文章详细解释了算法思路和实现过程，包括如何确定分割点以及如何确保分割后的左右部分满足中位数计算条件。

题目描述：

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

思路：

1.新建一个长度为m+n的数组，遍历两个数组，利用归并的方法将它们排好序放到新数组中，并返回对应新数组的中位数。

时间复杂度o(m+n)，空间复杂度o(m+n).

2.题目中要求时间复杂度为o(logn)，首先想到二分查找。

本题也可以参考数据流中的中位数https://blog.youkuaiyun.com/orangefly0214/article/details/87926398，如果我们能够将从一个数组中获得左边最大，右边最小，则很容易求得中位数。

注：将m个元素分割，会有m+1个分割点，idx分别为0-m,数组分割的情况：

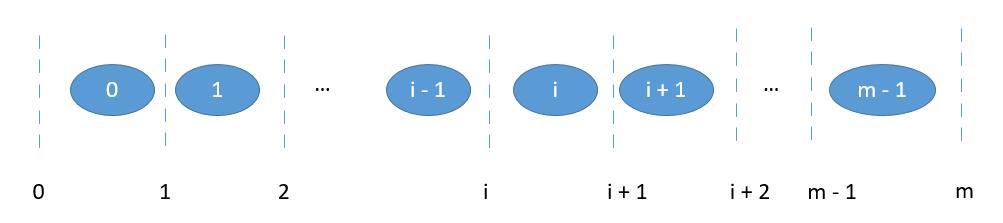
若我们的数组为A，B两个数组，对它们进行如下构造：

（1）将数组A从第i个元素处分割，因为A有m个元素，所以会有m+1个分割点，它们的id记为0-m

（2）将数组B从第j个元素处进行分割，B有n个元素，所以会有n+1个分隔点，id记为0-n

（3）将A，B放到一起，左边在一个集合，右边在同一个集合，分别用left_part和right_part表示：

假设：左右两边长度相等，且左边最大值小于右边最小值。

1) len(left_part) == len(right_part)
2) max(left_part) <= min(right_part)

这样的话我们就将数组集合分成了两部分，且左边最大值小于右边最小值，此时我们就可以获得中位数：

median = (max(left_part) + min(right_part))/2.

根据上图，两个数组我们分别以i,j为分割点，且左右两边相等，则很容易得到：

①i+j=m-i+n-j（或者i+j=m-i+n-j+1）

假定n>m,那么i的变化范围就是0-m,由上面等式得j=(m+n+1)/2-i

②同时我们要保证

B[j-1] <= A[i] and A[i-1] <= B[j]

实现：

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m=nums1.length;
        int n=nums2.length;
        if(m>n){
            return findMedianSortedArrays(nums2,nums1);
        }
        int start1=0;//start1和end1表示切割线的起止点,m个元素会有m条切割线
        int end1=m;
        int c=(m+n+1)/2;
        while(start1<=end1){
            int split1=(start1+end1)/2;
            int split2=c-split1;
            if(split1<m&&nums2[split2-1]>nums1[split1]){
                start1=split1+1;//split1太小，需要右移
            }else if(split1>0&&nums1[split1-1]>nums2[split2]){
                end1=split1-1;//split1太大，需要左移
            }else{
                int mLeft=0;
                int mRight=0;
                //分割点刚好合适
                if(split1==0){
                    mLeft=nums2[split2-1];
                }else if(split2==0){
                    mLeft=nums1[split1-1];
                }else{
                    mLeft=Math.max(nums1[split1-1],nums2[split2-1]);
                }
                if((m+n)%2==1){
                    return mLeft;
                }
                if(split1==m){
                    mRight=nums2[split2];
                }else if(split2==n){
                    mRight=nums1[split1];
                }else{
                    mRight=Math.min(nums1[split1],nums2[split2]);
                }
                return (mLeft+mRight)/2.0;
            }
        }
        
        return 0.0;
    }
}

参考：

https://leetcode.com/problems/median-of-two-sorted-arrays/discuss/2481/Share-my-O(log(min(mn)))-solution-with-explanation

https://windliang.cc/2018/07/18/leetCode-4-Median-of-Two-Sorted-Arrays/