二叉树链式存储及二叉树各种遍历的算法实现

二叉树链式存储及二叉树各种遍历的算法实现

书是一种一对多的逻辑结构，在使用链式存储的时候，经常使用的是二叉链表（三个域：左孩子指针域，数据域，右孩子指针域），三叉链表（左孩子域，数据域，双亲域，右孩子域），这里使用的是二叉链表完成了几个最基本的二叉树的操作。

#include <iostream>
using namespace std;


typedef struct BiTNode
{
	char data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//1.创建树
struct BiTNode* CreateBiTree(char data)
{
	struct BiTNode* T = (struct BiTNode*)malloc(sizeof(struct BiTNode));
	T->data = data;
	T->lchild = NULL;
	T->rchild = NULL;
	return T;
}
void insertNode(struct BiTNode* curNode, struct BiTNode* lefNode, struct BiTNode* rigNode)
{
	curNode->lchild = lefNode;
	curNode->rchild = rigNode;
}

void printData(struct BiTNode* curNode)
{
	cout << curNode->data;
}

void preorder(struct BiTNode* tree) //递归前序
{
	if (tree != NULL)
	{
		printData(tree);
		preorder(tree->lchild);
		preorder(tree->rchild);

	}
}

void midorder(struct BiTNode* tree) //递归中序
{
	if (tree != NULL)
	{
		midorder(tree->lchild);
		printData(tree);
		midorder(tree->rchild);

	}
}

void postorder(struct BiTNode* tree)  //递归后序
{
	if (tree != NULL)
	{
		postorder(tree->lchild);
		postorder(tree->rchild);
		printData(tree);
	}
}

void midorderbystack(struct BiTNode* tree)   //非递归中序遍历
{
	if (tree == NULL)
		return;
	struct BiTNode* stack[10];
	int stacktop = -1;
	struct BiTNode* pmove = tree;
	while (stacktop != -1 || pmove)
	{
		while (pmove)
		{
			stack[++stacktop] = pmove;
			pmove = pmove->lchild;
		}
		if (stacktop != -1)
		{
			pmove = stack[stacktop--];
			cout << pmove->data;
			pmove = pmove->rchild;
		}
	}
}

void preorderbystack(struct BiTNode* tree)   //非递归前序遍历
{
	if (tree == NULL)
		return;
	struct BiTNode* stack[10];
	int stacktop = -1;
	struct BiTNode* pmove = tree;
	stack[++stacktop] = pmove;
	while (stacktop != -1)
	{
		pmove = stack[stacktop--];
		cout << pmove->data;
		if (pmove->rchild != NULL)
			stack[++stacktop] = pmove->rchild;
		if (pmove->lchild != NULL)
			stack[++stacktop] = pmove->lchild;
	}
}

void postorderbystack(struct BiTNode* tree)   //非递归后序遍历
{
	if (tree == NULL)
		return;
	struct BiTNode* stack[10];
	int stacktop = -1;
	struct BiTNode* p = tree; //移动节点
	struct BiTNode* q = NULL; //标记结点
	while (p != NULL)
	{
		while (p->lchild != NULL)
		{
			stack[++stacktop] = p;
			p = p->lchild;
		}
		while (p != NULL && (p->rchild == NULL || p->rchild == q))
		{
			cout << p->data;
			q = p;
			if (stacktop == -1)
			{
				return;
			}
			p = stack[stacktop--];
		}
		stack[++stacktop] = p;
		p = p->rchild;
	}

}

void levelorderbyqueue(struct BiTNode* tree)
{
	if (tree == NULL)
	{
		return;
	}
	struct BiTNode* queue[10];
	int front, rear;
	front = rear = 0;
	struct BiTNode* p = tree;
	rear = (rear + 1) % 10;
	queue[rear] = p;
	while (front != rear)
	{
		front = (front + 1) % 10;
		p = queue[front];
		cout << p->data;
		if (p->lchild != NULL){ rear = (rear + 1) % 10; queue[rear] = p->lchild; }
		if (p->rchild != NULL){ rear = (rear + 1) % 10; queue[rear] = p->rchild; }
	}
}


void main()
{
	struct BiTNode* A = CreateBiTree('A');
	struct BiTNode* B = CreateBiTree('B');
	struct BiTNode* C = CreateBiTree('C');
	struct BiTNode* D = CreateBiTree('D');
	struct BiTNode* E = CreateBiTree('E');
	struct BiTNode* F = CreateBiTree('F');
	struct BiTNode* G = CreateBiTree('G');

	insertNode(A, B, C);
	insertNode(B, D, E);
	insertNode(D, F, NULL);
	insertNode(E, NULL, G);

	cout << "递归先序遍历："; preorder(A); cout << "\n";
	cout << "递归中序遍历："; midorder(A); cout << "\n";
	cout << "递归后序遍历："; postorder(A); cout << "\n";
	cout << "非递归先序遍历："; preorderbystack(A); cout << "\n";
	cout << "非递归中序遍历："; midorderbystack(A); cout << "\n";
	cout << "非递归后序遍历："; postorderbystack(A); cout << "\n";
	cout << "层次遍历："; levelorderbyqueue(A); cout << "\n";
	system("pause");
}

二叉树如下：

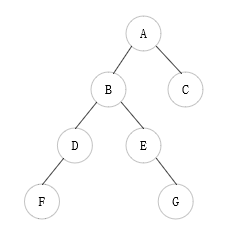
简单讲一下二叉树非递归的三种遍历方法：
1.非递归先序遍历：非递归先序遍历使用的是栈结构来实现的。大致思路是，首先将根节点入栈，只要栈不为空就出栈一个元素，然后将这个元素的右孩子和左孩子分别入栈，重复以上操作，知道栈中元素为空时，结束遍历。

2.非递归中序遍历：非递归中序遍历的方法也是栈结构来实现的。大致思路是，创建一个移动的结构体指针，如果结点不为空，则入栈，然后结构体指针指向自己的左孩子（p = p -> lchild），直到p为空为止，这时候 判断栈是否为空，如果不为空，则出栈一个元素，p指向这个出栈元素，输出这个元素，移动的结构体指针p在指向这个元素的右孩子(p = p -> rchild)，重复这部分操作，直到栈中元素为空时，结束。

3.非递归后序遍历：非递归中序遍历的方法也是栈结构来实现的。大致思路是，创建一个移动的结构体指针 p 和一个用来做标记的结构体指针 q ，首先将根节点入栈，然后将根节点的左孩子入栈，只要入栈结点的左孩子不为空时，则将元素一直入栈，当入栈元素的左孩子为空时，这时候判断 p 指向的元素的右孩子是否为空或者是否指向标记的指针，如果这个条件不满足（有右孩子），则将这个结点入栈，移动的结构体指针指向入栈元素的右孩子（p = p -> rchild），这时候重复上面的过程，当满足入栈元素的右孩子是否为空或者是否指向标记的指针时，这时候打印这个元素 p 指向的元素，然后让 q = p; 标记这个元素结点被标记（已经被遍历过了），然后出现一个元素让 p 指向这个出栈的元素。重复上述过程，当栈为空是，遍历结束。

4.层次遍历：层次遍历二叉树的方法使用队列来实现的。大致思路是，首先将根节点入队，如多队列不为空就出队一个元素，再将这个出队元素的左右孩子分别入队，重复上述步骤，如果队列为空，则层次遍历结束。

二叉树的非递归遍历需要好好理解，大家可以看我上面写的大致思路，参考代码来领悟。有不解得可以发评论或者私信。