二叉树之存储结构及遍历算法【数据结构】

二叉树存储结构

二叉树的顺序存储

按结点层次编号，依次存放。
特点：结点间关系蕴含在其存储位置中。
浪费空间，适合存满二叉树和完全二叉树。

案例

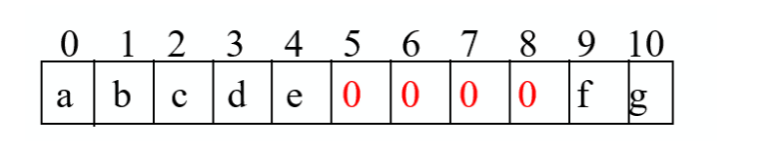
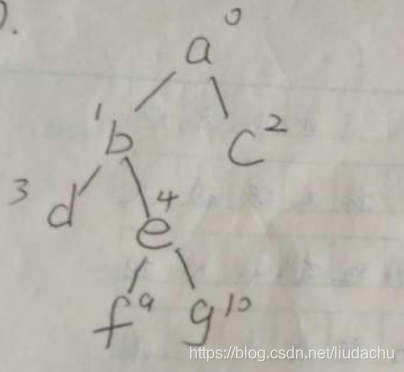
对应的二叉树

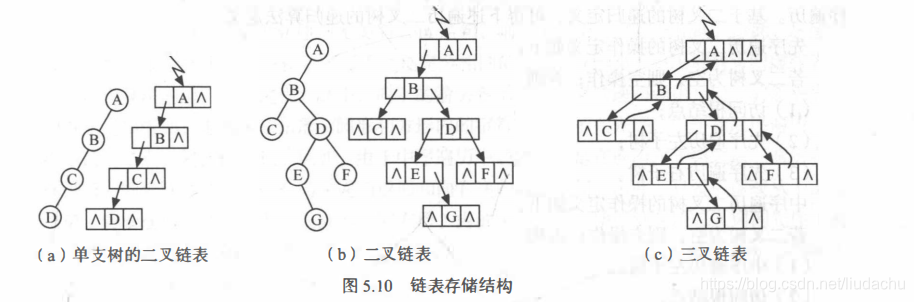
二叉树的链式存储

定义结点类型：
  typedef struct BiNode{
     TElemType data;
     struct BiNode *lchild,*rchild;//左右孩子的指针
  }BiNode,*BiTree;
  三叉链表结点指针类型：
  typedef struct TriTNode{
      TelemType data;
       struct TriTNode *lchild,*parents,*rchild;
  }
  

遍历算法

遍历：是树结构插入删除修改和排序算法的前提。
先序遍历：先根再左再右
中序遍历：先左再根再右
后序遍历，先左再右再根

递归遍历算法

 1.先序遍历算法：
    Status PreOrderTraverse(BiTree T){
       if(T=NULL)return OK;//空二叉树
       else{
          输出T->data;//访问根节点
          PreOrderTraverse(T->lchild);//递归遍历左子树
          PreOrderTraverse(T->rchid);//递归遍历右子树
       }
    } 
   2. 中序遍历算法：
    Status InOrderTraverse(BiTree T){
      if(T=NULL)return OK;
      else{
        InOrderTraverse(T->lchid);//递归遍历左子树
        输出T->data;//访问根结点
        InOrderTraverse(T->rchid);//递归遍历右子树
      }
    }
    3.后序遍历算法：
    Status InOrderTraverse(BiTree T){
      if(T=NULL)return OK;
      else{
        InOrderTraverse(T->lchid);//递归遍历左子树        
        InOrderTraverse(T->rchid);//递归遍历右子树
        输出T->data;//访问根结点
      }
    }

非递归算法

****中序遍历的非递归算法：
****算法核心----指针不空进栈并指向左子树，为空出栈输出并指向右节点

    void InOderTraverse(BiTree T){
        InitStack(S);//初始化栈
        P=T;//指向根节点
        q=new BiNode;//用来接收退栈的节点
        while(p||!StackEmpty(S)){//当p为空并且栈为空时退出循环
            if(p){                     //p非空
               Push(S,p);//根节点进栈
               p=p->lchild;//指向左节点
            }
            else                      //p空
            {
                Pop(S,q);//出栈
                count<<  q->data;//输出出栈的元素
                p=q->rchild;//指向右节点。
            }
            
        }
    }
    方式二、
    void InOderPraverse(BiTree T){
        InitStack(S);//初始化栈
        Push(S，T);//根节点入栈
        while(!StackEmtpy(S)){//栈为空退出循环
          while(GetTop(S,p)&p)
             Push(S,p->lchild);   //循环入栈直到没有左子树  
          Pop(S,p)//空指针退栈
          if(!StackEmpty(S))Pop(S,p);//出栈
          conut<<(p->data);//输出
          Push(S,p->rchild);;/根节点输出后，指向右子树          
        }
    }

二叉树遍历算法的应用案例

案例树

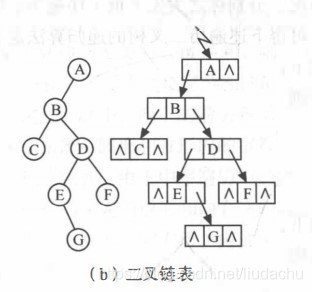
代码

#include<stdio.h>
#include <stdlib.h>
typedef int Status; 
//定义结点类型
typedef struct BiNode{
	char data;//数据域
	struct BiNode *lchild,*rchild;//左指针，右指针 
}BiNode; 
typedef BiNode* BiTree;//定义二叉树类型 
typedef BiTree ElemType;//定义数据类型
//创建二叉链表表示的二叉树(按先序次序输入) 
Status CreatBiTree(BiTree &T)
{
	char ch;
	ch=getchar();
	if(ch=='#')T=NULL;
	else{
		T=new BiNode;T->data=ch;//新结点赋值
		CreatBiTree(T->lchild);//左节点遍历创建子树 
		CreatBiTree(T->rchild); //右节点遍历创建子树 
	}
}
//定义链栈结点
typedef struct StackNode{
	ElemType data;
	struct StackNode *next; 
}StackNode;
//定义链栈链表
typedef StackNode* LinkStack;
//初始化链栈 
Status InitStack(LinkStack &S)
{
	S=NULL;	
}
//链栈进栈 
Status Push(LinkStack &S,ElemType e)
{
	LinkStack p;//新结点 
	p=new StackNode;
	if(!p)return 0;
	p->data=e;
	p->next=S; 
	S=p;
	return 1;	
}
//链栈出栈 
Status Pop(LinkStack &S,ElemType &e)
{
	LinkStack p=S;
	e=p->data;
	S=S->next;
	delete p;
	return 1;	
}
bool StackEmpty(LinkStack S){//判断栈是否为空 
	if(!S)return true;//栈空
	return false;	
}  
//中序非递归遍历算法
Status InorderTraverse(BiTree T){
	LinkStack S;
	InitStack(S);
	BiTree p=T;//指向根结点 
	BiTree q; //用来接收退栈的结点 
	while(p||!StackEmpty(S))//当p为空并且栈为空时退出循环
	{
		if(p){//p非空 
			Push(S,p);//根节点进栈 
			p=p->lchild;//指向左节点 
		}
		else
		{
			Pop(S,q);//出栈
			printf("%c",q->data);
			p=q->rchild;//指向右节点 
		} 
	}
}
//中序遍历递归算法
Status InOrderTraverse(BiTree T)
{
	if(T)
	{
		InOrderTraverse(T->lchild);
		printf("%c",T->data);
		InOrderTraverse(T->rchild);
	}
}
//前序遍历递归算法
Status PreOrderTraverse(BiTree T)
{
	if(T)
	{
		printf("%c",T->data);
		PreOrderTraverse(T->lchild);		
		PreOrderTraverse(T->rchild);
	}
}
//后序遍历递归算法
Status WOrderTraverse(BiTree T)
{
	if(T)
	{
		WOrderTraverse(T->lchild);	
		WOrderTraverse(T->rchild);
		printf("%c",T->data);
	}
}
//计算结点个数
int NodeCount(BiTree T){
	if(T==NULL)return 0;
	else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
} 
//计算二叉树深度
int Depth(BiTree T){
	if(T==NULL)return 0;
	int d1=Depth(T->lchild);
	int d2=Depth(T->rchild);
	if(d1>d2)
	return d1+1;
	return d2+1;
}
//计算叶子结点的个数
int CountLeaf(BiTree T){
	if(T==NULL)return 0;
	if(T->lchild == NULL && T->rchild == NULL)return 1;
	return CountLeaf(T->lchild) + CountLeaf(T->rchild);
} 
int main(){
	BiTree bt;
	CreatBiTree(bt);//ABC##DE#G##F###
	if(bt)printf("创建成功\n");
	printf("前序遍历的结果:");
	PreOrderTraverse(bt);
	printf("中序遍历的结果:");
	InOrderTraverse(bt);
	printf("后序遍历的结果:");
	WOrderTraverse(bt);
	printf("\n二叉树结点个数：%d个",NodeCount(bt));
	printf("\n二叉树的深度为：%d",Depth(bt));
	printf("\n二叉树的叶子结点个数：%d个",CountLeaf(bt));
}