基于吠陀乘法器的低功耗滤波器设计

原创于 2025-10-20 10:26:32 发布 · 623 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#吠陀乘法器 #低功耗 #自适应滤波器 #LMS算法 #FIR滤波器

AI助手已提取文章相关产品：

基于吠陀乘法器的低功耗自适应滤波器设计

摘要

本文探讨了一种使用吠陀乘法器（VM）设计自适应滤波器（AF）的架构方法，该方法在不改变滤波器性能的前提下有效降低功耗，称为基于吠陀乘法器的低功耗自适应滤波器（LPAFVM）。AF包含一个可变滤波器（VF）和一个用于更新滤波器系数的算法。通常，滤波器在影响自适应系统功耗方面起着主要作用；通过根据滤波器系数和输入数据的幅度消除不必要的乘法运算，可以显著降低功耗。VM能够在较少的步骤内完成乘法运算。LMSA—最小均方算法用于设计FIR滤波器。自适应过程通过将可变滤波器计算出的输出与LMS算法的期望输出进行收敛来实现。采用Xilinx ISE 14.6对所提出的架构进行仿真和综合。功耗通过Xilinx ISE套件中的Xpower分析器进行计算。

关键词

可重构设计 Low功耗滤波器 LMS algorithm 自适应滤波 Vedic乘法器

1 引言

数字信号处理器（DSP）系统的主要目标是可视化、分析和转换包含信息的模拟信号，将其转化为可用于实时场景的有效信号形式。如今，数字信号处理领域正在发生许多技术进步，例如回声消除、噪声消除、语音预测等 [1–7]。人们始终期待获得可接受且快速地解决这些问题。因此，相比标准的数字信号处理技术，采用了自适应滤波技术。无论如何，滤波是数字信号处理中最广泛使用的操作。滤波器用于从噪声信号中提取期望信号，而自适应滤波器是一种包含具有可变参数控制的传递函数的线性滤波器系统，并配备一种优化算法来相应地调整这些参数。滤波和自适应是自适应滤波器运行中的两个过程。FIR滤波器用于常规滤波操作，而该滤波器需要乘法器。用吠陀乘法器替代标准乘法器，可以减少计算步骤并提高运算速度。自适应算法用于自动更新滤波器系数。整个系统的性能和功耗在很大程度上取决于滤波器的功能。因此，低功耗滤波器的设计已成为一个重要课题。所提出的LPAFVM架构由于采用自适应滤波器和吠陀乘法器实现，具有较高的运算速度和较低的功耗。

2 吠陀乘法器的介绍与框图

在20世纪早期，古印度数学体系被重新发现，它基于16条苏特拉（原理或文字公式）。这些苏特拉为数字信号处理（DSP）领域带来了新的启示，例如可以利用吠陀乘法算法实现数字乘法器。吠陀乘法器架构（VM architecture）采用乌尔杜瓦·特里延卡比延姆苏特拉（垂直交叉法）实现。古代印度曾使用该苏特拉快速完成两个十进制数的乘法运算。同样的概念被应用于二进制数（基数2）系统，从而简化了数字硬件的设计。

示意图0

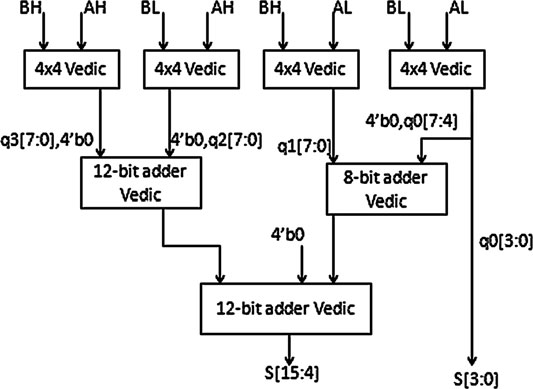
VM算法

取两个8位数字。例如：a = a7a6a5a4a3a2a1a0 和 b = b7b6b5b4b3b2b1b0。
将两个8位数字各分成两部分，每部分包含两个4位数字。例如：{AL = a3a2a1a0, AH = a7a6a5a4, BL = b3b2b1b0, BH = b7b6b5b4}。
按照电路结构，将这四个部分作为输入分配给四个4 × 4乘法器模块。a3a2a1a0 和 b3b2b1b0 作为第一个4 × 4乘法器的输入；a3a2a1a0 和 b7b6b5b4 作为第二个4 × 4乘法器的输入；a7a6a5a4 和 b3b2b1b0 作为第三个4 × 4乘法器的输入；a7a6a5a4 和 b7b6b5b4 作为第四个4 × 4乘法器的输入。
从第一个4 × 4乘法器的输出中，将低4位（LSB bits）分配给最终结果的最低有效位。
将第二个乘法器的输出与第一个乘法器输出的剩余位（在高位补四个零以形成一个8位数）作为8位加法器的输入。即：{q1[7:0], {00, q0[7:4]}}。
第三和第四乘法器的输出均为8位，我们在第三乘法器的输出前补四个零作为最高有效位（MSB），在第四乘法器的输出后补四个零作为最低有效位（LSB）。
这两个值作为第一个12位加法器的输入。即：{{q3[7:0], 0000}, {0000, q2[7:0]}}。
现在，第一个12位加法器的输出和8位加法器的输出作为第二个12位加法器的输入。即：{12位和值, {0000, 8位和值}}。将第二个12位加法器的和值以及第一个4 × 4乘法器的4个最低有效位分配给最终结果。即：{12位加法器的和值, q0[3:0]}。

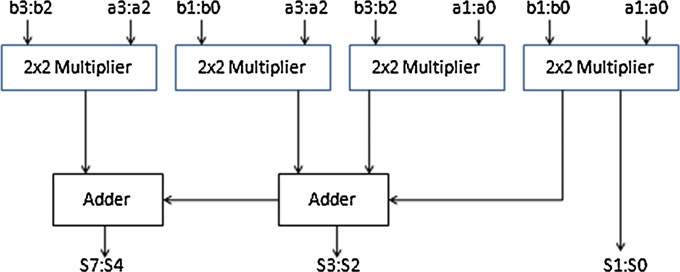
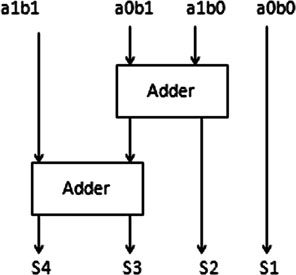
设计8 × 8位VM需要4 × 4 VM和4 × 4位VM需要2 × 2位VM。在此上下文中，2 × 2位VM、4 × 4VM和8 × 8VM的框图如下图所示。基本乘法器无论如何都需要简单的加法器，如半加器和全加器（图1、2、3）。

示意图1

示意图2

3 自适应滤波器的架构

自适应滤波器的架构具有自动调节特性，这是数字fi滤波器的一种属性。fi滤波器的脉冲响应被调整，以消除输入中的相关信号。有时该fi滤波器不需要关于信号和噪声特性的先验知识，但需要相关信号的期望响应。在非平稳条件下，自适应滤波器具备信号跟踪能力。自适应滤波器的框图如图4所示。

示意图3

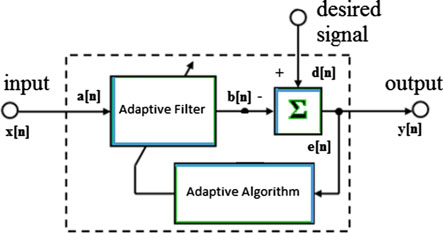
自适应滤波器包含三个基本模块：基本滤波器、性能验证器和自适应算法。滤波器结构规定了从输入样本到输出的量。由于稳定性也是一个衡量因素，因此优先选择FIR滤波器而非IIR滤波器。其次，性能验证器根据应用需求进行选择。性能验证的方法有三种：（1）最小均方，（2）平方误差和（3）加权最小二乘。性能验证器驱动自适应算法以提高性能。该自适应算法用于自动校正滤波器系数。

低功耗自适应fi滤波器如图5所示。该fi滤波器是一种可重构FIRfi滤波器，由于采用了VM，其功耗非常低。LMS算法（LMSA）用于自适应过程。此处LMSA根据性能验证器产生的均方误差值自行更新fi滤波器系数fi，fi从而得到均方误差值。

4 可重构FIR滤波器架构

FIR滤波器是一种具有有限冲激响应的数字滤波器。FIR滤波器是最简单的滤波器，仅对当前和过去的输入进行操作，也称为非递归滤波器。时不变性和线性是FIR滤波器的两个重要特性。

从数学上讲，
$$
h(n) = 0; \quad n < n_1 \quad \text{或} \quad n > n_2
$$
其中n1和n2的范围为(−∞, ∞)，h(n)是数字滤波器的脉冲响应，n表示离散时间索引，n1和n2表示范围，为常数。

连续时间微分方程的离散时间等效形式称为差分方程。FIR数字滤波器的差分方程为
$$
y(n) = \sum_{r=0}^{n-1} b_r x(n - r)
$$
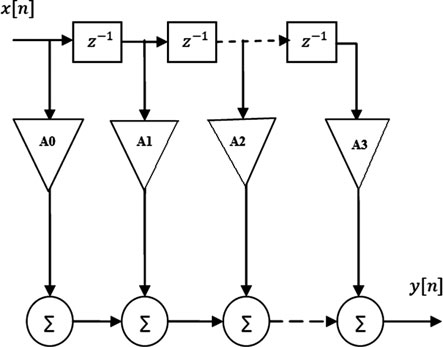
其中，不同n值对应的输出表示为y(n)，第r个前馈抽头用br表示。Σ表示从r = 0到“n − 1”的求和，x(n − r)表示滤波器延迟r个样本后的输入，n为前馈抽头的数量。由于滤波器输出是有限的，因为若仅有单个脉冲存在时，其输出即为有限输入，然后在有限时间内输出零。FIR滤波器系数的数量表示FIR滤波器输出变为几乎为零所需的时长。FIR滤波器也可称为非递归滤波器，因为其滤波器行为仅由过去和当前输入决定。

所提出的FIR filter结构消除了不必要的乘法。通过考虑filter系数和数据样本的幅度，FIR filter的阶数可以动态改变。性能由量化误差描述，该误差通过数据样本与filter系数相乘得到，其值非常小（图6）。

示意图4

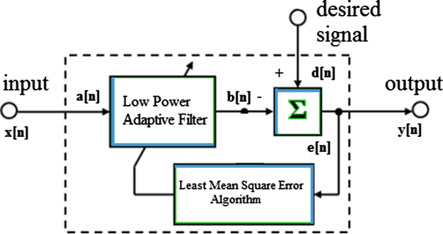
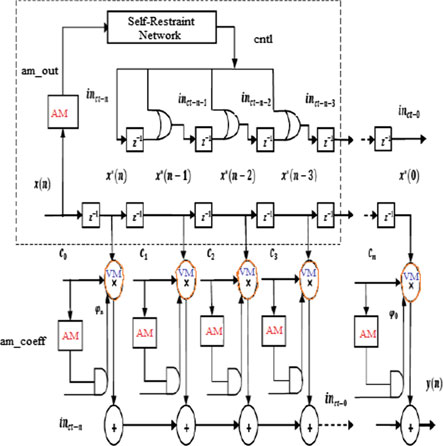
图7表示可重构的低功耗FIR滤波器。它包含三个模块：幅度监测器 (AM)、乘法器控制决策窗口(MCDW)和自约束网络(SRN)。通过消除不必要的乘法运算，该方法降低了功耗。具体而言，由于开关活动与动态功耗成正比，因此可以降低动态功耗。SRN生成所需的控制信号。

根据滤波器系数和数据样本的幅度，乘法器会自动关闭，从而节省功耗。因此，所述可重构低功耗架构能够动态更新。如果滤波器系数与数据样本乘积的幅度小于某个预设值（称为阈值），则对应的乘法器将被关闭。当输入信号的数据样本幅度小于阈值（xth）时，输出变为逻辑1。使用该方法存在问题：当数据样本在每个时钟周期快速变化时，会导致乘法器持续切换，从而增加动态功耗。为了减少这种开关活动，采用了MCDW。其中，为每个滤波器使用AM来稳定滤波器系数的幅度。AM将每个滤波器系数与数据样本的幅度相对于预设阈值（cth）的值。如果该值非常小，则输出（am_coeff）变为逻辑1。MCDW用于监测开关活动并降低发生频率。自阻网络通过生成控制信号来实现此功能。

自阻网络内部包含一个计数器，在条件[n] < xth满足之前，该计数器持续统计输入端的样本数量。当幅度监测器（am_out）输出为逻辑1时，计数器每次递增1。当计数值即MCDW大小达到某一值m时，自阻网络被置为逻辑1。因此，控制信号出现逻辑1表示已监测到m个较小的输入，此时乘法器准备关闭。

附加信号 inct−n 由信号 ctrl 控制。该附加信号伴随输入数据，用于指示 [n] < xth。当滤波器系数幅度小于 cth 时，乘法运算被取消，因此在第一抽头前增加一个延迟元件，以同步信号 inct−n 和 x*(n)。当输入端的数据样本幅度和滤波器系数幅度均小于阈值时，信号 βn 被置为逻辑1，乘法器关闭，强制输出为零。阈值 (xth, cth) 的取值确保功耗和滤波器性能无影响。如果阈值过大，虽然会降低功耗，但会导致滤波器性能下降，从而在两者之间形成权衡。

示意图5

5 自适应算法

基本的自适应滤波器如图4所示，工作在离散时间域。X(n) 是输入信号，y(n) 是输出信号。假设自适应滤波器的输入为x[n]，自适应滤波器的输出为y[n]，期望信号（噪声分量）表示为d(n)。误差信号可表示为e(n) = d(n) − y(n)。自适应算法用于根据性能准则，利用误差信号来更新滤波器系数向量w(n)。通常，整个自适应过程旨在使误差信号达到最小量，从而使自适应滤波器逼近参考信号。存在多种根据其性能设计的自适应算法。

维纳‐霍夫方程是求解最优滤波器权重的一种方法，其方程如下所示：
$$
w = R^{-1}P = W_{\text{optimum}}
$$
LMS在极限情况下，维纳‐霍夫方程是对最速下降过程的一种递归使用的随机逼近。LMSA是“最速下降算法”的有噪逼近，通过沿负梯度方向进行一步迭代，实现对系数向量的自动更新。
$$
w(n + n_0) = w(n) - \frac{\lambda}{2} \frac{dJ_w}{dw(n)}
$$
其中λ表示控制收敛速度和稳定性的步长，此处n₀等于1。LMSA使用目标函数来求梯度值，该梯度由均方误差的估计值J_w = e²(n)构成，结果为δJ_w/δw(n) = −2e(n) × x(n)。

LMSA:

对于每个n的值
{
- y(n) = conv(wᵀ(n), x(n))
- 误差 = d(n) – y(n)
- w(n + n₀) = w(n) + 2λ × 误差 × x(n)
}

为了跟踪期望输出，LMSA使用误差信号(e(n))来更新滤波器系数。
滤波器的输出y(n)表示为wᵀ(n)。滤波器系数的转置形式wᵀ(n)，x(n)是输入端的滤波样本，误差信号e(n)用于更新滤波器系数，步长表示为λ，也称为学习因子。

示意图6

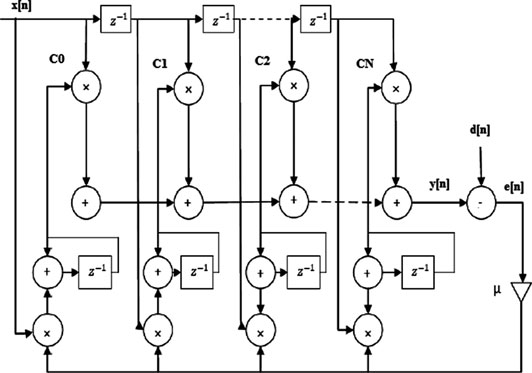
LMS自适应滤波器结构的通用直接形式如图8所示。该结构可用于更新滤波器抽头权重。更新滤波器抽头权重所需的方程为w(n + n₀) = w(n) + λe(n)x(n)。

6 仿真结果

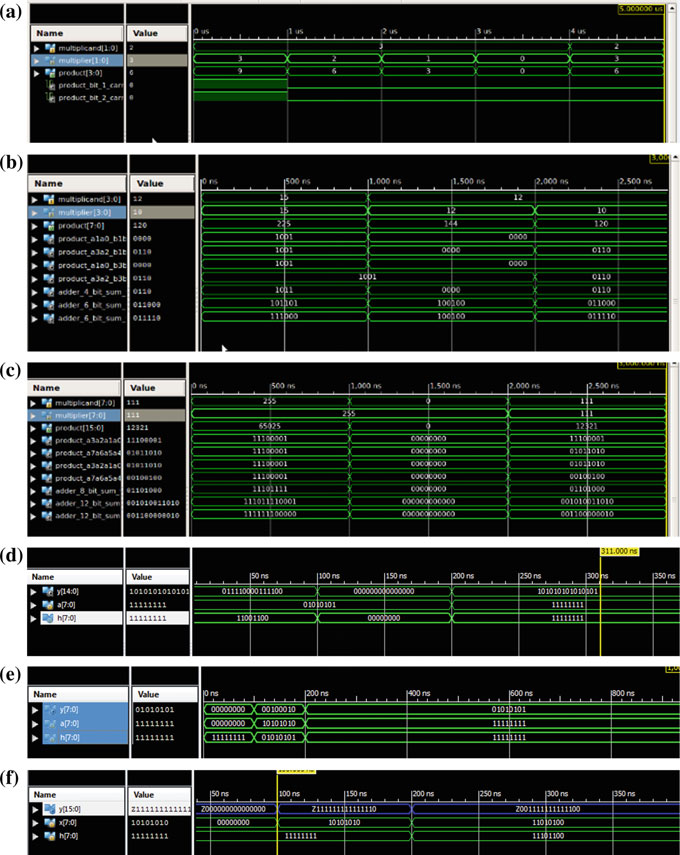
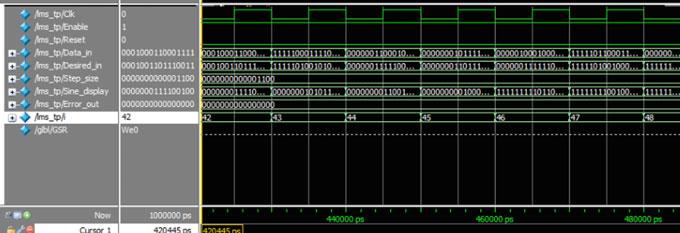
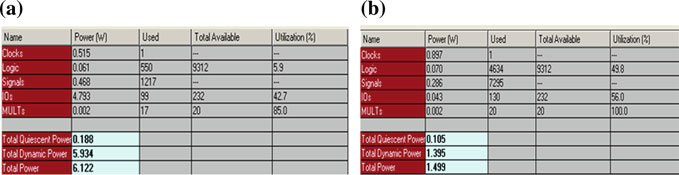
使用Verilog对吠陀乘法器和低功耗自适应滤波器进行分析，并在Xilinx ISE 14.6上进行仿真和综合。用于描述滤波器的输入数据样本和系数为16位。结果与传统FIR滤波器进行了比较。同时使用Modelsim验证了滤波器的响应，并展示了仿真结果。图9表示VM的截图，图10显示了传统FIR滤波器，图11显示了AF。使用Xilinx ISE套件中的Xpower分析进行功耗分析，如图12所示。比较图如图13所示。

示意图7