迷宫想必大家都比较熟悉,想走出一个迷宫,最重要的就是不要在同一个地方走两次,每当遇到一个路口时,将要走的路标记出来,如果没成功下次也就不用再走这边了。
迷宫有很多种,比如:一个通路,多个通路不带环,多个通路带环等,迷宫的解法通常都用回溯法。
回溯法:对于一个包括有很多的结点,每个结点有若干个搜索分支的问题,把原问题分解成为若干个子问题求解的算法;当搜索到某个结点发现无法再继续搜索下去时,就让搜索过程回退到该节点的前一个结点,继续搜索该结点外的其他尚未搜索的分支;这样的搜索过程一直进行到搜索到问题的解或者搜索完了全部可搜索分支没有解存在为止。
以一个复杂迷宫为例子:

我们规定求一个结点的周围结点的情况时,按上,左,右,下的顺序判断;
看到一个迷宫,最先得知道迷宫的入口(x=9,y=1),在走迷宫时,我们要先判断这个结点是否为通路?如果是1,那么就是通路,将其标记了(当前步的数+1),证明已经走过了,同时将坐标压栈。这步走完之后,下一步就是判断当前结点的周围结点,再判断前必须要拿到这个结点的坐标,所以拿到栈顶的元素,让栈顶的元素的x,y做相应的变化依次判断周围的结点。按照这样的规则和顺序,当我们走到(5,2)时发现这个结点的上,左,右,下已经走不通了,所以根据回溯法,回到前一个结点(5,3),同时出栈,再次按照规则和顺序,在(9,3)处我们走到了第一个出口,这时我们要保存这个路径(路径的坐标都在栈当中),保存后,我们要去寻找其他的出口,以判断那条路经的距离最短;所以,出栈,回到前一个改变方向的结点(6,3),再次按照规则和顺序,走到(5,9)我们找到第二个出口,用当前的路径和上一条路径比较,然后得到当前的最短的路径。保存再出栈,(5,4)的两条的路径已经全部判断,继续出栈,回到(5,1);
走到这时我们发现迷宫中已经再没有1了,但是(5,1)的右边结点我们并没有判断,所以我们规定在判断当前结点或者周围结点时,不仅仅是1,或者当下一个结点的数大于当前节点的数时,就视为通路。
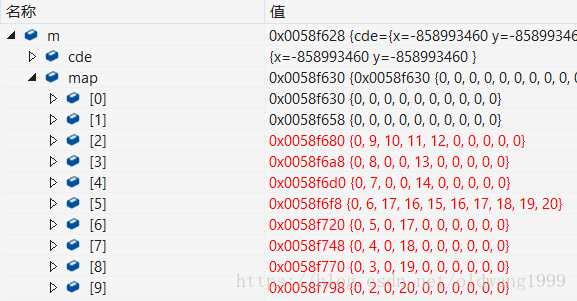
我们在(5,1)继续走迷宫,按照规则和顺序往右走(走到(5,2),17已经改为7),到(5,4)往上走,走到(0,4),发现走不通,按照规则出栈,回到(5,4),再按规则往右走,找到刚才的第二个出口为第三条路径,更新最短路径,再出栈,回到(5,3),往下走,找到刚才的第一个出口为第四条路径,更新最短路径,出栈回到起点。

这就是一个完整的迷宫路程。
看代码:
sum.h
#ifndef __STACK_H__
#define __STACK_H__
#define ROW 10
#define COL 10
typedef int DataType;
typedef struct Coordinate
{
int x;
int y;
}Coordinate;
typedef struct Stack
{
Coordinate cde[40];
int sz;
}Stack;
typedef struct MAP
{
Coordinate cde;
int map[ROW][COL];
}MAP;
void Initstack(Stack * stack);//初始化栈
void Pushstack(Stack * stack, Coordinate d);//压栈
void Popstack(Stack * stack);//出栈
Coordinate Topstack(Stack stack);//栈顶元素
int Lengthstack(Stack* stcak);//栈的长度
void InitMap(MAP* m, Coordinate enter);//初始化地图
void PrintMap(MAP* m);//打印地图
void PassMaze(MAP* m, Coordinate enter, Stack * stack, Stack * shortstack);//走迷宫
int IsValid(MAP* m, Coordinate enter);//判断入口是否有效
int IsPass(MAP* m, Coordinate c,Coordinate d);//判断结点是否能通过
int IsExit(MAP* m, Coordinate d, Coordinate enter);//判断是否是出口
void EvaluateStack(Stack * stack, Stack * shortstack);//更新最短路径
#endif
sum.c
#include<stdio.h>
#include<windows.h>
#include"sum.h"
#include<assert.h>
void Initstack(Stack * stack)
{
assert(stack != NULL);
memset(stack, sizeof(stack->cde), 80);
stack->sz = 0;
}
void Pushstack(Stack * stack, Coordinate d)
{
assert(stack != NULL);
stack->cde[stack->sz] = d;
stack->sz++;
}
void Popstack(Stack * stack)
{
assert(stack != NULL);
Coordinate z;
z.x = 0;
z.y = 0;
stack->cde[stack->sz - 1] = z;
stack->sz--;
}
Coordinate Topstack(Stack stack)
{
return stack.cde[stack.sz - 1];
}
int Lengthstack(Stack* stcak)
{
return stcak->sz;
}
void InitMap(MAP* m, Coordinate enter)
{
assert(m != NULL);
int Map[ROW][COL] = { { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 1, 1, 1, 1, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 0, 1, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 0, 1, 0, 0, 0, 0, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
{ 0, 1, 0, 1, 0, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 1, 0, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 1, 0, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 1, 0, 0, 0, 0, 0, 0 } };
int i, j = 0;
for (i = 0; i < ROW; i++)
{
for (j = 0; j < COL; j++)
{
m->map[i][j] = Map[i][j];
}
}
}
void PrintMap(MAP* m)
{
assert(m != NULL);
int i, j = 0;
for (i = 0; i < ROW; i++)
{
for (j = 0; j < COL; j++)
{
printf("%3d ", m->map[i][j]);
}
printf("\n");
}
}
int IsValid(MAP* m, Coordinate enter)//入口再边界,并且结点的数为1
{
assert(m);
if (enter.x == 0 || enter.y == ROW - 1 || enter.y == 0 || enter.x == COL - 1);
{
if (m->map[enter.x][enter.y] == 1)
return 1;
}
return 0;
}
int IsPass(MAP* m,Coordinate c, Coordinate d)//d必须在地图中,
{
assert(m != NULL);
if (d.x >= 0 && d.x < ROW&&d.y >= 0 && d.y < COL)
{
if (m->map[d.x][d.y] == 1 || (m->map[d.x][d.y]>m->map[c.x][c.y]))//结点为1或者下个结点大于当前结点
return 1;
}
return 0;
}
int IsExit(MAP* m, Coordinate d, Coordinate enter)//出口在边界并且不是入口
{
assert(m != NULL);
if ((d.x == 0 || d.y == ROW - 1 || d.y == 0 || d.x == COL - 1))
{
if (d.x != enter.x||d.y != enter.y)
{
return 1;
}
}
return 0;
}
void EvaluateStack(Stack * stack, Stack * shortstack)
{
assert(stack);
int i, j = Lengthstack(stack);
for (i = 0; i < j; i++)
{
Pushstack(shortstack, stack->cde[i]);
}
}
void PassMaze(MAP* m, Coordinate enter, Stack * stack, Stack * shortstack)
{
assert(m != NULL);
Coordinate cur, next;
Coordinate enter1;
enter1.x = 9;
enter1.y = 1;
if (IsValid(m, enter) == 1)
{
m->map[enter.x][enter.y] = 2;
}
Pushstack(stack, enter);
cur = Topstack(*stack);
//递归的出口
if (IsExit(m, enter, enter1) == 1)
{
if (Lengthstack(stack) > Lengthstack(shortstack)&&shortstack->sz==0)//最短路径的栈为空,说明是第一次走到出口,
{ //找到的第一条路径
EvaluateStack(stack, shortstack);
}
if (Lengthstack(stack) < Lengthstack(shortstack))//当前的栈小于已经保存了最短路径的栈,需要更新最短路径的栈
{
shortstack->sz = 0;
EvaluateStack(stack, shortstack);
}
Popstack(stack);
return;
}
//往上走
next = cur;
next.x = cur.x - 1;
if (IsPass(m, cur, next) == 1)
{
m->map[next.x][next.y] = m->map[cur.x][cur.y] + 1;
PassMaze(m, next, stack, shortstack);
}
//往左走
next = cur;
next.y = cur.y - 1;
if (IsPass(m, cur, next) == 1)
{
m->map[next.x][next.y] = m->map[cur.x][cur.y] + 1;
PassMaze(m, next, stack, shortstack);
}
//往右走
next = cur;
next.y = cur.y + 1;
if (IsPass(m, cur, next) == 1)
{
m->map[next.x][next.y] = m->map[cur.x][cur.y] + 1;
PassMaze(m, next, stack, shortstack);
}
//往下走
next = cur;
next.x = cur.x + 1;
if (IsPass(m, cur, next) == 1)
{
m->map[next.x][next.y] = m->map[cur.x][cur.y] + 1;
PassMaze(m, next, stack, shortstack);
}
//走不通
Popstack(stack);
}
test.c
#include<stdio.h>
#include<windows.h>
#include"sum.h"
int main()
{
MAP m;
Coordinate enter;
Stack stack, shortstack;
Initstack(&stack);
Initstack(&shortstack);
enter.x = 9;
enter.y = 1;
InitMap(&m, enter);
PrintMap(&m);
PassMaze(&m, enter,&stack,&shortstack);
printf("\n");
PrintMap(&m);
printf("最短路径为:\n");
int i,a = shortstack.sz;
for (i = 0; i < a; i++)
{
printf("(%d,%d) ", shortstack.cde[i].x, shortstack.cde[i].y);
}
system("pause");
return 0;
}
最终的结果:
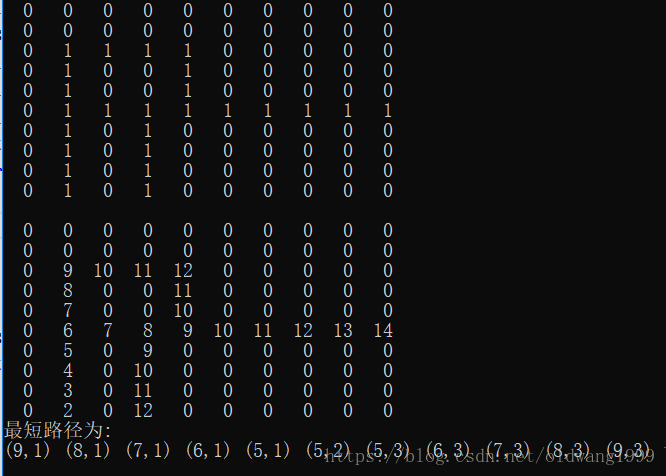





 博客介绍了迷宫求解问题,指出迷宫有多种类型,解法通常采用回溯法。回溯法是将原问题分解为子问题求解,搜索遇阻则回退。以复杂迷宫为例,详细阐述了利用回溯法寻找最短路径的过程,最后给出相关代码文件。
博客介绍了迷宫求解问题,指出迷宫有多种类型,解法通常采用回溯法。回溯法是将原问题分解为子问题求解,搜索遇阻则回退。以复杂迷宫为例,详细阐述了利用回溯法寻找最短路径的过程,最后给出相关代码文件。
















 588
588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








