本课程来自深度之眼,部分截图来自课程视频以及李航老师的《统计学习方法》第二版。
公式输入请参考: 在线Latex公式
前言
任务简介:学习隐马尔科夫模型中的三个基本问题。第10章介绍了隐马尔科夫模型。通过学习第1节,了解隐马尔科夫模型的三要素和三个基本问题;通过学习第2节,理解隐马尔可夫模型概率计算中的前向算法和后向算法;通过学习第3节,掌握维特比算法。
学习目标:
1.了解隐马尔科夫模型的三要素和三个基本问题。
2.掌握隐马尔可夫模型概率计算中的向前算法。
3.理解维特比算法。
4.掌握高斯混合模型的算法实现。
定义
例子就不说了,p193给出定义:
定义10.1(隐马尔可夫模型)隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列,称为状态序列(state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(observation sequence)。序列的每一个位置又可以看作是一个时刻。
这里要注意,之前的朴素贝叶斯模型中对特征的相互关系假设是独立的,而在实际上他们是不独立的,是有相互影响的,隐马尔可夫模型就是考虑了这一点,每一个状态都可能和之前的状态有关系,如果算力足够,当然可以追溯到最起始的状态,但是实际上是无法做到这一点的,因此隐马尔可夫模型在实作的时候只考虑前几个状态。下面简单给出隐马尔可夫模型涉及到的模型参数及符号表达:
状态集合:
Q
=
{
q
1
,
⋯
,
q
N
}
Q=\{q_1,\cdots,q_N\}
Q={q1,⋯,qN}
预测集合:
V
=
{
v
1
,
⋯
,
v
M
}
V=\{v_1,\cdots,v_M\}
V={v1,⋯,vM}
状态序列:
I
=
{
i
1
,
⋯
,
i
T
}
,
i
t
⊂
Q
I=\{i_1,\cdots,i_T\},i_t\subset Q
I={i1,⋯,iT},it⊂Q
预测序列:
O
=
{
o
1
,
⋯
,
o
T
}
,
o
t
⊂
V
O=\{o_1,\cdots,o_T\},o_t\subset V
O={o1,⋯,oT},ot⊂V
状态转移概率矩阵:
A
N
×
N
=
[
a
11
a
11
⋯
a
1
N
a
21
a
22
⋯
a
2
N
⋮
⋮
⋱
⋮
a
N
1
a
N
2
⋯
a
N
N
]
A_{N\times N}=\begin{bmatrix} a_{11} & a_{11} & \cdots & a_{1N}\\ a_{21} & a_{22}& \cdots& a_{2N}\\ \vdots &\vdots & \ddots & \vdots \\ a_{N1} &a_{N2} &\cdots & a_{NN} \end{bmatrix}
AN×N=⎣⎢⎢⎢⎡a11a21⋮aN1a11a22⋮aN2⋯⋯⋱⋯a1Na2N⋮aNN⎦⎥⎥⎥⎤
矩阵中每个值
a
i
j
a_{ij}
aij是从状态
i
i
i转换到状态
j
j
j的概率
| i 2 = q 1 i_2=q_1 i2=q1 | i 2 = q 1 i_2=q_1 i2=q1 | ⋯ \cdots ⋯ | i 2 = q 1 i_2=q_1 i2=q1 | ||
|---|---|---|---|---|---|
| i 1 = q 1 i_1=q_1 i1=q1 | a 11 a_{11} a11 | a 12 a_{12} a12 | ⋯ \cdots ⋯ | a 1 N a_{1N} a1N | a 1 j = p ( i 2 = q j ∣ i 1 = q 1 ) a_{1j}=p(i_2=q_j\mid i_1=q_1) a1j=p(i2=qj∣i1=q1) |
| i 1 = q 2 i_1=q_2 i1=q2 | a 21 a_{21} a21 | a 22 a_{22} a22 | ⋯ \cdots ⋯ | a 2 N a_{2N} a2N | a 2 j = p ( i 2 = q j ∣ i 1 = q 2 ) a_{2j}=p(i_2=q_j\mid i_1=q_2) a2j=p(i2=qj∣i1=q2) |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
| i 1 = q N i_1=q_N i1=qN | a N 1 a_{N1} aN1 | a N 2 a_{N2} aN2 | ⋯ \cdots ⋯ | a N N a_{NN} aNN | a N j = p ( i 2 = q j ∣ i 1 = q N ) a_{Nj}=p(i_2=q_j\mid i_1=q_N) aNj=p(i2=qj∣i1=qN) |
观测概率矩阵:
B
N
×
M
=
[
b
11
b
11
⋯
b
1
M
b
21
b
22
⋯
b
2
M
⋮
⋮
⋱
⋮
a
N
M
a
N
M
⋯
b
N
M
]
B_{N\times M}=\begin{bmatrix} b_{11} & b_{11} & \cdots & b_{1M}\\ b_{21} & b_{22}& \cdots& b_{2M}\\ \vdots &\vdots & \ddots & \vdots \\ a_{NM} &a_{NM} &\cdots & b_{NM} \end{bmatrix}
BN×M=⎣⎢⎢⎢⎡b11b21⋮aNMb11b22⋮aNM⋯⋯⋱⋯b1Mb2M⋮bNM⎦⎥⎥⎥⎤
每个状态能够观测到每个取值的概率:
| o 2 = v 1 o_2=v_1 o2=v1 | o 1 = v 2 o_1=v_2 o1=v2 | ⋯ \cdots ⋯ | o 1 = v M o_1=v_M o1=vM | ||
|---|---|---|---|---|---|
| i 1 = q 1 i_1=q_1 i1=q1 | b 1 ( 1 ) b_{1}(1) b1(1) | b 1 ( 2 ) b_{1}(2) b1(2) | ⋯ \cdots ⋯ | b 1 ( M ) b_{1}(M) b1(M) | b 1 K = p ( o t = v 1 ∣ i t = q 1 ) b_{1}K=p(o_t=v_1\mid i_t=q_1) b1K=p(ot=v1∣it=q1) |
| i 1 = q 2 i_1=q_2 i1=q2 | b 2 ( 1 ) b_{2}(1) b2(1) | b 2 ( 2 ) b_{2}(2) b2(2) | ⋯ \cdots ⋯ | b 2 ( M ) b_{2}(M) b2(M) | b 2 K = p ( o t = v 1 ∣ i t = q 2 ) b_{2}K=p(o_t=v_1\mid i_t=q_2) b2K=p(ot=v1∣it=q2) |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
| i 1 = q N i_1=q_N i1=qN | b N ( 1 ) b_{N}(1) bN(1) | b N ( 2 ) b_{N}(2) bN(2) | ⋯ \cdots ⋯ | b N ( M ) b_{N}(M) bN(M) | b N K = p ( o t = v 1 ∣ i t = q N ) b_{N}K=p(o_t=v_1\mid i_t=q_N) bNK=p(ot=v1∣it=qN) |
初始状态概率向量:
π
=
[
π
1
π
2
⋮
π
N
]
=
[
p
(
i
1
=
q
1
)
p
(
i
1
=
q
2
)
⋮
p
(
i
1
=
q
N
)
]
\pi=\begin{bmatrix} \pi_1\\ \pi_2\\ \vdots\\ \pi_N\end{bmatrix}=\begin{bmatrix} p(i_1=q_1)\\ p(i_1=q_2)\\ \vdots\\ p(i_1=q_N)\end{bmatrix}
π=⎣⎢⎢⎢⎡π1π2⋮πN⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡p(i1=q1)p(i1=q2)⋮p(i1=qN)⎦⎥⎥⎥⎤
就是第一时刻出现每一种状态的初始概率。
模型参数:
λ
=
(
π
N
×
1
,
A
N
×
N
,
B
N
×
M
)
\lambda=(\pi_{N\times 1},A_{N\times N},B_{N\times M})
λ=(πN×1,AN×N,BN×M)
总参数量:
N
×
(
N
×
N
)
×
(
N
×
M
)
N\times(N\times N)\times(N\times M)
N×(N×N)×(N×M)
自由参数量:
(
N
−
1
)
×
(
N
×
N
−
N
)
×
(
N
×
M
−
N
)
(N-1)\times(N\times N-N)\times(N\times M-N)
(N−1)×(N×N−N)×(N×M−N)
模型两个基本假设(模型成立的两个条件):
齐次马尔科夫性:
P
(
i
t
∣
i
t
−
1
,
⋯
,
i
1
)
=
P
(
i
t
∣
i
t
−
1
)
P(i_t|i_{t-1},\cdots,i_{1})=P(i_t|i_{t-1})
P(it∣it−1,⋯,i1)=P(it∣it−1),这个假设是说本来当前状态是和历史状态有关系的,但是这里让其约等于只和前一个状态有关。
观测独立假设:每个观测值之和当前状态有关,和前一个状态无关。
三个基本问题:
概率计算问题:
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ)
学习问题
a
r
g
max
P
(
O
∣
λ
)
arg \max P(O|\lambda)
argmaxP(O∣λ)
预测问题
a
r
g
max
P
(
I
∣
O
,
λ
)
arg \max P(I|O,\lambda)
argmaxP(I∣O,λ)
概率计算问题
先来看第一个问题,在给定参数 λ \lambda λ的条件下,观测序列出现的概率是多少。第一种解决方法是:直接计算法
已知
λ
=
(
A
,
B
,
π
)
,
O
=
{
o
1
,
⋯
,
o
T
}
\lambda=(A,B,\pi),O=\{o_1,\cdots,o_T\}
λ=(A,B,π),O={o1,⋯,oT}
给定参数单条状态链的概率(从初始状态概率乘以第一个状态转第二个状态的概率乘以。。。):
P
(
I
∣
λ
)
=
π
i
1
⋅
a
i
1
i
2
⋅
a
i
2
i
3
⋯
⋅
a
i
T
−
1
i
T
P(I|\lambda)=\pi_{i1}\cdot a_{i_1i_2}\cdot a_{i_2i_3}\cdots\cdot a_{i_{T-1}i_T}
P(I∣λ)=πi1⋅ai1i2⋅ai2i3⋯⋅aiT−1iT
再求出现某状态链的情况下观测序列出现的概率(状态链第一个状态激发第一个观测值的概率乘以状态链第二个状态激发第二个观察值的概率。。。):
P
(
O
∣
I
,
λ
)
=
b
i
1
(
o
1
)
b
i
2
(
o
2
)
⋯
b
i
T
(
o
T
)
P(O|I,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2)\cdots b_{i_T}(o_T)
P(O∣I,λ)=bi1(o1)bi2(o2)⋯biT(oT)
最后算:
P
(
O
,
I
∣
λ
)
=
P
(
O
∣
I
,
λ
)
P
(
I
∣
λ
)
=
π
i
1
⋅
b
i
1
(
o
1
)
a
i
1
i
2
⋅
b
i
2
(
o
2
)
a
i
2
i
3
⋅
b
i
3
(
o
3
)
⋯
a
i
T
−
1
i
T
⋅
b
i
T
(
o
T
)
P(O,I|\lambda)=P(O|I,\lambda)P(I|\lambda)\\ =\pi_{i1}\cdot b_{i_1}(o_1)a_{i_1i_2} \cdot b_{i_2}(o_2)a_{i_2i_3}\cdot b_{i_3}(o_3)\cdots a_{i_{T-1}i_T}\cdot b_{i_T}(o_T)
P(O,I∣λ)=P(O∣I,λ)P(I∣λ)=πi1⋅bi1(o1)ai1i2⋅bi2(o2)ai2i3⋅bi3(o3)⋯aiT−1iT⋅biT(oT)
以上是算一种状态链组合,实际上估计会有很多种状态链的组合,我们可以穷举这块状态链组合,然后求解这些状态链对应的观测链出现的概率,然后把所有观测链出现的概率累加起来。
P
(
O
∣
λ
)
=
∑
I
P
(
O
,
I
∣
λ
)
=
∑
I
P
(
O
∣
I
,
λ
)
P
(
I
∣
λ
)
=
∑
i
1
,
i
2
,
⋯
,
i
T
P
(
O
∣
I
,
λ
)
P
(
I
∣
λ
)
=
∑
i
1
,
i
2
,
⋯
,
i
T
π
i
1
⋅
b
i
1
(
o
1
)
a
i
1
i
2
⋅
b
i
2
(
o
2
)
a
i
2
i
3
⋅
b
i
3
(
o
3
)
⋯
a
i
T
−
1
i
T
⋅
b
i
T
(
o
T
)
P(O|\lambda)=\sum_IP(O,I|\lambda)=\sum_IP(O|I,\lambda)P(I|\lambda)\\ =\sum_{i_1,i_2,\cdots,i_T}P(O|I,\lambda)P(I|\lambda)\\ =\sum_{i_1,i_2,\cdots,i_T}\pi_{i1}\cdot b_{i_1}(o_1)a_{i_1i_2} \cdot b_{i_2}(o_2)a_{i_2i_3}\cdot b_{i_3}(o_3)\cdots a_{i_{T-1}i_T}\cdot b_{i_T}(o_T)
P(O∣λ)=I∑P(O,I∣λ)=I∑P(O∣I,λ)P(I∣λ)=i1,i2,⋯,iT∑P(O∣I,λ)P(I∣λ)=i1,i2,⋯,iT∑πi1⋅bi1(o1)ai1i2⋅bi2(o2)ai2i3⋅bi3(o3)⋯aiT−1iT⋅biT(oT)
这个计算量很大,计算机复杂度:
O
(
T
N
T
)
O(TN^T)
O(TNT)
为了解决这个问题,要用前向算法,下节详细讲。
学习问题:参数估计
1.监督学习方法,就是直接用统计出现频次的方法来求。
已知训练数据包含
S
S
S个长度相同的观测序列和对应的状态序列
{
(
O
1
,
I
1
)
,
(
O
2
,
I
2
)
,
⋯
,
(
O
S
,
I
S
)
}
\{(O_1,I_1),(O_2,I_2),\cdots,(O_S,I_S)\}
{(O1,I1),(O2,I2),⋯,(OS,IS)}
转移概率的
a
i
j
a_{ij}
aij的估计
a
^
i
j
=
A
i
j
∑
j
=
1
N
A
i
j
,
i
=
1
,
2
,
⋯
,
N
;
j
=
1
,
2
,
⋯
,
N
\hat a_{ij}=\cfrac{A_{ij}}{\sum_{j=1}^NA_{ij}},i=1,2,\cdots,N;j=1,2,\cdots,N
a^ij=∑j=1NAijAij,i=1,2,⋯,N;j=1,2,⋯,N
观测概率的
b
j
(
k
)
b_{j}(k)
bj(k)的估计
b
^
j
(
k
)
=
B
j
(
k
)
∑
k
=
1
M
B
j
(
k
)
,
j
=
1
,
2
,
⋯
,
N
;
k
=
1
,
2
,
⋯
,
N
\hat b_{j}(k)=\cfrac{B_{j}(k)}{\sum_{k=1}^MB_{j}(k)},j=1,2,\cdots,N;k=1,2,\cdots,N
b^j(k)=∑k=1MBj(k)Bj(k),j=1,2,⋯,N;k=1,2,⋯,N
初始状态概率的估计
π
i
=
状
态
i
出
现
的
次
数
总
样
本
个
数
\pi_i=\cfrac{状态i出现的次数}{总样本个数}
πi=总样本个数状态i出现的次数
2.无监督学习方法,该方法中没有状态链,只有观测数据。用Buam-Welch算法(EM算法)
输入:观测数据
O
=
(
O
1
,
O
2
,
⋯
,
O
T
)
O=(O_1,O_2,\cdots,O_T)
O=(O1,O2,⋯,OT)
输出:隐马尔可夫模型参数
这里只给大概思路,具体推导不写。
我们知道
P
(
O
,
I
∣
λ
)
=
P
(
O
∣
I
,
λ
)
P
(
I
∣
λ
)
P(O,I|\lambda)=P(O|I,\lambda)P(I|\lambda)
P(O,I∣λ)=P(O∣I,λ)P(I∣λ)
第一步:确定完全数据的对数似然函数
log
P
(
O
,
I
∣
λ
)
\log P(O,I|\lambda)
logP(O,I∣λ)
第二步:E步,求期望(Q函数)
Q
(
λ
,
λ
ˉ
)
=
E
I
[
log
P
(
O
,
I
∣
λ
)
∣
O
,
λ
ˉ
]
Q(\lambda,\bar\lambda)=E_I[\log P(O,I|\lambda)|O,\bar\lambda]
Q(λ,λˉ)=EI[logP(O,I∣λ)∣O,λˉ]
书上化简的过程省略了以下步骤,乘以一个数,除以一个数:
E
I
[
log
P
(
O
,
I
∣
λ
)
∣
O
,
λ
ˉ
]
⋅
P
(
O
,
I
∣
λ
ˉ
)
1
P
(
O
,
I
∣
λ
ˉ
)
E_I[\log P(O,I|\lambda)|O,\bar\lambda]\cdot P(O,I|\bar\lambda)\cfrac{1}{P(O,I|\bar\lambda)}
EI[logP(O,I∣λ)∣O,λˉ]⋅P(O,I∣λˉ)P(O,I∣λˉ)1
最后一项求极值过程由于是常数,可以去掉。
E
I
[
log
P
(
O
,
I
∣
λ
)
∣
O
,
λ
ˉ
]
⋅
P
(
O
,
I
∣
λ
ˉ
)
E_I[\log P(O,I|\lambda)|O,\bar\lambda]\cdot P(O,I|\bar\lambda)
EI[logP(O,I∣λ)∣O,λˉ]⋅P(O,I∣λˉ)
第三步:M步,对Q函数求极大,然后等于0求解。结果不写了。
预测算法
即给定观测序列,求最有可能的对应的状态序列。
其实参数和观测序列已知,所以目标可以写为:
a
r
g
max
P
(
I
∣
O
,
λ
)
arg \max P(I|O,\lambda)
argmaxP(I∣O,λ)
一种是近似算法,一种是维特比算法(后面讲)
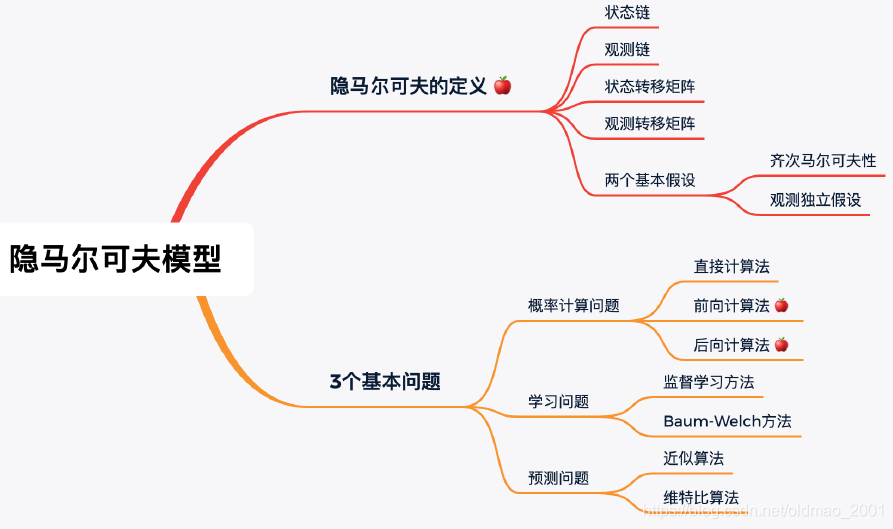
小结
1.状态链、观测链、状态转移矩阵、观测转移矩阵
2.隐马尔可夫两种假设:齐次马尔可夫性、观测独立假设
3.概率计算法:直接计算法、前向算法、后向算法
4.学习算法:EM算法
5.预测算法:近似算法、维特比算法





 本文概述了隐马尔可夫模型的定义,涉及状态转移概率、观测概率矩阵和初始状态概率,重点讲解了概率计算问题的直接法与前向算法,学习问题的参数估计方法,以及预测问题的维特比算法。
本文概述了隐马尔可夫模型的定义,涉及状态转移概率、观测概率矩阵和初始状态概率,重点讲解了概率计算问题的直接法与前向算法,学习问题的参数估计方法,以及预测问题的维特比算法。

















 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










