本课程来自深度之眼,部分截图来自课程视频以及李航老师的《统计学习方法》第二版。
公式输入请参考: 在线Latex公式
导入
为了解决概率计算时间复杂度过高的问题,通常我们使用前向后向结合的算法来求解。最终复杂度为:
O
(
T
N
2
)
O(TN^2)
O(TN2).先引入新变量:
α
t
(
j
)
=
P
(
o
1
,
⋯
,
o
t
i
t
=
q
j
∣
λ
)
,
j
=
1
,
2
,
⋯
,
N
\alpha_t(j)=P(o_1,\cdots,o_ti_t=q_j|\lambda),j=1,2,\cdots,N
αt(j)=P(o1,⋯,otit=qj∣λ),j=1,2,⋯,N
变量的意思是,在
t
t
t时刻为止,观测序列为
o
1
,
o
2
,
⋯
,
o
t
o_1,o_2,\cdots,o_t
o1,o2,⋯,ot,且状态为
q
i
q_i
qi的概率,也叫前向概率。
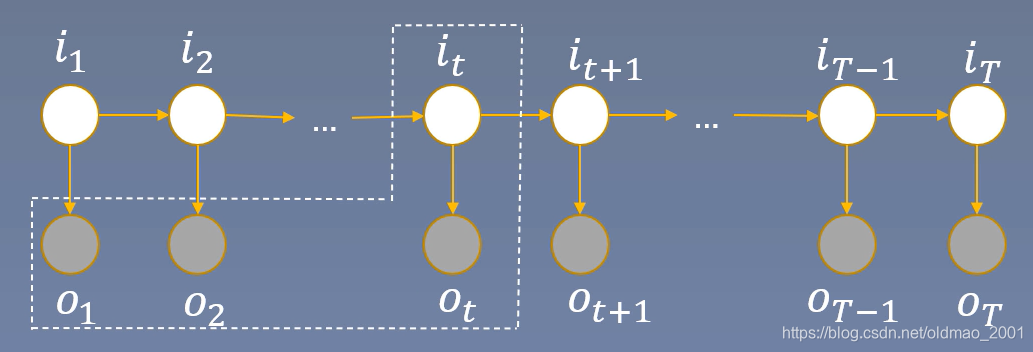
前向算法
输入:隐马尔可夫模型参数
λ
\lambda
λ,观测序列
O
O
O
输出:观测序列概率
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ)
步骤:
1.求初值
α
1
(
i
)
=
π
i
b
i
(
o
1
)
,
,
i
=
1
,
2
,
⋯
,
N
\alpha_1(i)=\pi_ib_i(o_1),,i=1,2,\cdots,N
α1(i)=πibi(o1),,i=1,2,⋯,N
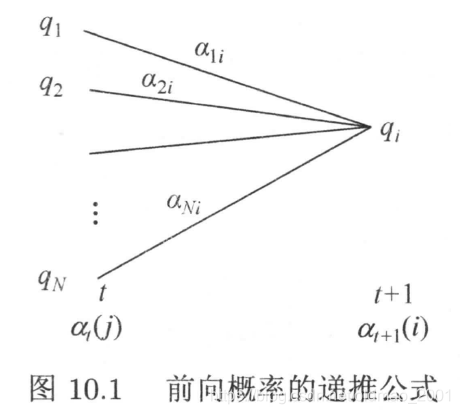
2.递推 对
t
=
1
,
2
,
⋯
,
T
−
1
t=1,2,\cdots,T-1
t=1,2,⋯,T−1
α
t
+
1
(
i
)
=
[
∑
j
=
1
N
α
t
(
j
)
a
j
i
]
b
i
(
o
t
+
1
)
\alpha_{t+1}(i)=\left[\sum_{j=1}^N\alpha_t(j)a_{ji}\right]b_i(o_{t+1})
αt+1(i)=[j=1∑Nαt(j)aji]bi(ot+1)
∑
j
=
1
N
α
t
(
j
)
a
j
i
\sum_{j=1}^N\alpha_t(j)a_{ji}
∑j=1Nαt(j)aji中
a
j
i
a_{ji}
aji表示前一时刻是
q
j
q_j
qj状态,后一个时刻是
q
i
q_i
qi状态;前一时刻状态有N种,所以前一时刻的前向概率
α
t
(
j
)
\alpha_t(j)
αt(j)也有N种。
3.终止
P
(
O
∣
λ
)
=
P
(
o
1
,
⋯
,
o
t
∣
λ
)
=
∑
i
=
1
N
P
(
o
1
,
⋯
,
o
T
,
i
T
=
q
i
∣
λ
)
=
∑
i
=
1
N
α
T
(
i
)
P(O|\lambda)=P(o_1,\cdots,o_t|\lambda)\\ =\sum_{i=1}^NP(o_1,\cdots,o_T,i_T=q_i|\lambda)=\sum_{i=1}^N\alpha_T(i)
P(O∣λ)=P(o1,⋯,ot∣λ)=i=1∑NP(o1,⋯,oT,iT=qi∣λ)=i=1∑NαT(i)
可以理解为最后
T
T
T时刻可嫩会有N种隐藏状态
q
i
q_i
qi,在参数
λ
\lambda
λ的条件下,可能会生成观测值
o
T
o_T
oT,把这N种状态生成观测值
o
T
o_T
oT的概率累加起来。
后向算法
引入变量
β
t
(
i
)
=
P
(
o
t
+
1
,
⋯
,
o
T
∣
i
t
=
q
i
,
λ
)
,
i
=
1
,
2
,
⋯
,
N
\beta_t(i)=P(o_{t+1,\cdots,o_T}|i_t=q_i,\lambda),i=1,2,\cdots,N
βt(i)=P(ot+1,⋯,oT∣it=qi,λ),i=1,2,⋯,N
意思是时刻
t
t
t,状态为
q
i
q_i
qi,参数为
λ
\lambda
λ的条件下,观测序列为:
o
t
+
1
,
⋯
,
o
T
o_{t+1,\cdots,o_T}
ot+1,⋯,oT的概率
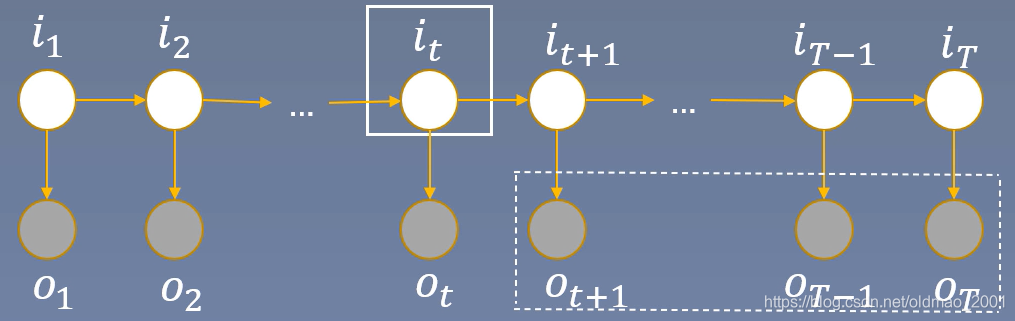
输入:隐马尔可夫模型参数
λ
\lambda
λ,观测序列
O
O
O
输出:观测序列概率
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ)
步骤:
1.求初值
β
T
(
i
)
=
1
,
i
=
1
,
2
,
⋯
,
N
\beta_T(i)=1,i=1,2,\cdots,N
βT(i)=1,i=1,2,⋯,N
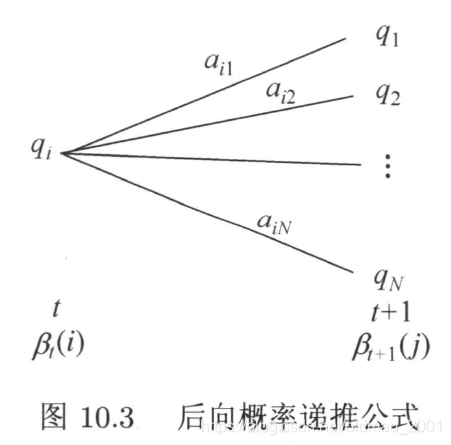
2.递推
β
t
(
i
)
=
∑
j
=
1
N
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
,
i
=
1
,
2
,
⋯
,
N
\beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),i=1,2,\cdots,N
βt(i)=j=1∑Naijbj(ot+1)βt+1(j),i=1,2,⋯,N
3.终止
P
(
O
∣
λ
)
=
∑
i
=
1
N
π
i
b
i
(
o
i
)
β
1
(
i
)
P(O|\lambda)=\sum_{i=1}^N\pi_ib_i(o_i)\beta_1(i)
P(O∣λ)=i=1∑Nπibi(oi)β1(i)





 本文深入介绍了隐马尔可夫模型(HMM)中的前向算法和后向算法,这两种算法用于高效计算观测序列在给定模型条件下的概率。前向算法通过初始化和递推步骤确定在某一时刻之前观测序列的概率,而后向算法则计算从某一时刻开始到序列结束的概率。两者结合能有效解决概率计算的时间复杂度问题,常用于自然语言处理、语音识别等领域。
本文深入介绍了隐马尔可夫模型(HMM)中的前向算法和后向算法,这两种算法用于高效计算观测序列在给定模型条件下的概率。前向算法通过初始化和递推步骤确定在某一时刻之前观测序列的概率,而后向算法则计算从某一时刻开始到序列结束的概率。两者结合能有效解决概率计算的时间复杂度问题,常用于自然语言处理、语音识别等领域。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










