function Hybrid_Iteration_IRL()
% 初始化参数
global Nw N0 N1 Q R tf epsilon hatQ;
Nw = 20; % 值函数基函数数量
N0 = 15; % Hamiltonian常数项基函数数量
N1 = 15; % Hamiltonian控制项基函数数量
Q = diag([1, 1]); % 状态权重矩阵
R = 0.1; % 控制权重
tf = 2.0; % 数据收集时间窗口
epsilon = 1e-4; % 收敛阈值
hatQ = @(x) 10*(x'*Q*x) + 0.1*(x(1)^4 + x(2)^4); % 辅助Q函数
% 基函数初始化（多项式基）
phi = @(x) [x(1)^2; x(1)*x(2); x(2)^2; x(1)^4; x(1)^3*x(2);
x(1)^2*x(2)^2; x(1)*x(2)^3; x(2)^4; x(1)^6; x(2)^6;
x(1)^5*x(2); x(1)^4*x(2)^2; x(1)^3*x(2)^3;
x(1)^2*x(2)^4; x(1)*x(2)^5; x(1)^8; x(2)^8;
x(1)^7*x(2); x(1)^6*x(2)^2; x(1)^5*x(2)^3];
psi0 = @(x) [x(1); x(2); x(1)^2; x(1)*x(2); x(2)^2;
x(1)^3; x(1)^2*x(2); x(1)*x(2)^2; x(2)^3];
psi1 = @(x) [x(1); x(2); x(1)^2; x(1)*x(2); x(2)^2];
% 权重初始化
w = randn(Nw, 1); % 值函数权重
c0 = zeros(N0, 1); % Hamiltonian常数项权重
c1 = zeros(N1, 1); % Hamiltonian控制项权重
% 主循环参数
max_iter = 100;
iter = 1;
phase1_complete = false;
% 状态初始化
x0 = [1.0; -0.5];
x = x0;
% 数据存储
X_data = []; U_data = [];
% 混合迭代主循环
while iter <= max_iter
%% 阶段1: 学习可行策略 (VI风格)
if ~phase1_complete
% 应用探索噪声 (多正弦信号)
tspan = linspace(0, tf, 100);
[T, X] = ode45(@(t,x) sysDynamics(t, x, explorationNoise(t)), tspan, x);
% 存储数据
for k = 1:length(T)
u_explore = explorationNoise(T(k));
X_data = [X_data; X(k,:)];
U_data = [U_data; u_explore];
end
% 更新Hamiltonian权重
[c0, c1] = updateHamiltonianWeights(X_data, U_data, w, psi0, psi1);
% 更新值函数权重
w_new = updateValueWeights(X_data, U_data, w, c0, c1, phi);
% 检查切换条件
w_diff = norm(w_new - w);
if w_diff < epsilon && isPositiveDefinite(w, phi, X_data)
phase1_complete = true;
u_feasible = @(x) -0.5*R^-1 * (c1'*psi1(x));
fprintf('切换到阶段2在迭代: %d\n', iter);
end
w = w_new;
x = X(end,:)'; % 更新状态
%% 阶段2: 策略迭代 (PI风格)
else
% 策略评估: 固定策略下求解值函数
w_new = policyEvaluation(u_feasible, x, phi);
% 策略改进: 更新控制策略
c1_new = policyImprovement(w_new, X_data, psi1);
% 检查收敛
if norm(c1_new - c1) < epsilon
fprintf('在迭代 %d 收敛\n', iter);
break;
end
w = w_new;
c1 = c1_new;
u_feasible = @(x) -0.5*R^-1 * (c1'*psi1(x));
% 收集新数据
tspan = linspace(0, tf, 100);
[T, X] = ode45(@(t,x) sysDynamics(t, x, u_feasible(x)), tspan, x);
for k = 1:length(T)
X_data = [X_data; X(k,:)];
U_data = [U_data; u_feasible(X(k,:)')];
end
x = X(end,:)';
end
iter = iter + 1;
end
%% 可视化结果
plotResults(X_data, U_data);
end
%% 辅助函数
function dx = sysDynamics(t, x, u)
% 示例系统: 修改为实际系统
dx = [x(2) + 0.5*x(1)*cos(x(1));
-x(1) + x(2) - x(2)*(x(1)^2 + x(2)^2) + u];
end
function u = explorationNoise(t)
% 探索噪声 (多正弦信号)
u = 0.5*(sin(0.5*t) + 0.8*cos(1.2*t) + 0.3*sin(2.3*t));
end
function [c0_new, c1_new] = updateHamiltonianWeights(X, U, w, psi0, psi1)
% 最小二乘法更新Hamiltonian权重
A = []; b = [];
for k = 1:size(X,1)
x = X(k,:)'; u = U(k);
dV = gradientPhi(x)' * w; % 梯度∇V
dVdt = dV' * sysDynamics(0, x, u); % dV/dt
psi_vec = [psi0(x); psi1(x)*u; u^2];
A = [A; psi_vec'];
b = [b; -dVdt - hatQ(x)];
end
weights = pinv(A) * b;
c0_new = weights(1:length(psi0(x)));
c1_new = weights(length(psi0(x))+1:end-1);
end
function w_new = updateValueWeights(X, U, w, c0, c1, phi)
% 值函数权重更新 (VI风格)
H_hat = @(x,u) c0'*psi0(x) + (c1'*psi1(x))*u + u^2;
A = []; b = [];
for k = 1:size(X,1)-1
x = X(k,:)'; u = U(k);
x_next = X(k+1,:)';
delta_phi = phi(x_next) - phi(x);
A = [A; delta_phi'];
b = [b; -integral(@(t) runningCost(x,u), 0, tf)];
end
w_new = pinv(A) * b;
end
function w_new = policyEvaluation(u_policy, x0, phi)
% 策略评估: 固定策略下求解值函数
tspan = linspace(0, tf, 100);
[~, X] = ode45(@(t,x) sysDynamics(t, x, u_policy(x)), tspan, x0);
A = []; b = [];
for k = 1:size(X,1)-1
x = X(k,:)'; u = u_policy(x);
x_next = X(k+1,:)';
delta_phi = phi(x_next) - phi(x);
A = [A; delta_phi'];
b = [b; -integral(@(t) runningCost(x,u), 0, tf)];
end
w_new = pinv(A) * b;
end
function c1_new = policyImprovement(w, X, psi1)
% 策略改进: 更新控制策略权重
A = []; b = [];
for k = 1:size(X,1)
x = X(k,:)';
grad_phi = gradientPhi(x); % 基函数梯度
A = [A; (grad_phi' * w) * psi1(x)'];
b = [b; -2*R * u_optimal(x, w, psi1)];
end
c1_new = pinv(A) * b;
end
function u = u_optimal(x, w, psi1)
% 最优控制计算
grad_V = gradientPhi(x)' * w;
u = -0.5 * R^-1 * grad_V(2); % 假设g(x)=[0;1]
end
function cost = runningCost(x, u)
% 运行成本
cost = x'*Q*x + u'*R*u;
end
function grad = gradientPhi(x)
% 基函数梯度 (示例)
grad = [2*x(1), x(2), 0;
x(2), x(1), 2*x(2)]; % 需扩展为实际基函数
end
function pdf = isPositiveDefinite(w, phi, X)
% 检查值函数是否正定 (简化实现)
pdf = all(arrayfun(@(i) phi(X(i,:)')'*w > 0, 1:size(X,1)));
end
function plotResults(X, U)
% 结果可视化
figure;
subplot(3,1,1); plot(X(:,1)); title('状态 x1');
subplot(3,1,2); plot(X(:,2)); title('状态 x2');
subplot(3,1,3); plot(U); title('控制输入 u');
figure;
plot(X(:,1), X(:,2));
xlabel('x1'); ylabel('x2'); title('相轨迹');
grid on;
end
解释一下这段代码
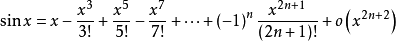
该博客详细介绍了如何利用麦克劳林公式计算正弦函数sin(x)的近似值，确保截断误差小于0.5*10^-13，特别强调了对长double类型精度的要求和求解过程。
扫一扫
869
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
