【线性DP】DTOJ 5022 游戏

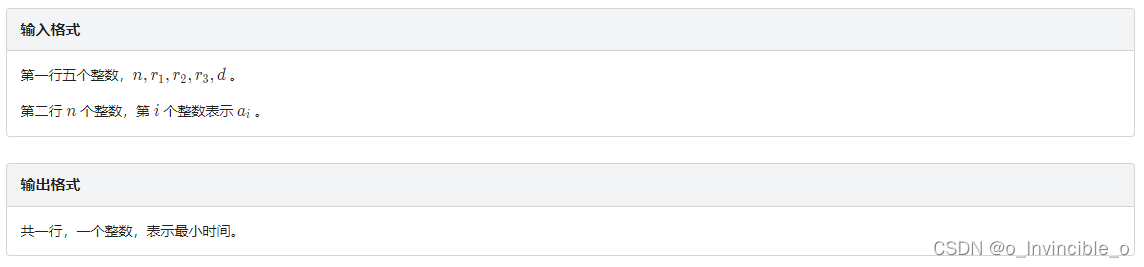
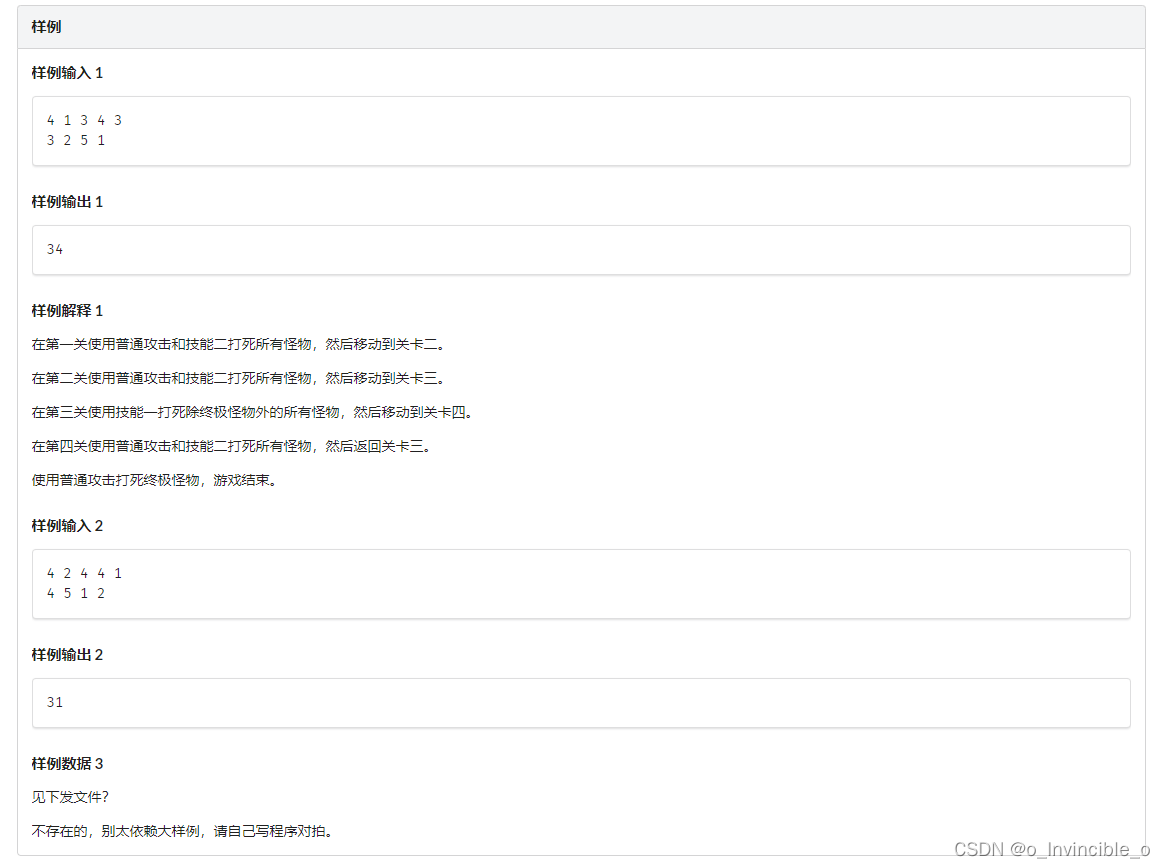
题目描述

---

Solution

先证明一个引理：

对于前 $i$ 关，若被迫传送（没打死BOSS），则必然会在进入 $i+2$ 关之前（第 $i+1$ 关结束或者被传送）打死第 $i$ 关的BOSS。

首先，如果我们一直向后传送，到了非结尾的位置 $j(j>i,j\ne n)$ ，返回解决 $i$ 的BOSS，这样 $[i,j]$ 的路程就要折返两趟，结果肯定不如在进入在进入 $i+2$ 关之前解决更优。

其次，如果存在另一种方案，在每一关都使用技能1，被迫传送，到了最后一关在返回解决所有BOSS，如下图，可以看出这种方案可以等价转换为第二种方案：

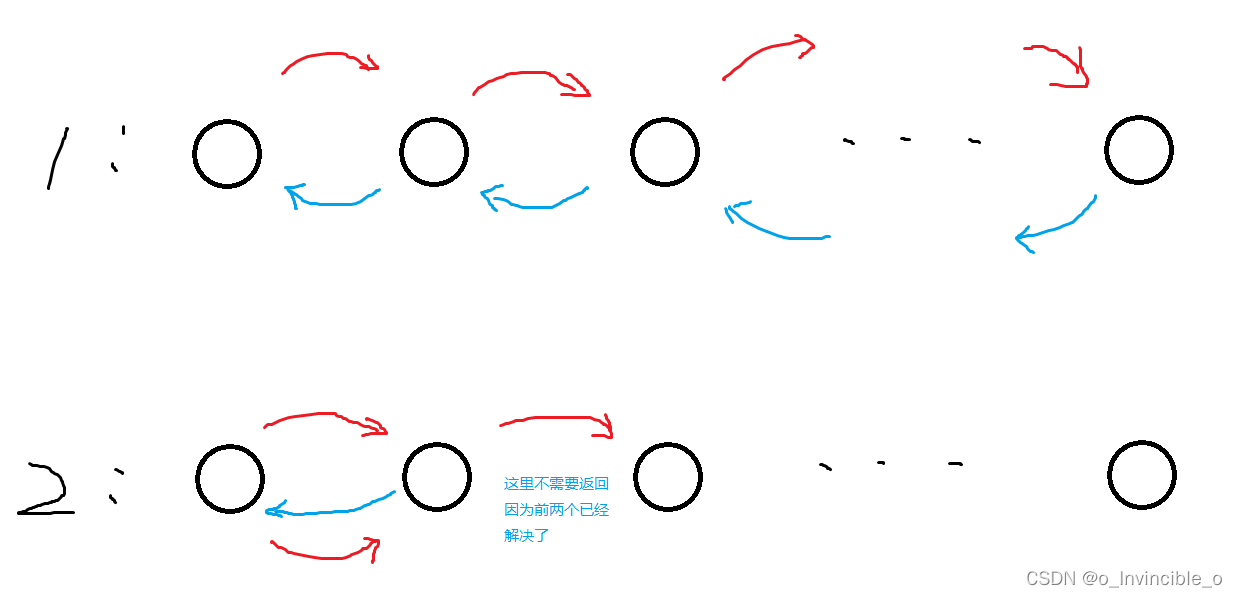
所以引理成立。

因此我们可以考虑 $dp$ ：

观察上面的2方案，可以发现我们其实是将关卡两两考虑，每个关卡可以和前后两个关卡分别配对，对于每两个关卡，我们有如下4种方案：

• 解决1的BOSS，解决2的BOSS
• 打掉1的BOSS一条血，解决2的BOSS，再回去解决1
• 打掉1的BOSS一条血，打掉2的BOSS一条血，回去解决1，再回来解决2
• 也可以不解决2的BOSS，只打掉一条血，但1的BOSS必须解决（根据引理），和下一关配对或传送回上一关再回来，后者只对于在最后一关的时候

所以，设 $f[i][0/1]$ 表示在第 $i$ 关，BOSS已解决/未解决时的最小代价，则根据上面四种情况可以列出转移方程，$get(i,0/1)$ 表示对于 $i$ 的BOSS，解决掉/只打掉一条血所需的代价：

$$f[i][0]=\min \{\begin{array}{l}f[i-1][0]+d+get(i,0)\\ f[i-1][1]+d+get(i,0)+d+r_1+[i\ne n]\ast d\\ f[i-1][0]+d+get(i,1)+2\ast (d+r_1)\end{array}$$
$$f[i][1]=f[i-1][0]+d+get(i,1)$$

---

Code

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define int long long
using namespace std;

const int N = 1e6 + 5;

int n, r1, r2, r3, d;
int a[N], f[N][2];

int get(int i, bool op)
{
	if(op == 0) return a[i] * r1 + r3;
	return min(r2, a[i] * r1 + r1);
}

signed main()
{
	scanf("%lld%lld%lld%lld%lld", &n, &r1, &r2, &r3, &d);
	for(register int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);
	f[1][0] = get(1, 0);
	f[1][1] = get(1, 1);
	for(register int i = 2; i <= n; i ++ )
	{
		int p = f[i - 1][1] + d + get(i, 0) + d + r1 + (i == n ? 0 : d);
		int q = f[i - 1][1] + d + get(i, 1) + 2 * (d + r1) ;
		f[i][0] = min(f[i - 1][0] + get(i, 0) + d, min(p, q));
		f[i][1] = f[i - 1][0] + get(i, 1) + d;
	}
	printf("%lld\n", min(f[n][0], f[n][1] + 2 * d + r1));
	return 0;
}