手把手教你电机FOC控制【三】

范子琦

已于 2022-09-18 16:39:54 修改

阅读量4k

点赞数 3

分类专栏： FOC 文章标签：单片机嵌入式硬件

于 2022-09-18 16:38:48 首次发布

本文链接：https://blog.youkuaiyun.com/oXiaoLingTong/article/details/126919391

版权

FOC 专栏收录该内容

4 篇文章

订阅专栏

手把手教你电机FOC控制【三】

文章作者: 范子琦
文章链接: https://www.robotsfan.com/posts/d99d1c1a.html
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自范子琦的博客！

电流闭环

经过前文的反Park变换、SVPWM、定时器与全桥，输入的 $U_{d}$ 和 $U_{q}$ 最终转换为三相电压输出到电机。如果需要让电机以设定的电流值运行，就需要使用PI控制器闭环控制电流。但三相交流电流是不太容易实现闭环控制的，所以我们选择对直流电流 $I_{d}$ 和 $I_{q}$ 进行闭环控制。

PI控制器输入目标参考电流 $I_{d_{ref}}$ 和 $I_{q_{ref}}$ ，输出 $U_{d}$ 和 $U_{q}$ ，现在还缺少反馈量 $I_{d}$ 和 $I_{q}$ ，这就需要用到前文讲到的Park与Clark正变换。安装采样电阻，用单片机的ADC采集全桥上任意两相的电流，通过基尔霍夫电流定律可计算第三相的电流，通过Clark变换计算出 $I_{\alpha}$ 和 $I_{\beta}$ ，再通过Park变换计算出反馈量 $I_{d}$ 和 $I_{q}$ 。

对于PI控制器参数的设定，以下为一个参考值（但还是需要自行调整）：
$\begin{array}{c} & P & I &\\ d& K_{pd}=\alpha L_d & K_{Id}=\alpha R\\ q& K_{pq}=\alpha L_q & K_{Iq}=\alpha R \end{array}$
其中 $\alpha$ 的取值为：（其中 $\tau$ 为电机的时间常数）
$\alpha = \frac{2\pi}{\tau} \\ \tau = min\left\{\frac{L_d}{R},\frac{L_q}{R}\right\}$
电机分为表贴电机和内嵌式电机，表贴式电机的永磁体贴在转子表面，内嵌式电机的永磁体安装在转子内。我们常用的电机都是表贴电机，对于表贴电机， $L_d=L_q=L$ ，则可以得到PI控制器的参考参数：
$K_{p}=2\pi R \\ K_{I}=2\pi \frac{R^2}{L}$

角度和速度的获取

有感（HALL）

霍尔传感器分为60度和120度

画一下转一圈三个霍尔传感器的波形

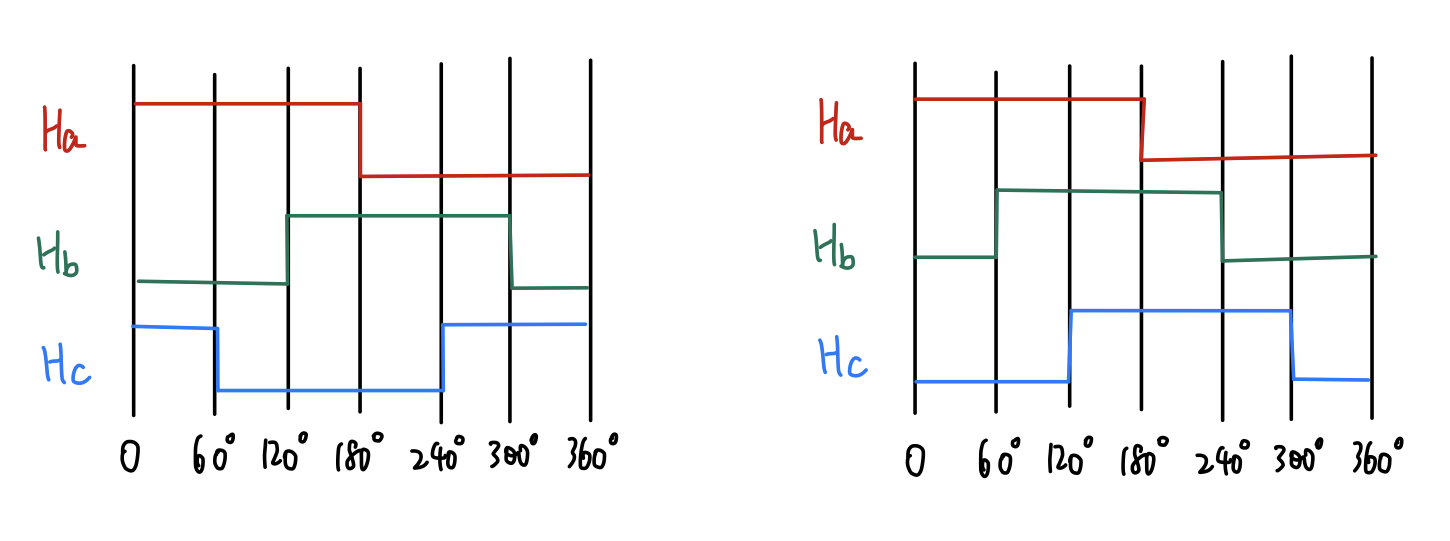
可以看到，这两种排列方式除了组合方式不同，其他都一样。

单片机通过输入捕获采集三路高低电平的跳变，通过对三路信号进行异或，则转一圈可以进6次中断，进入中断后检测IO电平就可以知道电机对应角度。但现在一圈只能获取到6个固定的角度值，无法获取到如80度这个角度。这时可以对速度进行积分得到角度，速度的获取可以通过查询60-120之间定时器的计数值来获得。但是转到80度的时候没办法获取到120度时候的定时器计数值就无法获取当前段的速度，这时可以用前一段的速度近似为当前段的速度。

无感（EKF）

引入

前面的有感部分，是在电机上安装霍尔传感器，引出三根线到单片机通过输入捕获算出当前角度，再与预设角度完成角度闭环。

而无感控制则不需要霍尔传感器，只需要三根UVW线输出到电机即可，去掉了霍尔传感器和三根线，节省了成本；有些使用场合无法使用霍尔传感器，则需要使用无感，比如空调压缩机，内部充满了润滑油，无法安装霍尔传感器；有些时候有感算法或硬件出现问题也可以切换至无感，防止系统闸机，比如汽车运行中霍尔传感器突然坏了，为了使整个系统正常运行，就可以临时切换到无感。上述这些都是无感控制的优点。无感控制现在已经越来越普及，空调、洗衣机、高端风扇、汽车都在用无感控制。

状态观测器

观测器有很多种，扩展卡尔曼滤波观测器、滑膜观测器、龙伯格观测器、自适应观测器、磁链观测器等。其中扩展卡尔曼滤波观测器的低速性能比较好，所以本文重点讨论EKF。

状态观测器实质上就是用数学方法建立一个可以模拟真实被控对象的模型，用这个模型来得知一些无法通过测量得到的状态量。对于电机系统来说，如果没有传感器去测量电机的转速和转子位置，那么就可以通过搭建状态观测器来估算电机的转子和转子位置，这就是基于状态观测器的电机的无传感器控制。

但是使用这种方法建立的观测器有着诸多问题：

抗干扰能力差：加入扰动或负载，此时的状态观测器很难保持正确的响应而导致输出错误或者系统崩溃；
存在误差：误差主要存在与系统误差和测量误差
1. 系统误差：在建模的时候电机的参数不可能完全精确，在建模的时候造成误差。
2. 测量误差：观测器需要电流作为输入，而电流的采集就会存在误差。

所以为了解决以上问题，需要给状态观测器增加反馈，通过反馈来修正状态观测器的输出，让观测器尽可能的去贴近真实的电机。

在这里插入图片描述

状态空间表示

线性系统的状态空间方程为：
$\left\{\begin{array}{l} \dot x = Ax+Bu\\ y=Hx \end{array}\right.$
永磁同步电机的方程：
$\left\{\begin{array}{l} U_\alpha = Ri_\alpha + L_s \frac{di_\alpha}{dt} - \omega_e \psi_f sin\theta\\ U_\beta = Ri_\beta + L_s \frac{di_\beta}{dt} + \omega_e \psi_f cos\theta \end{array}\right.$
上述方程的含义为：将每一相抽象为一个电阻，一个电感和一个反电动势的串联，则每一相的电压为前面三项压降之和（反电动势为速度乘磁链）。方程中的电阻R、电感L、和磁链flux为电机的固有参数，电流可以通过采样电阻得到，只剩下了角度和转速，将电机方程转化为状态空间表达：
$\left\{\begin{array}{l} \frac{d i_\alpha}{dt} = -\frac{R}{L_s}i_\alpha + \frac{1}{L_s}\omega_e\psi_f sin\theta + \frac{1}{L_s}U_\alpha \\ \frac{d i_\beta}{dt} = -\frac{R}{L_s}i_\beta - \frac{1}{L_s}\omega_e\psi_f cos\theta + \frac{1}{L_s}U_\beta \\ \frac{d \omega_e}{dt} = 0 \\ \frac{d \theta}{dt} = \omega_e \end{array}\right.$

矩阵化表示

接下来我们将上面的式子整理成矩阵形式，首先确认状态变量分别为 $ \dot{i_\alpha},\dot{i_\beta},\dot{\omega_e},\dot{\theta}$ ，则有：
$\begin{aligned} \dot{x}= \begin{bmatrix} \dot{i_\alpha} \\ \dot{i_\beta} \\ \dot{\omega_e} \\ \dot{\theta} \\ \end{bmatrix} \quad x= \begin{bmatrix} i_\alpha \\ i_\beta \\ \omega_e \\ \theta \\ \end{bmatrix} \end{aligned}$
输入 $u$ ，对于电机来说就是电压，我们选择 $\alpha-\beta$ 坐标系：
$\begin{aligned} u= \begin{bmatrix} U_\alpha \\ U_\beta \\ \end{bmatrix} \end{aligned}$
输出矩阵 $y$ 为通过采样电阻测得的电流：
$\begin{aligned} y= \begin{bmatrix} i_\alpha \\ i_\beta \\ \end{bmatrix} \end{aligned}$
则 $H$ 和 $B$ 矩阵就可以表示为：
$\begin{aligned} H= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} \quad B= \begin{bmatrix} \frac{1}{L_s} & 0 \\ 0 & \frac{1}{L_s} \\ 0 & 0 \\ 0 & 0 \\ \end{bmatrix} \end{aligned}$
此时矩阵形式的表示为：
$\begin{aligned} \begin{bmatrix} i_{\alpha} \\ \dot{i}_{\beta} \\ \dot{\omega} \\ \dot{\theta} \end{bmatrix} & = \begin{bmatrix} -\frac{R}{L_{S}} i_{\alpha}+\frac{1}{L_{s}} \omega_{e} \psi_{f} \sin \theta \\ -\frac{R}{L_{S}} i_{\beta}-\frac{1}{L_{s}} \omega_{e} \psi_{f} \cos \theta \\ 0 \\ \omega_{e} \end{bmatrix}+\begin{bmatrix} \frac{1}{L_{s}} & 0 \\ 0 & \frac{1}{L_{s}} \\ 0 & 0 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} u_{\alpha} \\ u_{\beta} \end{bmatrix}\\ \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} & = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \\ \omega_{e} \\ \theta \end{bmatrix} \end{aligned}$
对比状态空间表示，无法显式地表示出线性的 $A x$ ，因为电机系统不是线性的，所以用 $f (x)$ 这一非线性项替代这一项。 $f (x)$ 定义为：
$\begin{aligned} f(x)= \begin{bmatrix} -\frac{R}{L_s}i_\alpha + \frac{1}{L_s}\omega_e\psi_f sin\theta \\ -\frac{R}{L_s}i_\beta - \frac{1}{L_s}\omega_e\psi_f cos\theta \\ 0 \\ \omega_e \\ \end{bmatrix} \end{aligned}$
则此时的状态空间方程变为：
$\left\{\begin{array}{l} \dot x = f(x)+Bu\\ y=Hx \end{array}\right.$

扩展卡尔曼滤波器

关于卡尔曼滤波器的知识请看这篇文章：手撕卡尔曼滤波器

扩展卡尔曼滤波器（Extend Kalman Filter），简称EKF。带“扩展”二字，是因为卡尔曼滤波器只能处理线性系统，而电机是一个非线性，强耦合的系统，使用扩展卡尔曼滤波器可以处理这种非线性系统。

前文的状态空间方程中 $f (x)$ 是非线性的，如果想对非线性系统进行卡尔曼滤波，需要对其线性化（Linearization），泰勒级数展开是将非线性系统线性化的一种方法。将 $f (x)$ 泰勒级数展开并取前两项：
$\begin{aligned} f(x)=f(x_0)+\frac{\partial f(x)}{\partial x}(x-x_0) \end{aligned}$
对 $f (x)$ 求偏导：
$\begin{aligned} F = \frac{\partial f(x)}{\partial x}= \begin{bmatrix} -\frac{R}{L_{S}} & 0 & \frac{\psi_{f} \sin \theta}{L_{S}} & \frac{\omega_{e} \psi_{f} \cos \theta}{L_{S}} \\ 0 & -\frac{R}{L_{S}} & -\frac{\psi_{f} \cos \theta}{L_{S}} & \frac{\omega_{e} \psi_{f} \sin \theta}{L_{S}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \end{aligned}$
此时状态空间方程变为：
$\dot{x}=f(x_{0})+F(x-x_{0})+B u$
状态方程是建立在连续系统的基础上，需要将其转化成离散化系统后，才能在微控制器中实现卡尔曼滤波状态观测器。在离散化系统中， $\dot{x}=\frac{x_{k}-x_{k-1}}{\Delta t}$ ，则状态空间方程表示为：
$\begin{aligned} \frac{x_{k}-x_{k-1}}{\Delta t} &= f(x_{k-1})+B u_{k-1}\\ x_{k}&=x_{k-1}+(f(x_{k-1})+B u_{k-1}) \Delta t\\ &=(I+F\Delta t)x_{k-1}+B u_{k-1}\Delta t \end{aligned}$
令 $A=(I+F\Delta t)$ ，扩展卡尔曼滤波器的流程为以下五步：

预测
1. 计算预估值
  
  $\hat{x}_k^-=\hat{x}_{k-1}+(f(x_{k-1})+B u_{k-1}) \Delta t$
2. 计算误差协方差
  
  $P_k^-=(I+F\Delta t)P_{k-1}(I+F\Delta t)^T+Q$
校正
1. 计算卡尔曼增益
  
  $K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}$
2. 修正预估值
  
  $\hat{x}_k=\hat{x}_k^- + K_k(z_k-H\hat{x}_k^-)$

更新误差协方差，用于下一次计算

$P_k=(I-K_kH)P_k^-$

上面的五个方程中， $\Delta t$ 为采样时间， $Q$ 为模型误差， $R$ 为测量误差

在MATLAB中建立EKF观测器，需要建立全局变量x和P用于保存每一次迭代的值给下一次迭代使用：

function x_posteriori  = fcn(Ialpha,Ibeta,Ualpha,Ubeta,Ls,Rs,Flux)

global x;
global P;

R=[0.02,0;0,0.02];
Q=[0.01,0,0,0;0,0.01,0,0;0,0,0.01,0;0,0,0,0.01];
Time=0.0001;

u=[Ualpha;Ubeta];
y=[Ialpha;Ibeta];
H=[1,0,0,0;0,1,0,0];
B=[1/Ls,0;0,1/Ls;0,0;0,0];
F=[-Rs/Ls,0,Flux*sin(x(4,1))/Ls,x(3,1)*Flux*cos(x(4,1))/Ls;0,-Rs/Ls,-Flux*cos(x(4,1))/Ls,x(3,1)*Flux*sin(x(4,1))/Ls;0,0,0,0;0,0,1,0];
f=[-Rs*Ialpha/Ls+x(3,1)*Flux*sin(x(4,1))/Ls;-Rs*Ibeta/Ls-x(3,1)*Flux*cos(x(4,1))/Ls;0;x(3,1)];
% 计算预估值
x_prior=x+(f+B*u)*Time;
% 计算误差协方差
A=(eye(4)+F*Time);
P_prior=A*P*A'+Q;
% 计算卡尔曼增益
K=(P_prior*H')/(H*P_prior*H'+R);
% 修正预估值
x_posteriori=x_prior+K*(y-H*x_prior);
% 更新误差协方差
P_posteriori=(eye(4)-K*H)*P_prior;

if x_posteriori(4,1)>(2*pi)
    x_posteriori(4,1)=x_posteriori(4,1)-(2*pi);
end

x=x_posteriori;
P=P_posteriori;

调整R矩阵和Q矩阵至最优，查看观测器效果：

蓝色为观测角度，黄色为真实角度。可以看到经过很短时间的迭代，观测器就已经可以很好地预测电机角度，至此完成了EKF无感算法。

速度闭环

前文电流闭环精准地控制了电机电流从而控制转矩，但要想精确地控制电机的速度就需要进行速度闭环。速度闭环是在电流闭环的外环，控制Id=0，通过前面有感或无感获取到的速度与速度参考作比较，通过PID控制Iq的值。

对于速度闭环PID，一班只是用PD控制。 $K_p$ 和 $K_d$ 的理论计算值为：
$K_P=\frac{\beta J}{1.5P\psi_f}\\ K_I=\beta K_P$
其中 $\beta$ 是速度环的带宽，一般为50rad/s； $J$ 为电机转动惯量，是电机的固有参数； $P$ 是电机的极对数； $\psi_f$ 是电机的磁链。