leetcode skyline problem

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

- lefti is the x coordinate of the left edge of the ith building.
- righti is the x coordinate of the right edge of the ith building.
- heighti is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],…]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, […,[2 3],[4 5],[7 5],[11 5],[12 7],…] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: […,[2 3],[4 5],[12 7],…]

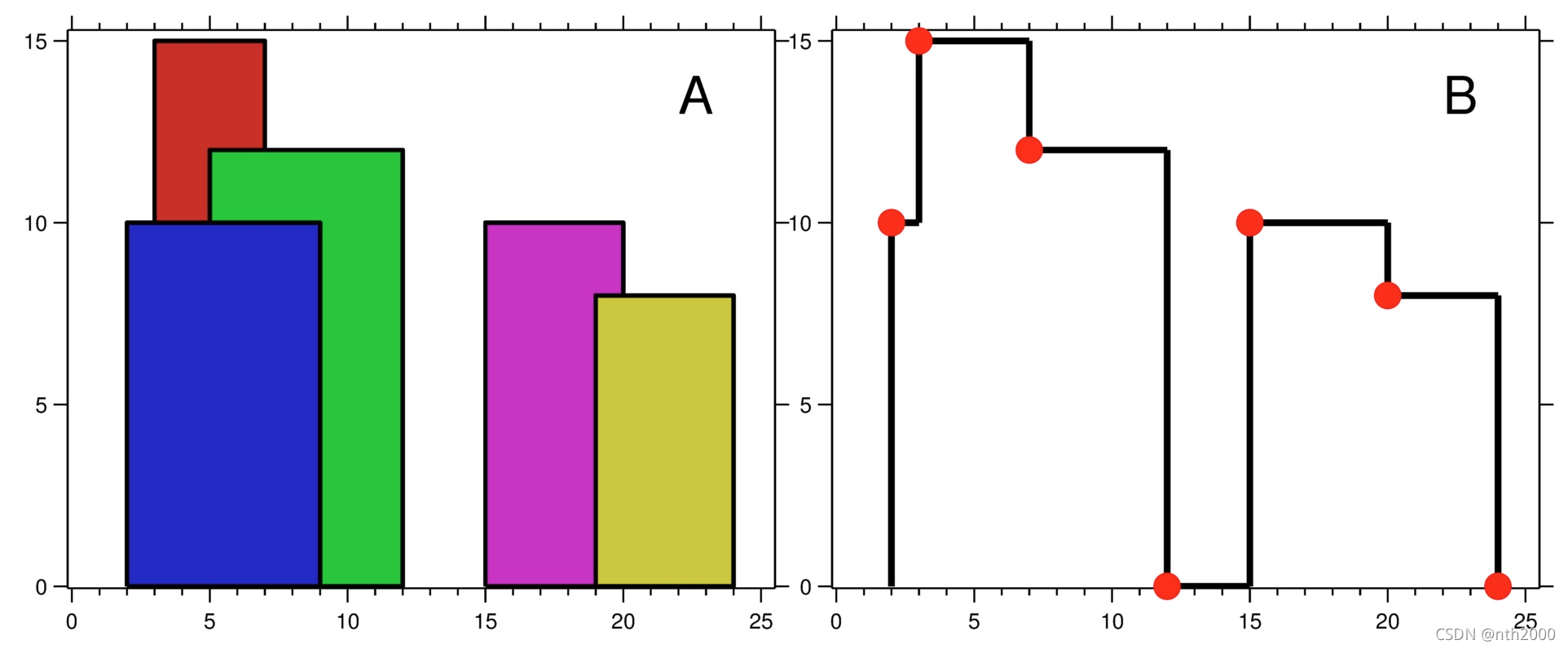
• 显然仅考虑建筑物的边界横坐标
• 维护一个优先队列，从小到大遍历每一个横坐标
  • 在优先队列中加入每一个以该横坐标为左边界的建筑物
  • 从堆中不断弹出边界右横坐标小于等于该横坐标的建筑物
    • 这里必须是小于等于而不是像上面步骤中的等于
    • 因为堆中存在被其余最大值掩盖了的而未被弹出的元素，即在该横坐标下应该从堆中删除，但是由于堆顶元素很大就导致它没有被删除，有可能之后会再次遇到它
  • 现在堆中的堆顶元素即为所求，如果堆为空，则结果为0
• 注意官方代码中的简洁性

算法分析：每一个元素最多入堆一次，出堆一次，因此复杂度为$O(nlog(n))$
我的代码：

class Solution {


    public List<List<Integer>> getSkyline(int[][] buildings) {
        //大顶堆，第一个元素保存建筑物右下标，第二个元素保存高度
        PriorityQueue<int[]> q = new PriorityQueue<>(new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return -Integer.compare(o1[1],o2[1]);
            }
        })    ;
        List<Integer> boundaries = new ArrayList<>();  //所有边缘的横坐标值
        for(int i = 0;i<buildings.length;i++)
        {
            boundaries.add(buildings[i][0]);
            boundaries.add(buildings[i][1]);
        }
        //排序
        boundaries.sort(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return Integer.compare(o1,o2);
            }
        });
        int idx = 0;
        List<List<Integer>> ans = new ArrayList<>();
        for(int i = 0;i<boundaries.size();i++)
        {
            //弹出不满足条件的元素
            //这里必须用<=，因为前面的元素还有可能没有弹出
            while(!q.isEmpty() && q.peek()[0]<=boundaries.get(i))
            {
                q.poll();
            }
            //加入元素
            //不用惧怕重复，因为第一次已经全部加入了
            while(idx < buildings.length && buildings[idx][0] == boundaries.get(i))
            {
                q.add(new int[]{buildings[idx][1],buildings[idx][2]});
                idx++;
            }
            if(i!=0 && (Objects.equals(ans.get(ans.size() - 1).get(0), boundaries.get(i)) || (!q.isEmpty()&&ans.get(ans.size() - 1).get(1) == q.peek()[1] )))
            {
            }
            else{
                List<Integer> temp = new ArrayList<>();
                temp.add(boundaries.get(i));
                if(!q.isEmpty())
                {
                    temp.add(q.peek()[1]);
                }
                else temp.add(0);
                ans.add(temp);
            }
            Arrays.asList(1,2,3,4,5);;
        }
        return ans;
    }

}




官方代码：
```java
class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> b[1] - a[1]);
        List<Integer> boundaries = new ArrayList<Integer>();
        for (int[] building : buildings) {
            boundaries.add(building[0]);
            boundaries.add(building[1]);
        }
        Collections.sort(boundaries);

        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        int n = buildings.length, idx = 0;
        for (int boundary : boundaries) {
            while (idx < n && buildings[idx][0] <= boundary) {
                pq.offer(new int[]{buildings[idx][1], buildings[idx][2]});
                idx++;
            }
            while (!pq.isEmpty() && pq.peek()[0] <= boundary) {
                pq.poll();
            }

            int maxn = pq.isEmpty() ? 0 : pq.peek()[1];
            if (ret.size() == 0 || maxn != ret.get(ret.size() - 1).get(1)) {
                ret.add(Arrays.asList(boundary, maxn));
            }
        }
        return ret;
    }
}