面试|详细理解优先队列DelayedWorkQueue

DelayedWorkQueue优先队列

该队列是定制的优先级队列，只能用来存储RunnableScheduledFutures任务。堆是实现优先级队列的最佳选择，而该队列正好是基于堆数据结构的实现。

1.关于堆的一些知识

堆结构是用数组实现的二叉树，数组下标可以表明元素节点的位置，所以省去指针的内存消耗；堆内元素节点的位置取决于节点的某一个属性的大小值，根据父节点是否大于左右节点分为最小堆和最大堆。即二叉树根节点最小则为最小堆，二叉树根节点最大则为最大堆；下面是最小堆和最大堆的示例：

最小堆中，父节点都小于左右节点；其数组形式：[1, 5, 8, 6, 10, 11, 20]

最大堆总，父节点都大于左右节点；其数组形式：[20, 10, 15, 6, 9, 10, 12]

2.堆的一些属性

• 堆都是满二叉树.因为满二叉树会充分利用数组的内存空间；
• 最小堆是指父节点比左节点和右节点都小的结构,所以整个最小堆中,根节点是最小的节点；
• 最大堆是指父节点比左节点和右节点都大的结构,所以整个最大堆中,根节点是最大的节点；
• 最大堆和最小堆的左节点和右节点没有关系,只能判断父节点和左右两节点的大小关系；

基于堆的这些属性，堆适用于找到集合中的最大或者最小值；另外，堆结构记录任务及其索引的关系，便于插入数据或者删除数据后重新排序，所以堆适用于优先队列。

3.堆和数组

堆结构是二叉树，节点实际存储在数组中。如果i是节点的索引，那么就可以用下面的公式计算父节点和子节点在数组中的位置：

// 父节点
parent(i) =floor( (i – 1) / 2);
// 左节点
left(i) = 2 * i + 1;
// 右节点
right(i) = 2 * i + 2;

左节点和右节点在数组中永远是相邻的.例如上面的最小堆，数组为：[1, 5, 8, 6, 10, 11, 20]，数组中的元素在满二叉树中就是从上到下从左到右分布着。

节点属性值	节点索引i	节点父节点 floor( (i – 1) / 2)	节点左节点2 * i + 1	节点右节点2 * i + 2
1	0	-1	1	2
5	1	0	3	4
8	2	0	5	6
6	3	1	-	-
10	4	1	-	-
11	5	2	-	-
20	6	2	-	-

4.堆的插入和移除

堆元素的插入siftUp操作和移除siftDown操作。
比如在最小堆[1, 5, 8, 6, 10, 11, 20]中再插入一个元素4，下面用图示分析插入的过程：
插入之前的二叉树结构：

插入元素4首先放置在数组末尾，也就是二叉树的末尾：

插入元素4（索引为7），首先与其父类（元素为6,索引为3）比较大小，如果是最小堆则交换其与父类的位置，如果是最大堆则不用交换直接结束。我们这里是最小堆，4比6小，所以需要交换其与父类的位置：

交换后如上图所示，找到此时元素4（索引为3）的父类（元素为5，索引为1），比较两者的元素大小，4小于5，所以交换两者的位置：

交换后如上图所示，找到此时元素4（索引为1）的父类（元素为1，索引为0），比较两者的元素大小，4大于1，所以不需要交换。此时确定插入元素4的索引为1的位置。插入的二叉树如图所示：

插入后最小堆的数组形式：[1,4,8,5,10,11,20,6]

整个插入的过程就是一个不断循环比较的过程，通过比较插入元素与父节点元素的大小，最小堆则把较小的元素放置在父节点处，最大堆则把较大的元素放置在父节点处，直到确认插入元素的节点位置。可以看出，每插入一个元素都会对堆进行重排序，且每次排序都是二分排序，所以时间复杂度为logn。

在最大堆[20, 10, 15, 6, 9, 10, 12]中移除元素后，下面用图示分析重排的过程：
最大堆原始二叉树结构：

移除堆的根节点（元素值为20，索引为0）后，取二叉树的最后一个节点，即数组中的最后一个元素12（二叉树中索引为6）放入根节点位置：

需要对新二叉树进行重排序；首先获取根节点的左、右节点，然后比较其大小（最大堆找到较大的节点，最小堆找到较小的节点），我们这里是最大堆，所以比较左节点10和右节点15的大小，找到较大的右节点，并比较右节点（元素为15，索引为2）与根节点（元素为12，索引为0）的大小，把较大的元素放入根节点（最小堆是把较小的元素放入根节点）,交换后的二叉树图为：

重复上面的步骤，比较元素12（索引为2）与其左节点（元素为10，索引为5）的大小，把较大的元素放置在父节点上。最后的二叉树图为：

移除根节点后最大堆的数组形式：[15,10,12,6,9,10]

从堆中获取节点都是默认获取根节点，因为根节点是整个队列中最大或者最小的元素。获取后，需要对队列重排寻找新的根节点元素。重排的顺序跟新增后重排的顺序相反，它是从根节点往下重排，最大堆则把较大元素放置在父节点上，最小堆则把较小元素放置在父节点上；它的时间复杂度同样为logn。

5.DelayedWorkQueue

DelayedWorkQueue是基于堆结构的等待队列。

5.1 类的重要属性

// 数组的初始容量为16 设置为16的原因跟hashmap中数组容量为16的原因一样
private static final int INITIAL_CAPACITY = 16;
// 用于记录RunableScheduledFuture任务的数组
private RunnableScheduledFuture<?>[] queue =
            new RunnableScheduledFuture<?>[INITIAL_CAPACITY];
private final ReentrantLock lock = new ReentrantLock();
// 当前队列中任务数,即队列深度
private int size = 0;
// leader线程用于等待队列头部任务,
private Thread leader = null;
// 当线程成为leader时,通知其他线程等待
private final Condition available = lock.newCondition();

延迟队列是基于数组实现的，初始容量为16；获取延迟队列中头部节点的线程称为leader，说明leader线程是不断变化的，但leader线程在等待，则其他线程也会等待，直到leader线程获取根节点，且从等待线程中产生新的leader线程。

5.2 新增元素到DelayedWorkQueue

1) offer(Runnable)-新增元素

给外界提供一个插入元素的方法.

public boolean offer(Runnable x) {
    if (x == null)
        throw new NullPointerException();
	// 只能存放RunnableScheduledFuture任务
    RunnableScheduledFuture<?> e = (RunnableScheduledFuture<?>)x;
    // 为了保证队列的线程安全,offer()方法为线程安全方法
	final ReentrantLock lock = this.lock;
    lock.lock();
	try {
	// 当前队列实际深度,即队列中任务个数
        int i = size;
		// 如果任务数已经超过数组长度,则扩容为原来的1.5倍
        if (i >= queue.length)
            grow();
		// 队列实际深度+1
        size = i + 1;
		// 如果是空队列 新增任务插入到数组头部;
        if (i == 0) {
            queue[0] = e;
			// 设置该任务在堆中的索引,便于后续取消或者删除任务;免于查找
            setIndex(e, 0);
        } else {
			// 如果不是空队列 则调用siftUp()插入任务
            siftUp(i, e);
        }
		// 如果作为首个任务插入到数组头部
        if (queue[0] == e) {
			// 置空当前leader线程
            leader = null;
			// 唤醒一个等待的线程 使其成为leader线程
            available.signal();
        }
    } finally {
        lock.unlock();
    }
    return true;
}

这个方法理解的难点在于leader线程。若新增任务插入空队列中，首先清空leader线程，并唤醒等待线程中的某一个线程，把唤醒的线程作为leader线程；若新增任务插入前，队列中已经存在任务，则说明已经有leader线程在等待获取根节点，此时无需设置leader线程。leader线程的作用就是用来监听队列的根节点任务，如果leader线程没有获取到根节点任务则通知其他线程等待，这表明leader线程决定着等待线程的状态。
用leader-before这种机制，可以减少线程的等待时间，而每一个等待的线程都有可能成为leader线程。注意：这里还不太清除哪些线程会等待。

2) grow()-数组动态扩容

任务数超过数组长度，则执行扩容.

private void grow() {
	// 当前数组的深度
	int oldCapacity = queue.length;
	// 在原来的基础上,扩大1.5倍,注意每次扩的大小不一样
	int newCapacity = oldCapacity + (oldCapacity >> 1); // grow 50%
	// 如果溢出则取Integer的最大值2^31-1
    if (newCapacity < 0) // overflow
        newCapacity = Integer.MAX_VALUE;
	// 新建长度为newCapacity的数组,并把旧queue数组copy到新数组中
    queue = Arrays.copyOf(queue, newCapacity);
}

延迟队列中的数组支持动态扩容，可以理解为延迟队列的容量接近无穷大，即该队列适用放置那种短期的任务。

3) siftUp(int,RunnableScheduledFuture)-新增任务后重排

新增任务插入队列(数组)，首先插入到数组的尾部，然后对比其与该位置的父节点的大小，如果新增任务大于父节点任务（此处是最小堆），则新增任务位置不变，否则改变其与父节点的位置，并再比较父节点与父父节点的大小，直到根节点。插入的过程可以结合上面堆的二叉树变化过程图一起理解。
插入流程图：

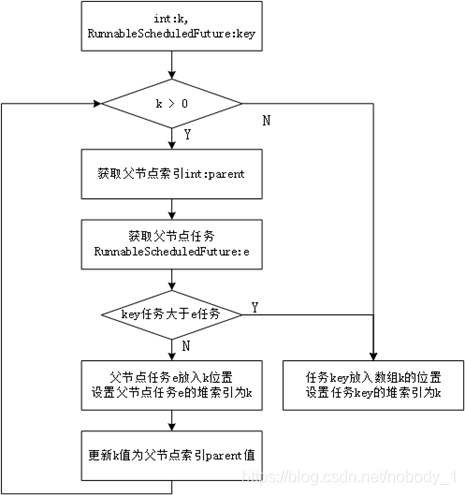
private void siftUp(int k, RunnableScheduledFuture<?> key) {
	// 循环,当k为根节点时结束循环
	while (k > 0) {
		// 获取k的父节点索引,相当于(k-1)/2
        int parent = (k - 1) >>> 1;
		// 获取父节点位置的任务
        RunnableScheduledFuture<?> e = queue[parent];
		// 判断key任务与父节点任务time属性的大小,即延迟时间
        if (key.compareTo(e) >= 0)
            break; // 父节点任务延迟时间小于key任务延迟时间,则退出循环
        // 否则交换父节点parent与节点k的任务
		queue[k] = e;
		// 更新任务e在堆中的索引值
        setIndex(e, k);
		// 更新k的值 比较其与父父节点的大小
        k = parent;
	}
	// 任务key放入数组k的位置,k的值是不断更新的
	queue[k] = key;
	// 设置任务key在堆中的索引值
    setIndex(key, k);
}

这里compareTo()方法在ScheduledFutureTask类中有定义，本质上是比较任务的time属性大小，即延迟时间的长短。我们后面分析ScheduledFutureTask类的时候会学习到。

4) put(Runnable)/add(Runnable)/offer(Runnable,long,TimeUnit)

这三个方法的作用都是往队列中添加元素.

public void put(Runnable e) {
offer(e);
}

public boolean add(Runnable e) {
    return offer(e);
}

public boolean offer(Runnable e, long timeout, TimeUnit unit) {
    return offer(e);
}

可以看到，三个方法调用的都是同一个方法offer(Runnable)；即使第三个方法offer()传递超时时间，该时间也被忽略掉，表明过来的任务不会因为超时而丢弃，反而都会放入延迟队列中。另外，上面分析过offer(Runnable)方法，过来的任务不会因为队列满而拒绝任务，反而队列的大小接近Integer.MAX_VALUE，能保证任务放入成功。由于队列的这个特性，使得线程池ScheduledThreadPoolExecutor的最大线程数也设置为Integer.MAX_VALUE。

5.3 移除元素

1) poll()-获取队列根节点

public RunnableScheduledFuture<?> poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();
	try {
		// 获取队列根节点,即延迟时间最小,优先级最高的任务
        RunnableScheduledFuture<?> first = queue[0];
		// 如果根节点为null 或者节点延迟还没到 则返回null
        if (first == null || first.getDelay(NANOSECONDS) > 0)
            return null;
        else
			// 否则执行finishPoll()方法
            return finishPoll(first);
    } finally {
        lock.unlock();
    }
}

获取根节点元素后，需要对队列重新排序.具体看finishPoll(RunnableScheduledFuture)方法的分析。该方法获取队列根节点，可能返回任务，也可能返回null。

2) finishPoll(RunnableScheduledFuture)-获取根节点后重排序

private RunnableScheduledFuture<?> finishPoll(RunnableScheduledFuture<?> f) {
	// 因为取出根节点 所以队列深度减1 并赋值给s
    int s = --size;
	// 获取队列最后一个任务
    RunnableScheduledFuture<?> x = queue[s];
	queue[s] = null; // 该位置元素置空
	// 如果s已经根节点则直接返回，否则堆重排序
    if (s != 0)
        siftDown(0, x);
	// 取出来的任务 设置其堆索引为-1
    setIndex(f, -1);
    return f; // 返回任务
}

3) siftDown(int,RunnableScheduledFuture)-移除元素后重排序

private void siftDown(int k, RunnableScheduledFuture<?> key) {
	// 取队列当前深度的一半 相当于size / 2
    int half = size >>> 1;
    // 索引k(初值为0)的值大于half时 退出循环
    while (k < half) {
	// 获取左节点的索引
        int child = (k << 1) + 1;
		// 获取左节点的任务
        RunnableScheduledFuture<?> c = queue[child];
		// 获取右节点的索引
        int right = child + 1;
		// 如果右节点在范围内 且 左节点大于右节点,
        if (right < size && c.compareTo(queue[right]) > 0)
			// 更新child的值为右节点索引值 且更新c为右节点的任务
            c = queue[child = right];
		// 如果任务key小于任务c 则退出循环(最小堆)
        if (key.compareTo(c) <= 0)
            break;
		// 否则把任务c放到k上(较小的任务放到父节点上)
        queue[k] = c;
		// 设置任务c的堆索引
        setIndex(c, k);
		// 更新k的值为child
        k = child;
    }
    // 任务key插入k的位置
    queue[k] = key;
    // 设置任务key的堆索引k
    setIndex(key, k);
}

执行的流程图为：

4) take()-等待获取根节点

public RunnableScheduledFuture<?> take() throws InterruptedException {
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
	    // 自循环，实现对队列的监控 保证返回根节点
        for (;;) {
			// 获取根节点任务
            RunnableScheduledFuture<?> first = queue[0];
			// 如果队列为空，则通知其他线程等待
            if (first == null)
                available.await();
            else {
				// 获取根节点任务等待时间与系统时间的差值
                long delay = first.getDelay(NANOSECONDS);
				// 如果等待时间已经到，则返回根节点任务并重排序队列
                if (delay <= 0)
                    return finishPoll(first);
				// 如果等待时间还没有到,则继续等待且不拥有任务的引用
                first = null; // don't retain ref while waiting
				// 如果此时等待根节点的leader线程不为空则通知其他线程继续等待
                if (leader != null)
                    available.await();
                else {
					// 如果此时leader线程为空,则把当前线程置为leader
                    Thread thisThread = Thread.currentThread();
                    leader = thisThread;
                    try {
						// 当前线程等待延迟的时间
                        available.awaitNanos(delay); 
                    } finally {
						// 延迟时间已到 则把当前线程变成非leader线程
						// 当前线程继续用于执行for循环的逻辑
                        if (leader == thisThread)
                            leader = null;
                    }
                }
            }
        }
} finally {
	// 如果leader为null 则唤醒一个线程成为leader
        if (leader == null && queue[0] != null)
            available.signal();
        lock.unlock();
    }
}

此方法势必会返回根节点的任务，常用于从队列中循环获取任务。

5) poll(long,TimeUnit)-超时等待获取根节点

允许等待超时，其他过程同poll()方法的注释.

public RunnableScheduledFuture<?> poll(long timeout, TimeUnit unit) throws InterruptedException {
    long nanos = unit.toNanos(timeout);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        for (;;) {
            RunnableScheduledFuture<?> first = queue[0];
            if (first == null) {
                if (nanos <= 0)
                    return null;
                else
                    nanos = available.awaitNanos(nanos);
            } else {
                long delay = first.getDelay(NANOSECONDS);
                if (delay <= 0)
                    return finishPoll(first);
                if (nanos <= 0)
                    return null;
                first = null; // don't retain ref while waiting
                if (nanos < delay || leader != null)
                    nanos = available.awaitNanos(nanos);
                else {
                    Thread thisThread = Thread.currentThread();
                    leader = thisThread;
                    try {
                        long timeLeft = available.awaitNanos(delay);
                        nanos -= delay - timeLeft;
                    } finally {
                        if (leader == thisThread)
                            leader = null;
                    }
                }
            }
        }
    } finally {
        if (leader == null && queue[0] != null)
            available.signal();
        lock.unlock();
    }
}

6) peek()-直接返回根节点

public RunnableScheduledFuture<?> peek() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return queue[0];
    } finally {
        lock.unlock();
    }
}

peek()方法会立即返回根节点任务，而忽略延迟时间。

7) remove(Object)-删除任务

public boolean remove(Object x) {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
	    // 获取任务x的heapIndex
        int i = indexOf(x);
		// 如果为-1 则表明不在队列内
        if (i < 0)
            return false;

		// 设置删除任务的heapIndex为-1
        setIndex(queue[i], -1);
		// 队列深度-1
        int s = --size;
		// 获取队列末尾的节点任务
        RunnableScheduledFuture<?> replacement = queue[s];
        queue[s] = null;
		// 如果删除的任务节点不是末尾的节点,则重排序
        if (s != i) {
            siftDown(i, replacement);
            if (queue[i] == replacement)
                siftUp(i, replacement);
        }
        return true;
    } finally {
        lock.unlock();
    }
}

6.总结

本篇围绕ScheduledThreadPoolExecutor类的延迟队列DelayedWorkQueue展开分析，着重分析堆数据结构以及DelayedWorkQueue队列的方法。