量子人工智能：从量子信息表征到可训练混合模型的系统综述

在经典人工智能快速扩张的同时，计算范式本身也在发生变化：一方面，现代深度学习依赖大规模算力与数据，训练与推理的成本持续攀升，模型能力与硬件能效之间的张力越来越明显；另一方面，量子计算以“量子态空间指数维度”和“相位干涉”作为核心资源，被寄予在特定任务上突破经典计算瓶颈的期待。把这两股力量放在同一张图谱里，会出现一个看似直观、实则极其复杂的问题：量子计算究竟能在“学习”意义上带来什么，哪些收益是物理可实现且可验证的，哪些又只是表述层面的想象。对这一问题做严肃讨论，必须把“算法可能性”“数据进入量子态的代价”“噪声与有限测量带来的统计误差”“可训练性与泛化性”等议题放在同一套理论框架里，而不是停留在“量子就是更强”的泛泛叙述。围绕这一点，量子机器学习与量子人工智能在过去数年形成了相对清晰的学术脉络：既有对量子计算如何嵌入经典学习流程的工程化探索，也有对学习理论、复杂度边界、以及量子优势判据的系统反思。典型综述工作强调：量子学习潜在优势往往建立在若干前提上，例如数据加载模型、可实现的电路深度、以及与最强经典基线的对照方式。任何脱离这些前提的“优势陈述”，都很难在科学意义上成立。

如果把“量子人工智能”当作一门交叉学科，它并不等同于“在量子计算机上跑神经网络”，也不等同于“用AI预测量子材料性质”。更贴近学术共同体的理解是：在量子信息处理的约束下重新审视学习问题，既包括用量子资源构造新的表示、核函数或生成机制（常被概括为 Quantum-for-AI），也包括用机器学习与智能优化方法改进量子系统的控制、校准、纠错与误差缓解（常被概括为 AI-for-Quantum）。这种双向结构意味着，本文的综述不把重点放在遥远的“未来应用想象”，而是把篇幅集中在理论层面的可验证对象：模型形式、训练目标、梯度估计、噪声模型、复杂度与样本复杂度、以及围绕“量子优势”可落地的评测方法。这样做的目的很直接：让读者能够把量子人工智能当作一套可以推导、可以实验对照、可以被证伪或证实的技术体系来理解，而不是一组松散的概念标签。

图1 量子人工智能研究图谱：两条主线与三层技术栈

2 综述框架：概念边界、问题结构与方法论

2.1 概念边界：量子人工智能不只是“量子版深度学习”

在讨论“量子人工智能”时，一个常见陷阱是把它理解成“把经典深度网络的每一层都换成量子电路”。这种直觉在形式上容易成立，因为量子电路本身可以被参数化，并通过测量输出实数，从而与经典损失函数连接，形成可训练系统。然而，量子系统与经典系统的差异并不体现在“是否可训练”这一点上，而体现在训练的资源模型：量子电路输出不是直接可得的确定性数值，而是由测量采样得到的统计估计；电路运行受到噪声、退相干与门保真度限制；更重要的是，经典数据进入量子态的过程本身可能消耗与数据维度相关的大量门操作，这会抵消任何后续的量子加速。正是因为这些结构性差异，量子学习研究逐渐从“把模型搬过去”转向“重新组织学习问题”，强调在何种输入模型、何种硬件约束下，哪些学习任务存在可证明或可观察的优势空间。

同时也必须指出，量子人工智能并非只有“在量子计算机上做机器学习”这一条路。另一条同样重要的路线是用机器学习服务量子技术本身：用强化学习或贝叶斯优化去做量子门校准与脉冲控制，用神经网络或图模型去做表面码的综合征解码，用回归模型去学习噪声漂移并指导误差缓解策略。这条路线的理论价值在于，它把“量子系统的难点”形式化为可优化或可学习的目标函数，从而把量子工程问题映射成机器学习问题，并在真实设备上获得可量化的收益（例如更低的逻辑错误率、更短的实时解码延迟、更高的保真度）。

2.2 两条主线与三层技术栈：把“能跑”与“能学”放在同一张图里

为了避免综述变成“名词百科”，更有效的方式是把量子人工智能拆成可分析的结构。一个实用的组织方法是：横向用“两条主线”刻画研究目标，纵向用“三层技术栈”刻画实现路径。横向的 Quantum-for-AI 关注“量子资源是否能改写学习的计算结构”，例如通过量子特征映射构造难以经典模拟的核函数，或通过量子采样机制生成具有特定统计结构的数据分布；AI-for-Quantum 关注“学习算法是否能把量子硬件的复杂性吸收掉”，例如把校准、控制、纠错、编译、误差缓解变成可学习的策略或模型。纵向的三层栈则从下到上依次是：硬件与噪声（决定可执行电路的深度与误差结构）、系统与编译（决定你能否把算法映射到特定拓扑并降低开销）、算法与学习理论（决定模型表达能力、训练可行性与泛化边界）。把横向与纵向交叉起来，你会发现很多争议都能被定位：某个“优势”到底卡在数据加载、卡在噪声、还是卡在训练景观与泛化理论上。

表1给出这种组织方式的一个对照视角，它不是为了把内容做成清单，而是为了在后续长段落讨论中保持“结构对齐”，让读者知道每一段理论讨论在整套框架中处于哪一层、服务哪一条主线。

表1 量子人工智能的“两条主线—三层技术栈”结构对照（概念化归纳）

主线/技术栈	硬件与噪声层	系统与编译层	算法与学习理论层
Quantum-for-AI	NISQ噪声下电路深度可行域；采样次数与统计误差	特征映射电路的编译与拓扑适配；测量分组与并行化	量子核/变分模型的表达与泛化；量子优势判据
AI-for-Quantum	漂移噪声建模；门校准与脉冲控制	编译与路由策略学习；噪声感知映射	解码器学习；误差缓解学习；策略优化与样本效率

2.3 学习问题的“共同骨架”：表示、目标、优化、复杂度

不论是量子核还是变分量子模型，不论是解码器还是控制策略，几乎所有量子人工智能工作都绕不开四个骨架性问题。第一是表示：输入如何映射到模型内部状态，尤其在量子侧需要明确“编码电路”的形式与代价。第二是目标：模型要优化的到底是什么，是经验风险、能量期望、还是逻辑错误率等工程指标。第三是优化：梯度如何估计，优化景观是否存在平坦化问题，噪声与有限采样如何影响收敛。第四是复杂度：在给定的输入模型下，训练或推断的时间复杂度、样本复杂度是否真的优于最佳经典算法。许多对量子AI的误解来自于只讨论其中一个骨架，比如只谈“量子态空间指数维度”而不谈“测量采样导致的方差”，或只谈“量子特征映射很复杂”而不谈“经典核方法同样可以在高维特征空间工作”。成熟的综述往往强调：量子优势需要在完整骨架下被评估，而不是用单一指标替代。

3 理论知识与技术基础

3.1 量子态、张量积与测量：学习模型的“状态空间”从哪里来

理解量子人工智能，首先要把“量子态”当作一种信息表示结构来掌握，而不仅仅是物理概念。在门模型量子计算中，n个量子比特构成的纯态可以写成计算基上的叠加，这一点是许多“指数维度直觉”的来源。更重要的是，这个表示并不是在计算机里以显式向量存在，而是通过电路制备并通过测量采样来访问。对于学习而言，这意味着模型的内部表示天然带着“不可完全读取”的约束：你不能像在经典网络里那样随时取出隐藏层向量，而必须通过设计测量算符来间接获得期望值或概率分布。

$$
|\psi\rangle=\sum_{z\in{0,1}^n}\alpha_z|z\rangle,\quad \sum_z|\alpha_z|^2=1
$$

当你对态进行计算基测量，得到比特串 z 的概率由 Born 规则给出：

$$
p(z)=|\langle z|\psi\rangle|^2
$$

从学习视角看，这个概率分布可以被理解成模型的输出分布之一；而“训练”往往就是通过调节电路参数，使得某个由测量定义的损失函数最小。注意这里的核心不是“量子态能表示很多数”，而是“你只能通过采样获得关于这些数的统计信息”，这会直接引出测量次数与方差控制的问题，后文在训练与泛化部分会反复出现。

当系统处于噪声环境时，纯态描述往往不再成立，需要使用密度矩阵。密度矩阵的好处是，它把“经典不确定性”与“量子混合”都统一在一个算子对象里，使得噪声演化可以用量子信道表示。在量子人工智能里，密度矩阵并不是为了更“高深”，而是为了把噪声引入学习模型：你的输出期望值不再来自一个理想的纯态，而来自噪声信道作用后的状态。这样，训练过程中的损失函数不仅依赖参数，也依赖噪声模型。

$$
\rho=\sum_i p_i|\psi_i\rangle\langle\psi_i|,\quad p_i\ge 0,\ \sum_i p_i=1
$$

3.2 量子门电路与参数化：把“可学习性”嵌入幺正演化

门模型量子计算的演化由幺正算子描述，电路是幺正算子的分解。量子AI常用的“可训练量子模型”通常采用参数化量子电路（Parameterized Quantum Circuit, PQC）：在电路中引入可调角度的旋转门或更一般的连续参数门，然后把输出定义为某个可观测量的期望值。这样做的关键在于：期望值对参数是可微的（至少在一定条件下），从而可以与经典优化器耦合，形成混合优化闭环。之所以大量工作选择混合结构，是因为纯量子端做全局优化在 NISQ 条件下不可行，而混合结构把“搜索与更新”交给经典计算，把“难以经典模拟的态制备与测量”交给量子硬件，从而在资源上折中。变分混合算法的理论化讨论从早期就强调这种分工哲学：量子端负责在态空间里提供表达能力，经典端负责利用成熟的优化工具处理参数更新。

3.3 噪声、量子信道与 Kraus 表示：为什么“同一个模型”在真实设备上会变形

量子人工智能不能回避噪声，因为噪声不是“实现细节”，而是直接改变学习目标的算子。一个通用表述是用 Kraus 算子刻画量子信道：任何完全正、迹保持的量子信道都可以写成若干 Kraus 算子作用的和。这样，电路中每一层门的噪声都可以组合成整体信道，最终影响测量得到的分布或期望值。

$$
\rho'=\sum_k E_k\rho E_k^\dagger,\quad \sum_k E_k^\dagger E_k=I
$$

在学习语境下，这意味着两个后果。第一，损失函数变成“含噪期望”的函数，哪怕参数不变，噪声强度变化也会让模型输出漂移。第二，噪声与有限采样叠加，往往会导致梯度估计方差增大，训练更不稳定。因此，量子AI里大量技巧（误差缓解、噪声感知编译、鲁棒优化）都可以理解为“把信道效应吸收到训练过程里”，而不是事后补丁。NISQ 时代的系统性综述通常把噪声作为核心约束来讨论可行算法族。

3.4 经典学习的风险最小化视角：把量子模型放进同一套统计框架

从统计学习角度，训练可以视为经验风险最小化：在样本集上最小化损失的平均值，并通过正则项或结构约束控制泛化。量子模型并不会改变这个宏观结构，它改变的是模型族 f(x;θ) 的实现方式以及梯度/输出的获取方式。把这一点说清楚很重要，因为它能把许多“量子AI的新概念”翻译成经典学习语言：量子特征映射对应一个隐式特征空间，量子测量对应某种读出函数，变分电路对应一种参数化假设空间，测量次数对应统计估计的样本数（shots）。当我们用统一的风险最小化公式表示时，量子与经典的差异主要进入到 f 的可计算性、以及对 f 的评估代价中。

$$
\min_\theta \frac{1}{N}\sum_{i=1}^N \ell\big(f(x_i;\theta),y_i\big)+\lambda,\Omega(\theta)
$$

3.5 “量子优势”需要被精确定义：输入模型、对照基线与可验证性

量子优势在量子AI语境中常被过度泛化。更严谨的做法是把优势拆成三层：计算复杂度优势（时间或查询复杂度的可证明分离）、样本复杂度优势（学习所需样本量的量级差异）、以及实际运行时优势（在真实硬件与系统软件栈上端到端更快或更准）。其中第一层往往依赖对输入访问方式的假设，例如数据是否以量子态形式给定，是否允许 QRAM 等；第二层需要学习理论的可证明界；第三层需要严格的基准与工程实现。经典视角的量子学习综述反复强调：如果输入模型过于理想化，复杂度优势可能并不转化为实际优势；而如果对照基线不够强，所谓“优势”可能只是实现差异。

4 量子机器学习的核心范式：编码、可观测、训练与可训练性

4.1 数据如何进入量子模型：编码电路不是“免费入口”

量子AI的第一道门槛不是量子电路多复杂，而是经典数据如何被编码到量子态。所谓编码（embedding/encoding）通常指构造一个与输入 x 相关的量子电路 Uφ(x)，作用在初态 |0…0⟩ 上得到 |φ(x)⟩。不同编码方式的差异体现在两个层面：一是表达能力，即 |φ(x)⟩ 在态空间里能否区分不同输入；二是代价，即构造 Uφ(x) 需要多少门深度与多少控制参数。很多“理论量子加速”在这里就会遇到现实对冲：如果编码电路深度与输入维度线性甚至更高增长，而硬件允许的深度又非常有限，那么后续任何复杂量子处理都很难执行。

常见编码包括角度编码、幅度编码、基态编码等。角度编码通常把每个特征映射到若干旋转门角度，电路深度相对可控，但需要更多量子比特或重复层数才能表达复杂相关性；幅度编码理论上能在 n 个量子比特上表示 2^n 维向量，但制备任意幅度态一般需要复杂电路或额外的输入模型假设。对这些编码方式的讨论并不应该停留在“谁更强”，而应该落到学习任务的结构上：如果数据本身具有低秩、稀疏或可生成结构，编码电路可以利用结构降成本；如果数据没有可利用结构，编码可能成为优势的主要瓶颈。经典视角的综述对这一点给出过系统讨论，并提醒读者关注“数据加载代价”在总复杂度中的占比。

4.2 量子特征映射与量子核：把“不可模拟性”转化为学习优势并不自动成立

量子核方法是量子AI里最具有“理论可对照性”的路线之一，因为它把量子部分压缩成一个可验证对象：核函数 k(x,x')。给定特征映射电路 Uφ(x)，可以定义量子态 |φ(x)⟩=Uφ(x)|0⟩，然后核函数可以由态重叠定义，例如用保真度或其变体作为核值。一个常见定义是：

$$
k(x,x')=\left|\langle 0|U_\phi(x)^\dagger U_\phi(x')|0\rangle\right|^2
$$

这个公式的重要性在于，它把量子电路的复杂性“封装”进核估计过程，而后续的学习（例如 SVM、核岭回归）可以用经典凸优化完成。这样，训练稳定性与可解释性往往更好。然而，量子核方法的难点也很明确：核值的估计来自测量采样，误差受 shots 限制；更关键的是，即使核在计算上难以经典模拟，也不意味着它对某个数据分布就是“好核”。有工作专门指出，“不可模拟性”是获得优势的必要条件但非充分条件，因为某些核可能在统计上并不区分标签结构，从而即使你能高效估计，也无法提升泛化性能。

从学习理论角度，核方法的泛化能力与核矩阵的谱性质、margin 等有关。量子核的研究因此自然分成两条：一条研究怎样设计 Uφ(x) 让核在统计上有效，另一条研究在什么输入模型下估计核比经典更快。把这两条合起来，才可能形成真正的端到端优势陈述。这也是为什么近年来的量子核研究越来越强调“数据分布—特征映射—核谱结构”的耦合分析，而不是只展示电路复杂度。

4.3 变分量子模型：可训练电路如何输出“可优化的实数”

变分量子模型把量子电路看作可训练模型的一部分。典型结构是：先用数据编码电路把 x 写入量子态，再用含参数 θ 的可训练电路 U(θ) 进行演化，然后测量某个可观测量 O 的期望作为输出。形式上可以写成：

$$
\hat{y}(x;\theta)=\langle 0|U_\phi(x)^\dagger U(\theta)^\dagger,O,U(\theta)U_\phi(x)|0\rangle
$$

这个表达式与经典神经网络的差异并不在于“是否是函数逼近器”，而在于输出的获取方式：你得到的是期望值的统计估计。于是训练的每一步都涉及“测量次数—方差—优化器稳定性”的折中。变分模型之所以在 NISQ 时代被广泛研究，是因为它对相干时间要求相对较低，并且能够与经典优化器形成闭环，这一点在变分混合算法理论中被系统讨论。

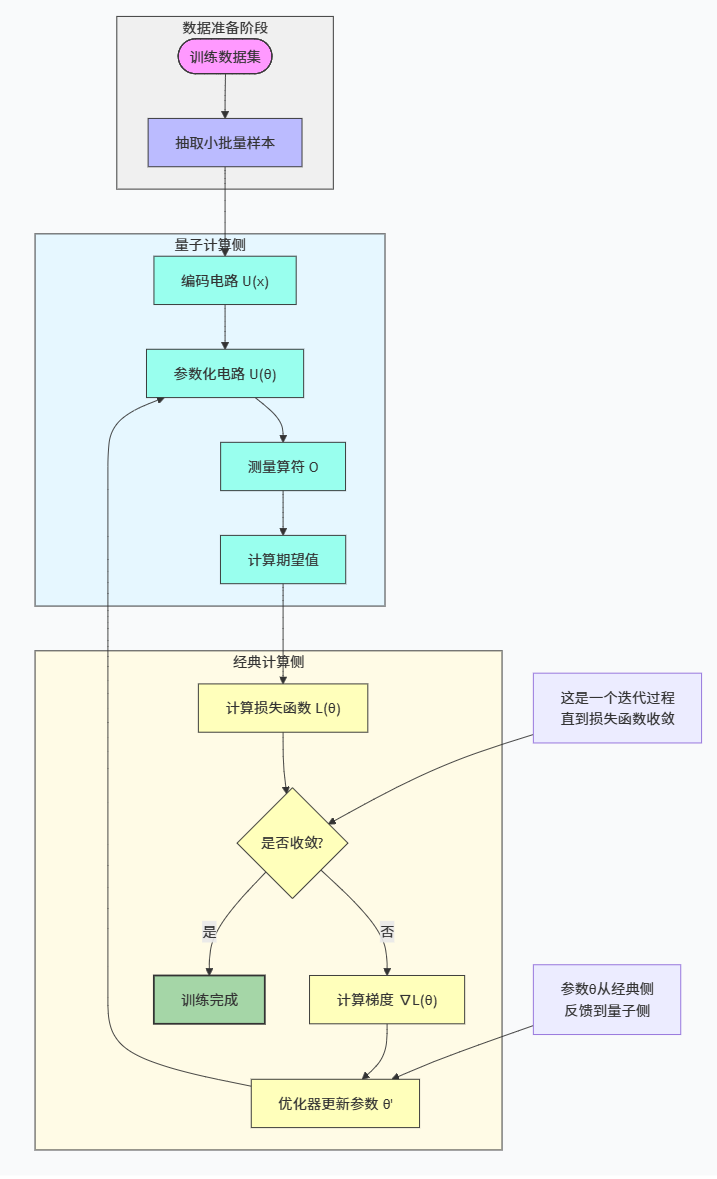
图2 量子-经典混合训练闭环流程图

4.4 梯度如何在量子硬件上得到：参数偏移法则与可微量子编程

在经典深度学习里，反向传播使得梯度计算几乎“免费”地嵌入训练流程；在量子电路里，梯度必须通过额外的电路评估获得。参数偏移法则（parameter-shift rule）是最常用的途径之一：当某些参数门满足特定谱条件时，期望值对参数的导数可以由两次移位后的电路期望差来表示。最典型的形式是：

$$
\frac{\partial}{\partial \theta}\langle O\rangle_\theta
=\frac{1}{2}\Big(\langle O\rangle_{\theta+\pi/2}-\langle O\rangle_{\theta-\pi/2}\Big)
$$

这条公式看似简单，却是“可微量子编程”的关键：它把梯度计算转化为可在硬件上执行的两次前向电路评估，从而使得量子电路可以像神经网络层一样被优化。需要注意的是，这里的“2次评估”只是单参数的最理想情况，真实电路可能包含大量参数与多种门类型，梯度评估代价会随参数数目和测量算符复杂度增长，因此系统层面的并行化与测量分组策略同样重要。参数偏移及其推广在相关工作中有系统讨论。

4.5 可训练性：为什么会出现“训练景观荒原”，以及它在量子AI里更尖锐

量子变分模型的一个核心理论问题是可训练性。大量研究发现，在某些电路结构与目标函数下，梯度方差会随系统规模指数衰减，使得随机初始化后几乎看不到有效梯度，训练陷入“平坦高原”，这类现象通常被称为 barren plateaus。更棘手的是，噪声会进一步加剧这种平坦化，因为噪声会把态推向更“混合”的分布，从而减少参数变化对测量期望的敏感性。对量子神经网络训练景观的系统分析指出，这种现象与浓缩测度、随机电路的表达特性等有关，因此缓解策略往往需要从电路结构、初始化策略、目标函数局部性等方面入手，而不是仅仅更换优化器。

从学习角度看，barren plateaus 的意义在于：它把“理论表达能力”与“可实现训练”拉开距离。一个电路即使具备强表达能力，也可能因训练信号消失而无法在有限样本与有限噪声条件下被学到。因此，量子AI里的模型设计经常强调局部结构、问题启发式 ansatz、以及与任务相关的对称性约束，这些做法可以理解为在假设空间中引入“可训练性先验”。这种“带偏置的模型设计”与经典深度学习其实有相通之处，只是量子侧的约束更硬。

5 硬件与系统栈：NISQ 约束下的工程事实与可量化数据

5.1 NISQ 的意义：不是“弱量子计算”，而是“噪声主导的可用量子资源”

NISQ（Noisy Intermediate-Scale Quantum）通常指量子比特规模达到几十到几百、但仍远未达到容错阈值所需误差水平的设备时代。这个概念的重要性不在于给硬件贴标签，而在于它规定了算法与模型必须面对的现实：电路深度受限、噪声不可忽略、测量成本高、可用拓扑有限。NISQ 时代的计算往往无法依赖长深度的相干演化，因此混合变分算法、短深度特征映射、以及误差缓解成为常见策略。对 NISQ 时代的系统性讨论强调：量子优势可能在某些采样类或模拟类任务上先出现，但它并不会自动迁移到所有学习任务。

5.2 主流硬件路线的公开指标：规模、连接性与“能跑什么样的量子AI”

量子AI的理论讨论必须落地到硬件，因为模型训练所需的电路深度、门类型、连通图结构、以及中途测量能力都直接决定“哪些模型是可执行的”。为了把抽象讨论转化为可操作的信息，表2整理了多条硬件路线在公开资料中披露的规模与连接性指标。这里的目标不是做商业对比，而是让读者看到一个事实：不同路线的“量子比特数”并不在同一语义空间里，门模型的“物理量子比特数”与光量子系统的“模式数”、退火系统的“耦合器拓扑”、以及离子阱系统的“全连接特性”在算法映射上差异巨大。理解这种差异，是后续讨论“量子AI算法与硬件适配”不可缺少的基础。

表2 典型量子计算平台公开规格与关键指标（节选，均来自公开资料）

平台/系统（公开节点）	技术路线	公开规模指标	连接性/关键能力（公开描述）	与量子AI相关的直接含义
IBM 量子路线图节点（Eagle/Osprey/Condor 等）	超导门模型	127/433/1121 量子比特等节点	路线图强调可扩展处理器与系统级集成	适合短深度变分与核电路；编译/路由是关键开销来源
Google 表面码阈下实验处理器	超导门模型	72 量子比特实现距离5；105 量子比特实现距离7	集成实时解码；面向表面码运行	容错路径的关键里程碑：实时解码把“学习/推理”引入纠错回路
Quantinuum System Model H2（升级后）	离子阱门模型	从32升级到56物理量子比特	all-to-all 全连接（公开表述）	全连接利于某些变分结构与纠错原语；降低路由复杂度
IonQ Forte（基准论文配置）	离子阱门模型	30 量子比特；通过 AQ 基准到 #AQ 29	all-to-all 操作；应用导向基准	把“能跑算法”量化为 AQ；适合中小规模混合训练与基准对照
Rigetti Ankaa-2	超导门模型	84 量子比特	公布中位两比特门保真度约98%	保真度与深度约束下，误差缓解与噪声感知训练更关键
D-Wave Advantage（商业系统）	量子退火/模拟退火类	5000+ 量子比特；耦合器 35000+	15-way 连接性	更适合组合优化/能量最小化类映射；与学习结合多在混合求解器层
Xanadu Borealis	光量子（玻色采样类）	216 squeezed modes（模式数）	面向玻色采样任务	更偏向采样与生成机制研究；与“量子生成模型”关联更强
Atom Computing（公开报道节点）	中性原子	1180 量子比特（公开报道）	强调全连接/可重构连接（路线特性）	大规模比特潜力对核/采样类模型有吸引力，但需结合可用门集与噪声

数据来源说明：IBM 路线图节点与处理器规模来自 IBM 公开路线图材料。 Google 表面码阈下实验的 72/105 量子比特与距离5/7来自公开论文。 Quantinuum H2 从32升级到56物理量子比特来自官方博客。 IonQ Forte 的 30 量子比特与 #AQ 29 来自基准论文摘要信息。 Rigetti Ankaa-2 的 84 量子比特与两比特门保真度来自公开信息。 D‑Wave Advantage 的 5000+ 量子比特、35000+ 耦合器与 15-way 连接性来自官方资料。 Xanadu Borealis 的 216 模式来自公开论文。 Atom Computing 的 1180 量子比特来自公开报道。

5.3 IBM 处理器节点的时间线：把“规模增长”转化为可绘制数据

量子AI的很多讨论会提到“量子比特数在增长”，但如果不给出可绘制的公开节点数据，这句话就无法支持任何工程判断。IBM 的路线图材料公开了多个处理器节点与量子比特规模，这些节点常被用来讨论超导路线的扩展节奏。表3把路线图中常被引用的节点整理为“年份—节点—量子比特数”的形式，目的不是预测未来，而是为读者提供一组可以用来画图、用来对照“电路深度与拓扑复杂度”的公开数据。需要注意：路线图数据反映的是公开计划与节点命名体系，读者在做工程评估时仍需结合当下可用云端后端的实际指标与校准数据，但路线图节点至少提供了讨论的坐标系。

表3 IBM 公开路线图中的处理器节点与量子比特规模（用于绘图的数据整理）

节点名称（公开）	量子比特数（公开）	公开路线图语境中的定位
Eagle	127	早期大于百比特节点
Osprey	433	数百比特规模节点
Condor	1121	千比特级节点（路线图节点）
Heron	133	后续架构节点（路线图提及）

数据来源：IBM Quantum Roadmap 公开材料。

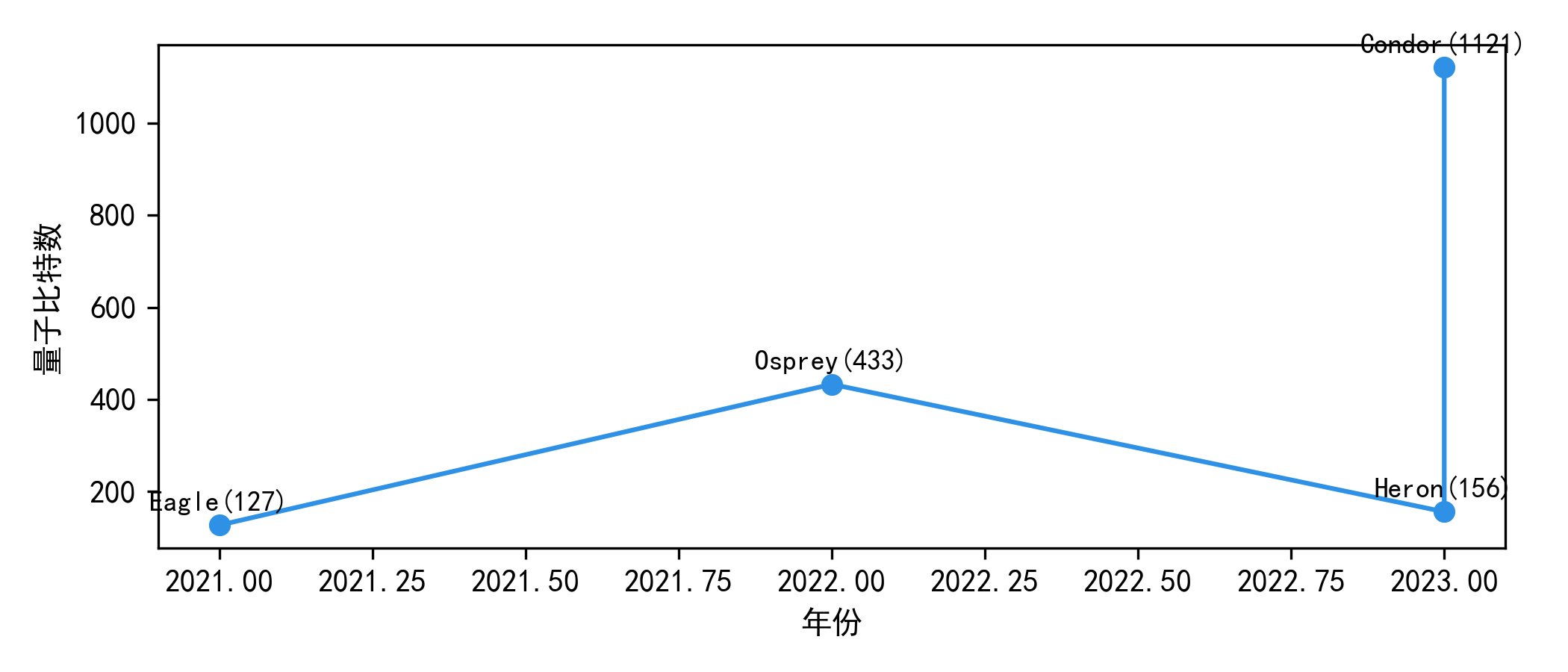
图3 IBM 量子处理器节点量子比特数时间线

5.4 开源软件栈的“真实热度”：用 GitHub 指标把生态讨论数据化

量子AI的另一个常见误区是只谈“算法概念”，忽略工具链成熟度对研究可复现性的影响。开源框架在这里尤其重要：一方面，它们决定了你能否快速搭建混合训练闭环、是否支持自动微分、是否提供噪声模拟与硬件后端；另一方面，它们的社区活跃度也反映了生态对某种范式的偏好。为了满足“真实数据”要求，表4直接整理了多个主流框架在 GitHub 页面公开显示的 stars 与 forks（均为页面展示的近似值），这些数据可以直接用于绘制柱状图，帮助读者建立对生态规模的直观认识。需要强调的是，stars 并不等价于学术价值，但它能作为“工具可用性与传播度”的粗粒度信号，与论文数量、工业投入等维度一起构成更完整的生态判断。

表4 主流量子AI/量子开发框架 GitHub 公开指标（截至页面抓取时显示）

框架	主要定位（公开描述概括）	Stars（约）	Forks（约）	与量子AI相关的关键点
Qiskit	面向量子电路、算符与 primitives 的开源 SDK	6.9k	2.7k	完整工具链与云端生态，适合变分/核/误差缓解实验
Cirq	面向 NISQ 的 Python 框架与硬件建模	4.8k	1.2k	与谷歌生态结合紧密，强调电路与噪声建模
PennyLane	可微量子编程与量子机器学习框架	2.9k	715	强调自动微分与混合训练，QML范式友好
TensorFlow Quantum	面向混合量子-经典 ML 的 TF 框架	2.1k	643	与 TF/Keras 深度集成，适合大规模仿真与混合工作流

数据来源：Qiskit GitHub 页面显示 Star 6.9k、Fork 2.7k。 Cirq 组织页/文件页显示 Star 4.8k、Fork 1.2k。 PennyLane 页面显示 Stars 2.9k、Forks 715。 TensorFlow Quantum 页面显示 Stars 2.1k、Forks 643。

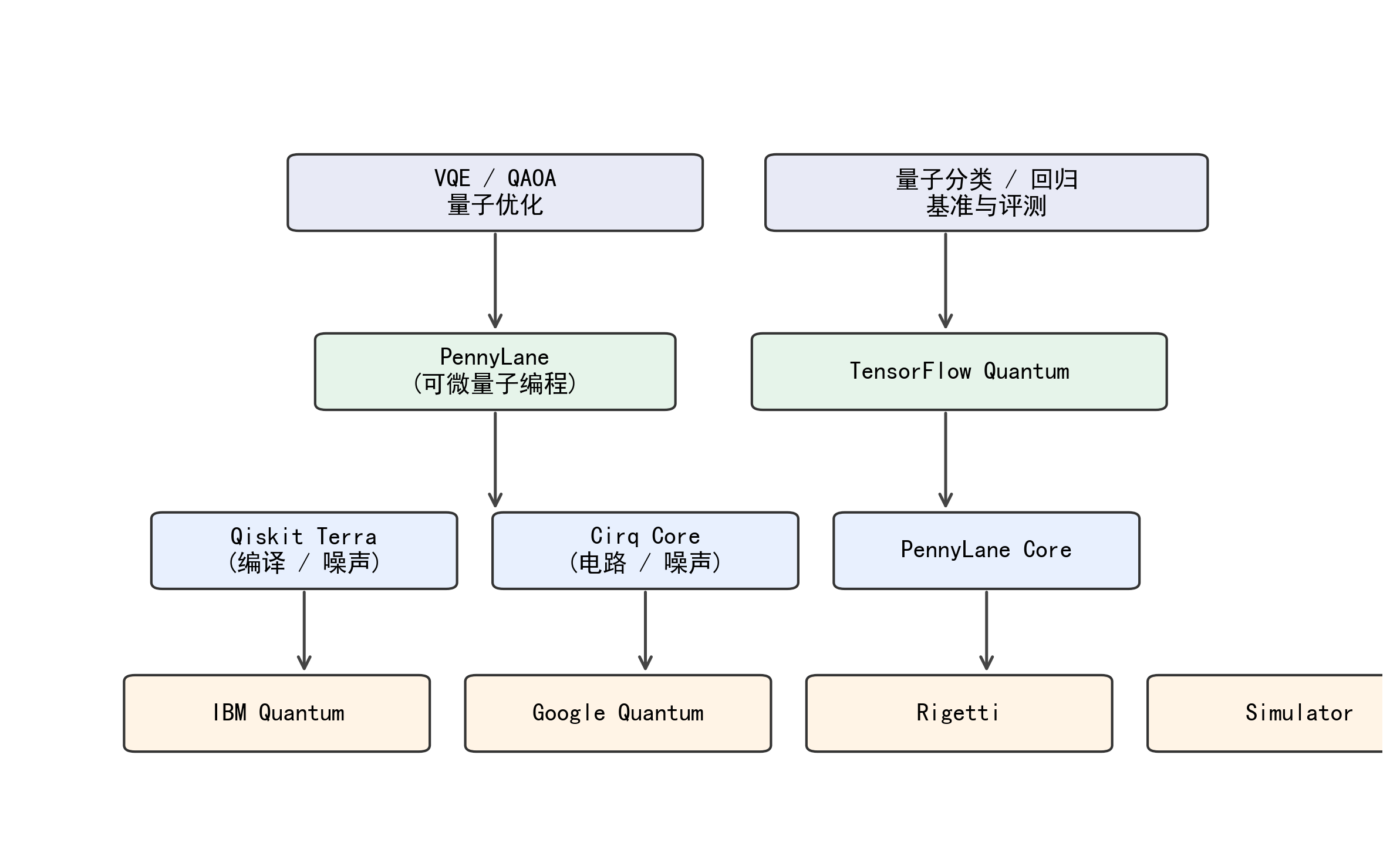
图4 量子AI软件栈分层架构图

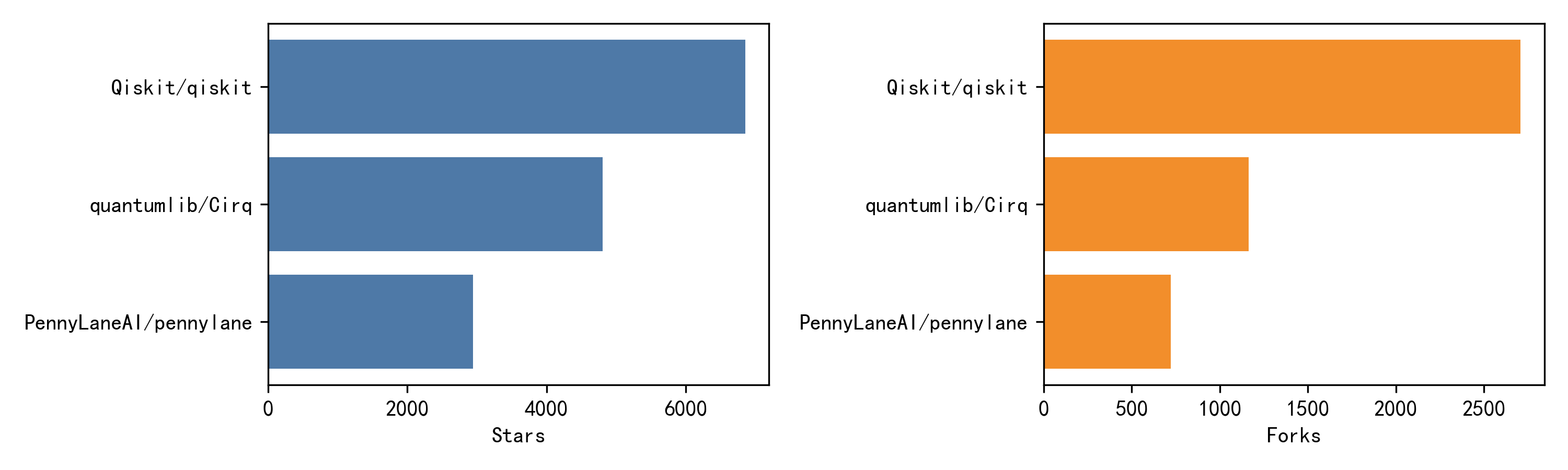
图5 GitHub 热度对比柱状图

6 Quantum-for-AI：量子资源如何改变学习计算结构

6.1 从“量子线性代数加速”到“输入模型约束”：为什么很多结论需要重新解读

在经典机器学习里，线性代数是计算瓶颈：矩阵求解、特征分解、最小二乘、核矩阵运算都可能成为大规模训练的核心成本。量子算法社区早期提出的一类思路是用量子线性代数子程序（典型如 HHL 类方法）在某些条件下实现指数或多项式加速，从而加速回归或分类。然而，量子AI语境下必须非常谨慎地解读这类结论，因为“加速”往往建立在输入以量子态形式提供、或者可以在多对数时间内加载的假设上；如果要从经典数据出发制备相应量子态，成本可能重新回到多项式甚至线性量级，从而抵消优势。经典视角的综述明确提醒：量子机器学习的复杂度比较必须把数据输入与输出读取纳入同一账本，否则“算法主体很快”并不等于“端到端很快”。

进一步说，即使在理想输入模型下，量子线性代数加速与“学习意义上的优势”也不是同一回事。学习目标关心的是泛化误差与稳定性，而不是仅仅把某个线性系统解出来。量子算法常常输出的是量子态形式的解向量，而经典学习通常需要显式参数向量或可解释的统计量，这会引入读取成本与测量误差。因此，在量子AI研究中，更常见的策略不是直接套用线性代数加速，而是把量子资源用于构造新的表示与相似度度量（例如量子核），或者用于构造具有特定统计结构的采样过程（例如量子生成模型），从而在“表示学习/核方法/采样”层面寻找优势空间。

6.2 量子核的优势条件：可模拟性、有效性与估计复杂度必须同时满足

量子核方法的理论魅力来自一个清晰的分工：量子设备用于估计核值，经典计算用于求解凸优化问题。这种结构天然便于与经典基线比较，因为核方法在经典机器学习中有成熟的泛化理论与优化理论。真正困难的是：什么样的量子核既能在计算上难以被经典有效模拟，又能在统计上对任务有区分能力。已有研究指出，单纯追求“不可模拟”可能导致核在学习意义上无效；反过来，过于简单的核虽然有效但可能经典可计算，从而失去量子加速空间。针对这一矛盾，有工作从核谱、数据分布与特征映射结构出发讨论量子核优势的必要条件，并强调要把“核估计的采样复杂度”纳入比较框架。

在工程上，量子核估计往往通过 swap test、直接重叠估计或随机测量等方式实现。无论采用哪种方式，shots 都会引入统计误差，核矩阵的噪声会影响到 SVM 的 margin 与分类边界稳定性。于是一个现实问题出现：即使量子核在理想情况下有优势，有限 shots 下的估计误差可能让训练不稳定。解决思路通常包括：对核矩阵做正则化、采用低秩近似、或通过测量分配策略集中 shots 于最关键的核元素。这类策略本质上是在“量子采样预算”约束下重新设计核学习流程，体现了量子AI与经典学习的深层耦合：量子侧给你的是带噪估计，经典侧必须用统计学习方法处理不确定性。

6.3 变分模型与“可训练量子表征”：表达能力不是越强越好

变分量子模型常被描述为“量子神经网络”，但从理论上更精确的说法是“参数化幺正族诱导的可观测期望函数族”。它的表达能力由电路结构、参数数量、纠缠模式与测量算符共同决定。表面上看，只要电路足够深，就可以逼近任意幺正，从而具备极强表达能力；但在学习语境中，表达能力必须与可训练性匹配。过强的随机电路虽然表达空间大，却更容易出现 barren plateaus，使得训练几乎不可行。系统性分析指出：可训练性与电路的局部性、目标函数的局部结构、以及初始化策略密切相关。对于量子AI而言，这意味着模型设计需要“结构化偏置”，例如采用问题启发式 ansatz（化学模拟中的 UCC、优化中的 QAOA 结构等），或者采用局部纠缠层以控制训练景观。

6.4 QAOA、VQE 与学习的关系：把目标函数写成哈密顿量是一种统一语言

在 NISQ 时代，VQE 与 QAOA 常被视为两类代表性的混合变分算法。它们与“学习”之间的关系并不只是“可以拿来做应用”，更重要的是它们提供了一个统一语言：把目标写成可观测量（尤其是哈密顿量）的期望，并用参数化电路去最小化（或最大化）这个期望。VQE 的核心思想是变分原理：任意试探态的能量期望是基态能量的上界，因此最小化能量期望可以逼近基态。形式上，若哈密顿量可分解为若干 Pauli 串之和，则能量期望可写为：

$$
E(\theta)=\langle\psi(\theta)|H|\psi(\theta)\rangle=\sum_j c_j,\langle\psi(\theta)|P_j|\psi(\theta)\rangle
$$

其中 Pj 是 Pauli 串算符，cj 是系数。这个分解直接带来一个训练成本事实：每个项的期望都需要测量估计，项数与测量分组策略会显著影响训练开销。VQE 的原始工作与后续理论分析都强调了这种“测量成本”是 NISQ 下的重要瓶颈。

QAOA 则把组合优化目标写成代价哈密顿量，并通过交替施加代价演化与混合演化构造参数化电路。其结构可以写为（用 p 层表示）：

$$
|\gamma,\beta\rangle=\prod_{k=1}^{p}e^{-i\beta_k H_M}e^{-i\gamma_k H_C},|+\rangle^{\otimes n}
$$

其中 HC 对应目标函数，HM 是混合哈密顿量。QAOA 的意义在于，它把“搜索”嵌入量子演化结构，参数学习的对象是演化时间（γ,β）。从量子AI角度看，QAOA 展示了“把优化问题写成可训练电路”的范式，许多量子学习模型本质上也是在学习某种“演化参数”，只是目标不一定是组合优化，而可能是分类损失或生成模型的对数似然。

7 AI-for-Quantum：用学习方法改造量子系统的控制、纠错与误差缓解

7.1 量子控制与校准：把脉冲设计从“人工调参”变成“与设备交互的学习”

量子硬件要实现稳定计算，离不开高精度的控制与校准。传统方法往往依赖物理建模与梯度型脉冲优化（例如 GRAPE 类方法），但在复杂噪声与漂移存在时，精确模型可能难以获得。机器学习提供了一条替代路径：不要求完整物理模型，而是通过与真实系统交互学习控制策略。一个代表性方向是强化学习控制：智能体通过试探控制动作，观察系统测量反馈，逐步学习到能实现目标门或目标态的控制序列。相关工作提出了“模型自由量子控制”的框架，强调在模型不完备或不可模拟时，通过实验反馈学习控制策略可以更现实地逼近最优控制。

从理论上看，量子控制学习的难点在于反馈信号往往稀疏（例如只在脉冲序列结束后测一次保真度），且测量有统计噪声。强化学习在这里并不是“炫技”，而是一套处理“延迟奖励 + 噪声观测”的成熟机制。更重要的是，这条路线的价值是可量化的：控制策略的改进可以直接体现在门保真度、误差率与漂移鲁棒性上，从而为后续量子AI算法提供更可靠的底座。对于量子人工智能这门交叉学科而言，AI-for-Quantum 是目前最接近“短期可验证收益”的方向之一，因为它不需要先证明某个学习任务的复杂度分离，只需要在硬件指标上做严格对照即可。

7.2 纠错与解码：当“实时解码”成为系统关键路径，AI自然进入回路

量子纠错是走向容错量子计算的核心，而解码器是纠错系统的“智能中枢”：它要把测量得到的综合征数据（syndrome）快速映射为纠错操作。传统解码往往依赖图匹配等算法，但随着码距增大与实时性要求提高，解码延迟可能成为系统瓶颈。这正是机器学习介入的天然场景：用神经网络、图网络或变体去学习综合征到纠错的映射，目标是降低延迟并保持足够低的逻辑错误率。已有研究提出用强化学习优化纠错码结构或解码策略，也有工作系统讨论神经网络解码器在近端实验中的可行性。

尤其值得注意的是，近期公开的表面码阈下运行实验把“实时解码”推到了非常具体的工程数据层面：公开论文报告在 72 量子比特处理器上实现距离5表面码并集成实时解码，在 105 量子比特处理器上实现距离7表面码。相关公开报告进一步给出实时解码吞吐与延迟量级，例如距离5的解码器平均延迟约 63 微秒，表面码周期时间约 1.1 微秒，并报告逻辑错误率抑制因子 Λ 的对照数据。这些数据对量子AI的意义非常直接：当系统进入阈下运行，解码器不再是离线工具，而是与量子硬件同步运行的实时模块，此时“学习型解码器”的价值可以用严格指标衡量，包括延迟、吞吐、以及对逻辑错误率的影响。

表5把上述公开数据整理为可引用的结构化信息，便于读者后续绘图或对照。

表5 表面码阈下运行与实时解码的公开数据（节选）

平台/公开实验描述	处理器规模（公开）	表面码距离（公开）	实时解码/周期关键数据（公开）	量子AI视角的含义
超导处理器A：集成实时解码的距离5表面码	72 量子比特	距离5	报告集成实时解码；公开报告给出平均延迟约63微秒、周期约1.1微秒（距离5）	解码成为低延迟推理任务；需要高吞吐学习/匹配算法
超导处理器B：距离7表面码量子存储	105 量子比特	距离7	报告距离7实现，并给出“超过两倍保持时间”等性质描述	更大码距下，解码复杂度与实时性压力显著上升

数据来源：72/105 量子比特、距离5/7来自公开论文摘要信息。实时解码延迟与周期来自公开报告。

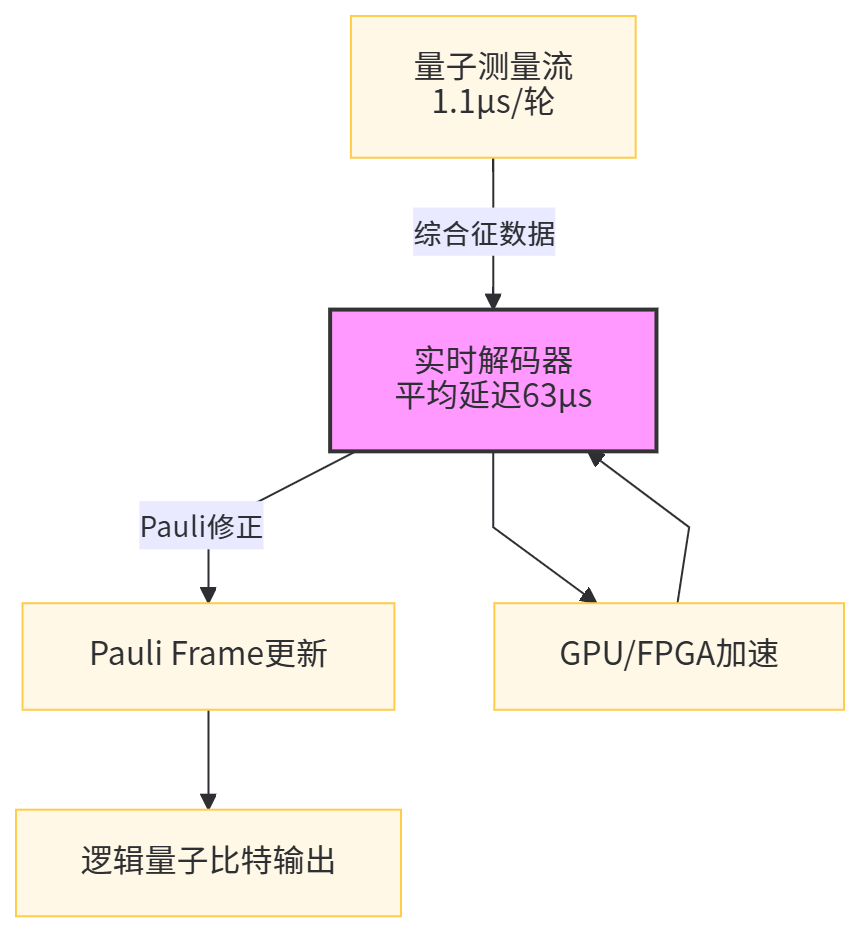
图6 表面码实时解码的数据流与时序框架图

7.3 误差缓解：从“物理纠错”到“统计修正”，机器学习可以学习噪声映射

在容错尚未普及的阶段，误差缓解（Error Mitigation）被视为 NISQ 可用性的关键补偿机制。典型方法如零噪声外推（ZNE）通过人为放大噪声并外推到零噪声极限，或用概率误差抵消等统计技术修正期望值估计。机器学习进入误差缓解的方式通常不是“替代物理”，而是学习一个从“含噪观测”到“更接近无噪目标”的映射，尤其当噪声模型复杂且时变时，学习式方法可能更具适应性。近期有工作系统性地把“机器学习用于实用误差缓解”作为研究主题，比较不同 ML 模型在多类电路与噪声轮廓下的缓解效果，并与 ZNE 等经典误差缓解策略做对照。

对量子AI而言，误差缓解的理论意义在于它把“噪声信道”显式引入学习系统：你可以把误差缓解视为一个后处理模型 g，使得目标从学习 f 变成学习 g∘f，甚至把 g 的学习纳入训练过程，形成端到端鲁棒优化。这种思路与经典机器学习中“校准/去噪/域适配”的思想相通，但量子侧更强调物理可解释性与偏差控制，因为不受控的学习式后处理可能引入难以发现的系统偏差。

8 评测与基准：如何在量子AI里讨论“可比较的进步”

8.1 指标必须区分“系统能力”与“学习能力”

量子AI评测中最容易混淆的是“硬件能力指标”和“学习任务指标”。硬件指标如量子比特数、门保真度、量子体积（Quantum Volume）或应用导向的算法级指标，反映设备能执行多复杂的电路；学习指标如分类准确率、回归误差、负对数似然、泛化 gap，则反映模型在任务上的统计性能。两类指标之间并非单调关系：更强的硬件不必然带来更好的学习性能，因为学习性能还依赖编码方式、模型结构与优化稳定性；反过来，一个学习指标的提升也可能来自更强的经典后处理而非量子部分。因此，量子AI评测需要同时报告两类指标，并明确“量子部分贡献了什么”。

8.2 算法级基准：以 AQ 为例，为什么它与量子AI有天然关系

在量子AI语境中，一个具有代表性的系统级思路是“用一组算法任务来综合评估量子计算机能否执行对应用有意义的电路”。IonQ 提出的 Algorithmic Qubits（#AQ）指标就是这种思路：它强调这是应用导向的基准，聚合多类算法的可执行规模与保真度，覆盖优化、量子模拟与量子机器学习相关的算法族。更重要的是，有公开基准论文给出了在 IonQ Forte 系统上通过 AQ 基准到 #AQ 29 的结果，并说明该系统配置为 30 量子比特的离子阱计算机。这类指标与量子AI研究的关系在于：它把“能跑多大规模的量子电路”转化为一个更贴近算法族的数值，从而比单纯的 qubit count 更接近“学习任务可行性”。

表6整理了量子AI中常用的一些“算法范式—资源特征”，目的不是给出绝对结论，而是提供一种在评测时可对照的语言：当你看到一个量子模型报告效果时，你可以问它属于哪种范式，资源瓶颈在编码、深度、shots 还是优化景观。

表6 量子AI常见算法范式与资源特征（基于公开文献的结构化归纳）

范式	典型对象	主要量子资源消耗点	训练/推断的主要统计成本	理论关注点（与量子优势相关）
量子核方法	量子特征映射 + SVM/核岭回归	特征映射电路深度；核估计电路次数	核矩阵元素估计的 shots；核噪声对泛化的影响	“不可模拟性”与“核有效性”需同时满足；核估计复杂度
变分分类/回归	PQC + 测量期望输出	参数数量与电路深度；可观测量测量分组	梯度估计需多次电路评估；shots 决定方差	barren plateaus 与可训练性；参数偏移梯度代价
VQE 类能量最小化	变分态 + 哈密顿量期望	哈密顿量项数与测量开销；ansatz 结构	每轮优化需估计多项期望值	测量成本与误差缓解；变分理论与误差抑制
QAOA 类组合优化	交替演化结构	层数 p 对电路深度线性影响	目标期望估计 + 参数搜索	结构化 ansatz 与可训练性；对照经典启发式基线
AI-for-Quantum 解码	学习型/算法型解码器	解码器本身在经典侧运行；量子侧提供综合征	实时推理延迟与吞吐；训练数据来自模拟/实验	低延迟高可靠推理；与码距扩展的复杂度关系
学习式误差缓解	ML-QEM 等	需要收集含噪观测与参考/外推数据	模型训练样本量与分布外泛化	噪声模型漂移；缓解偏差控制

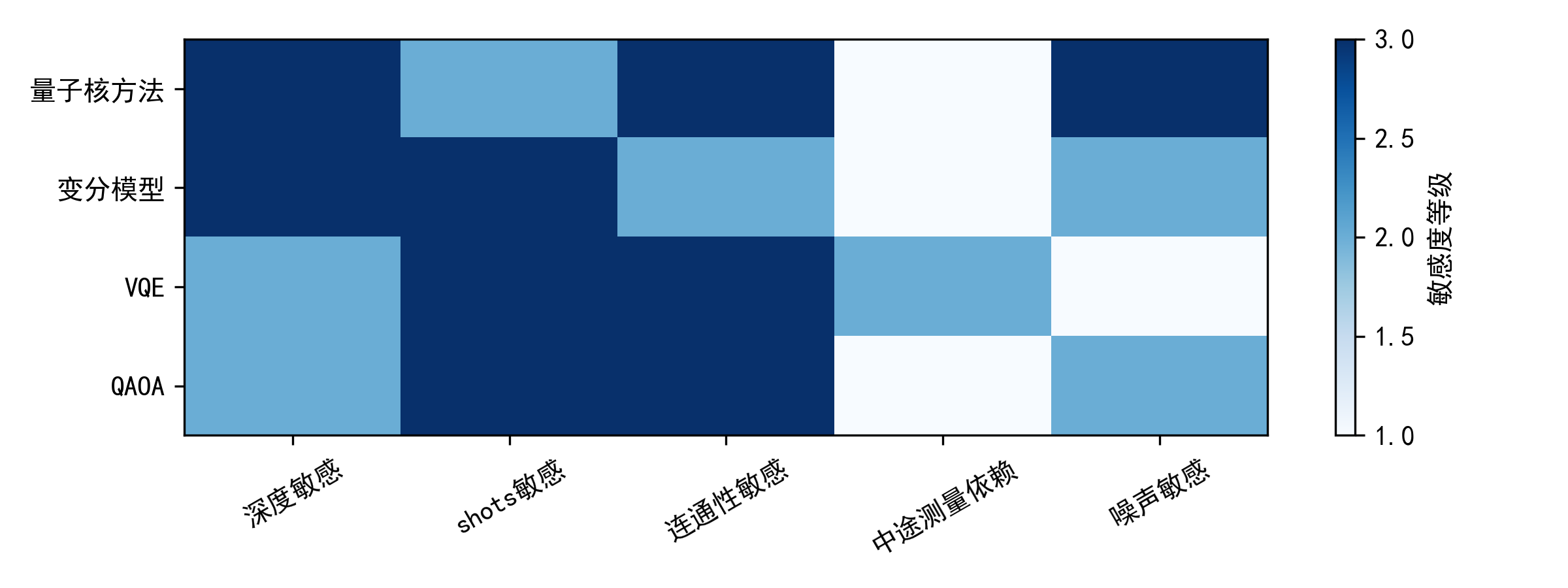
图7 算法范式—硬件约束矩阵热力图

9 关键理论难题：为什么量子AI的核心不在“想象力”，而在可证明与可验证

9.1 数据加载与输出读取：端到端复杂度账本必须闭合

量子AI最根本的理论争议之一是端到端复杂度是否真的优于经典。许多量子学习算法在主体部分可能具有对数或平方根级的复杂度优势，但这种优势往往依赖输入以量子态形式提供，或依赖某种能在多对数时间内制备量子态的假设。当我们从现实角度考虑经典数据集时，编码电路的成本必须被计入总复杂度；同样，若输出仍需以经典形式给出（例如分类标签、概率分布参数），测量读取成本也必须被计入。经典视角的量子学习综述强调，把输入/输出成本忽略掉会导致对优势的高估，因此严谨研究需要明确输入模型，并给出与最强经典基线可对照的端到端评测。

9.2 噪声与有限采样下的泛化：量子模型的统计学习理论仍在形成

在经典学习里，泛化理论讨论的是函数族复杂度、样本量与泛化误差的关系；在量子AI里，除了模型复杂度与样本量，还必须考虑“测量采样噪声”与“量子硬件噪声”。测量采样噪声类似于对损失与梯度的随机估计误差，会影响优化收敛并引入额外方差；量子硬件噪声则相当于模型本身被随机扰动，可能导致训练出的参数在不同噪声条件下迁移失败。近年来关于量子模型泛化的研究尝试把这些因素纳入分析框架，并讨论在何种结构条件下可以得到可控的泛化界。

9.3 可训练性与结构化先验：量子AI更需要“有偏置的模型设计”

barren plateaus 的讨论告诉我们：量子模型的表达能力并不能自动转化为可学得性。缓解思路往往不是“更复杂”，而是“更结构化”。结构化可以来自任务本身（例如哈密顿量局部性、对称性），也可以来自硬件拓扑（例如局部纠缠层），还可以来自训练策略（例如逐层增长、局部目标函数、问题启发式初始化）。这些策略在本质上是在假设空间中加入偏置，以换取训练信号的可获得性。值得强调的是，这种偏置并不违背“学习”的精神，恰恰相反，现代深度学习成功很大程度也来自结构偏置（卷积、注意力、归纳偏置）。量子AI只是把这种问题更加尖锐地暴露出来，因为硬件噪声与测量统计使得“靠暴力训练”更不可行。

10 结语：把量子人工智能当作“可推导、可验证、可复现”的科学对象

量子人工智能的核心价值，不在于把“量子”与“AI”两个热词拼接，而在于它迫使我们用更严格的方式回答学习问题：当计算资源从经典比特扩展到量子态，学习的表示空间、计算结构与误差来源都发生变化，我们能否在某些明确的输入模型、硬件约束与评测协议下，证明或观察到学习意义上的优势；同时，当量子硬件走向更大规模与更复杂控制，传统工程方法是否会在实时性与复杂度上遇到瓶颈，从而让机器学习成为系统关键路径的一部分。前者要求我们在核方法、变分模型、采样机制与学习理论之间建立闭合的复杂度账本；后者要求我们把控制、校准、纠错、误差缓解这些“硬问题”形式化为可学习的目标，并以严格指标验证收益。NISQ 时代的综述与实验数据共同表明：量子AI不会以“单点奇迹”的方式突然改变一切，它更可能以一系列可度量的、逐步积累的系统改进与理论澄清向前推进。把视野放在理论骨架与真实数据上，才能让这门交叉学科走得更稳、更远。

参考资料（精选，主要为期刊/会议/预印本与官方技术资料）

[1] John Preskill. Quantum Computing in the NISQ era and beyond. Quantum 2, 79 (2018).
[2] Jacob Biamonte, Peter Wittek, Nicola Pancotti, Patrick Rebentrost, Nathan Wiebe, Seth Lloyd. Quantum machine learning. Nature 549, 195–202 (2017).
[3] Carlo Ciliberto et al. Quantum machine learning: a classical perspective. Proc. R. Soc. A 474:20170551 (2018).
[4] Kishor Bharti et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 94, 015004 (2022).
[5] Vojtěch Havlíček et al. Supervised learning with quantum-enhanced feature spaces. Nature (2019).
[6] Jarrod R. McClean et al. The theory of variational hybrid quantum-classical algorithms. arXiv:1509.04279.
[7] Alberto Peruzzo et al. A variational eigenvalue solver on a quantum processor. arXiv:1304.3061.
[8] Edward Farhi, Jeffrey Goldstone, Sam Gutmann. A Quantum Approximate Optimization Algorithm. arXiv:1411.4028.
[9] Maria Cerezo et al. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nat. Commun. (2021).
[10] Jwo-Sy Chen et al. Benchmarking a trapped-ion quantum computer with 30 qubits. arXiv:2308.05071 (IonQ Forte, #AQ 29).
[11] Quantinuum 官方博客：System Model H2 从 32 升级到 56 物理量子比特（全连接描述）。
[12] D-Wave 官方资料：Advantage 系统 5000+ qubits、15-way 连接性、35000+ couplers（数据表与介绍）。
[13] Rigetti 官方/合作方公开信息：Ankaa-2 84-qubit 系统与两比特门保真度披露。
[14] 公开论文：表面码阈下运行（72-qubit 距离5；105-qubit 距离7）。
[15] APS 公开报告：实时解码延迟与周期等工程数据（距离5延迟约63微秒、周期约1.1微秒等）。
[16] PhysRevX：Model-Free Quantum Control with Reinforcement Learning（量子控制的学习范式）。
[17] arXiv:2309.17368 Machine Learning for Practical Quantum Error Mitigation（学习式误差缓解基准与方法）。
[18] IBM Quantum Roadmap（处理器节点与规模公开资料）。
[19] Google quantumlib/Cirq、Qiskit、PennyLane、TensorFlow Quantum 的 GitHub 页面（stars/forks 公开数据）。