【论文精读】Mosquito detection with neural networks: the buzz of deep learning

-1

最新推荐文章于 2025-11-24 11:49:49 发布

原创最新推荐文章于 2025-11-24 11:49:49 发布 · 1.2k 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #人工智能

人工智能新时代同时被 2 个专栏收录

47 篇文章

订阅专栏

深度学习论文精读与代码复现

23 篇文章

订阅专栏

本文精读的论文为《Mosquito Detection with Neural Networks: The Buzz of Deep Learning》，作者是来自牛津大学工程系和动物系的Ivan Kiskin等研究团队。该论文发表于2017年，是一篇关于使用深度学习技术检测蚊子声音信号的重要研究。

蚊子作为疟疾、寨卡病毒、登革热等疾病的传播媒介，每年导致数十万人死亡。准确快速地检测和识别蚊子对于疾病预防和控制具有重要意义。传统的蚊子检测方法主要依赖人工捕获或光阱，效果有限且成本高昂。该论文提出了一种基于声学信号的自动检测方法，利用蚊子飞行时产生的声音特征进行识别。

1. 摘要

许多现实世界的时间序列分析问题都以数据稀缺为特征。解决方案通常依赖于从时域或频域提取的手工制作特征，结合分类或回归引擎，这些引擎以此类（通常是低维的）特征向量为条件。近年来许多应用领域取得的巨大进步都是由在大型数据集上训练的深度学习架构的使用所推动的。本文提出了一种深度学习方法用于声学事件检测，应用于一个具有挑战性的、数据稀缺的现实问题。我们的候选挑战是从蚊子的声学特征中准确检测蚊子的存在。我们开发了在音频记录的小波变换上操作的卷积神经网络（CNNs）。此外，我们通过可视化网络激励样本的统计信息来审查网络的预测能力。这些可视化为检测问题中各组件的相对信息性提供了深入的洞察。我们包含了与传统分类器的比较，这些分类器以手工调整和通用特征为条件，以强调自动深度特征学习的优势。检测是通过显著超越现有算法方法的性能指标来实现的，甚至略微超过了个别人类专家所达到的水平。与本文相关的数据和软件可在 http://humbug.ac.uk/kiskin2017/ 获得。

关键词： 卷积神经网络，频谱图，短时傅里叶变换，小波，声学信号处理

2. 引言

蚊子由于其传播致命寄生虫和病毒的能力，每年造成数十万人死亡，这些疾病包括疟疾、淋巴丝虫病、寨卡病毒、登革热和黄热病[35,34]。它们传播疾病的能力已被广泛了解超过一百年，并已实施若干做法来减轻其对人类生活的影响。

这些做法的例子包括杀虫剂处理的蚊帐[19,4]和不育昆虫技术[3]。然而，在对抗蚊媒疾病的斗争中取得进一步进展需要更准确地识别物种及其精确位置——并非所有蚊子都是疾病载体，一些非载体在形态学上与高效载体物种相同。目前的调查要么依赖人体着陆捕获，要么依赖效果较差的光阱。这部分是由于缺乏便宜而准确的监视传感器来协助蚊子检测。我们的工作使用蚊子飞行的声学特征作为检测的触发器。蚊子的声学监测具有吸引力，因为昆虫既作为其飞行的副产品产生声音，又作为通信和交配的手段。检测和识别这种声音是定位蚊子存在的有效方法，甚至提供了按物种分类的可能性。尽管如此，自动蚊子检测呈现了一个基本的信号处理挑战，即检测嵌入在噪声中的弱信号。当前的检测机制严重依赖领域知识，如可能的基频和谐波，以及特征的广泛手工制作——通常类似于传统的语音表示。随着深度学习在许多应用领域（包括生物声学[16]）取得令人印象深刻的性能提升，出现了利用这些进展来解决这个问题的机会。

然而，深度学习方法往往只有在达到训练样本的临界数量后才有效[6]。因此，数据稀缺问题不太适合这种范式。与许多其他领域一样，数据标记任务在时间要求方面和相关模糊性方面都很昂贵——即多个人类专家在其标签上不会完全一致。此外，现实环境中自由飞行蚊子的记录是稀缺的[23]，几乎从未被标记。

本文提出了一种使用稀缺训练数据分类蚊子存在的新方法。我们的方法基于以原始数据的小波表示为条件的卷积神经网络分类器。网络架构和相关超参数受到数据集大小约束的强烈影响。为了评估我们的性能，我们将我们的方法与建立良好的分类器以及简单的人工神经网络进行比较，这些神经网络在手工制作特征和短时傅里叶变换上训练。我们表明我们的分类更加准确和自信，产生0.909的精确率-召回率曲线面积，相比之下最高得分的传统分类器和密集层神经网络分别为0.831和0.875。这种性能是在分类任务上实现的，其中只有70%的标签在四个领域专家之间完全一致。我们取得了与人类专家水平准确率匹配甚至超越的结果。我们方法的性能允许作为智能手机应用程序或定制嵌入式系统进行现实的现场部署。

本文的结构如下。第2节讨论相关工作，解释我们方法的动机和好处。第3节详细介绍我们采用的方法。第4节描述实验设置，特别强调数据驱动的架构设计决策。第5节突出该方法的价值。我们在第5.1节中可视化和解释我们算法对未见数据的预测，以帮助揭示从表示中学到的信息特征并验证方法。最后，我们在第6节中建议进一步的工作并得出结论。

3. 相关工作

人工神经网络在物种声学检测和分类中的使用至少可以追溯到本世纪初，第一批方法涉及蝙蝠回声定位叫声的识别[25]。随后，手动和算法技术都被用于识别昆虫[7,36]、大象[8]、海豚[24]和其他动物。利用动物产生的声音的好处——既作为通信机制主动产生，又作为运动结果被动产生——是明显的：动物本身使用声音来识别猎物、捕食者和配偶。因此，声音可以用于定位个体进行生物多样性监测、害虫控制、濒危物种识别等。

因此，本节将回顾机器学习方法在生物声学中的使用，特别是关于昆虫识别。我们描述传统的特征和分类方法用于声学信号检测。相反，我们也呈现当前深度学习方法固有的特征提取方法的好处。最后，我们将焦点缩小到经常被忽视的小波变换，它在我们的管道中提供了显著的性能提升。

3.1 昆虫检测

实时蚊子检测提供了对抗致命疾病传播的方法，主要是疟疾、黄热病和登革热。与直翅目（蟋蟀和蚱蜢）和半翅目（例如蝉）不同，它们产生强烈的定位和交配叫声，蚊子（双翅目，库蚊科）要安静得多。它们发出的噪音是由翅膀拍打产生的，受到一系列不同变量的影响，主要是物种、性别、年龄、温度和湿度。在野外，翅膀拍打声音经常被环境噪音淹没。由于这些原因，蚊子的实验室记录通常在安静或甚至隔音的房间中对束缚的蚊子进行，因此不代表现实条件。

即使在这种数据稀缺的情况下，人工神经网络的使用已经被证明在许多年中是成功的。在[7]中，使用神经网络分类器来区分在英格兰北部记录的四种蚱蜢，准确率超过70%。其他分类方法包括高斯混合模型[29,26]和隐马尔可夫模型[20,36]，应用于从歌唱昆虫记录中提取的各种不同特征。

Chen等人[6]将自动昆虫检测准确率的停滞归因于仅使用声学设备，据称这些设备无法产生足够清洁的信号以正确分类。因此，他们用伪声学光学传感器替换麦克风，通过激光束撞击光电晶体管阵列记录蚊子翅膀拍打——这种做法已经由Moore等人[22]提出。然而，这种技术依赖于能够引诱蚊子穿过激光束的能力。

无论使用何种技术记录蚊子翅膀拍打频率，都需要能够在嘈杂记录中识别昆虫飞行。以下部分回顾了在更广泛的声学信号分类背景下的最近成就。

3.2 特征表示和学习

自动检测噪音中声学信号的过程通常包括初始预处理阶段，涉及信号本身的清洁和去噪，然后是特征提取过程，其中信号被转换为适合分类器的格式，然后是最终分类阶段。历史上，音频特征提取在信号处理中使用了领域知识和对数字信号理论的复杂理解[15]，导致手工制作的特征表示。

许多这些表示经常在文献中出现。一种强大但经常被忽视的技术是小波变换，它具有表示多个时频分辨率的能力[2, Ch. 9]。其中具有固定时频分辨率的实例化是傅里叶变换。傅里叶变换可以用平滑窗函数进行时间窗化以创建短时傅里叶变换（STFT）。梅尔频率倒谱系数（MFCCs）通过获取STFT、应用非线性变换（对数）、池化和最终仿射变换来创建低维表示。另一个例子由线性预测倒谱系数（LPCCs）呈现，它预先强调低频分辨率，然后进行线性预测和倒谱分析[1]。

检测方法已将通用STFT表示馈送到标准分类器[27]，但更经常使用复杂特征和特征组合，应用降维来对抗维度诅咒[18]。复杂特征（例如MFCCs和LPCCs）最初是为特定应用（如语音识别）开发的，但此后已在几个音频领域中使用[21]。

相反，深度学习方法通常包括对输入数据应用简单的通用变换，并允许网络既学习特征又执行分类。这使得模型能够从原始数据中学习显著的、层次化的特征。自动深度学习方法最近在机器学习文献中占据突出地位，在各种应用领域显示出令人印象深刻的结果，如计算机视觉[17]和语音识别[18]。然而，深度学习模型（如卷积和递归神经网络）已知具有大量参数，因此通常需要大型数据和硬件资源。尽管成功，这些技术直到最近才在时间序列信号处理中得到更多关注。

这种方法论转变的一个突出例子是BirdCLEF鸟类识别挑战。该挑战包括将鸟类歌曲和叫声分类为来自数万个众包记录的多达1500种鸟类。深度学习的引入带来了平均平均精度（MAP）分数的巨大改进。2014年的最佳MAP分数是0.45[11]，次年当引入深度学习时提高到0.69，超过了得分0.58的最接近的手工制作方法[16]。令人印象深刻的性能提升来自利用图像识别中建立良好的卷积神经网络实践。通过将信号转换为STFT频谱图格式，输入由2D矩阵表示，用作训练数据。除了这个例子，转换输入信号最广泛使用的基本方法是STFT[30,14,28]。

然而，据我们所知，更灵活的小波变换很少用作卷积神经网络的表示域。因此，在下一节中，我们呈现我们的方法论，它利用了在信号处理文献中展示的小波变换的好处，以及为深度学习形成层次特征表示的能力。

4. 基础知识详解

在深入理解本文的核心方法之前，我们需要详细了解几个关键的技术基础。这些概念不仅是理解论文方法的前提，也是音频信号处理和深度学习领域的重要组成部分。

4.1 音频信号的数字表示与时频分析

音频信号在自然界中以连续的模拟波形存在，包含了丰富的时间和频率信息。当我们需要在数字系统中处理这些信号时，必须通过采样和量化过程将其转换为离散的数字表示。采样频率决定了我们能够捕捉到的最高频率成分，根据奈奎斯特定理，采样频率必须至少是信号最高频率成分的两倍才能完全重构原信号而不产生混叠。在蚊子检测的应用场景中，蚊子翅膀拍打产生的声音通常包含从几百赫兹到数千赫兹的频率成分，因此需要选择合适的采样频率来确保重要信息不会丢失。

传统的傅里叶变换能够将时域信号完全转换为频域表示，揭示信号中包含的所有频率成分及其强度。然而，傅里叶变换的一个根本限制是它丢失了时间信息——我们可以知道信号中存在某个频率成分，但无法确定这个频率成分在什么时候出现。对于像蚊子飞行这样的非平稳信号，频率成分随时间的变化携带了关键的识别信息，因此需要能够同时保留时间和频率信息的分析方法。

4.2 短时傅里叶变换的原理与局限性

短时傅里叶变换（STFT）通过引入滑动窗口的概念解决了传统傅里叶变换缺乏时间定位能力的问题。STFT的基本思想是使用一个固定大小的窗函数在信号上滑动，对每个窗口内的信号片段进行傅里叶变换，从而获得信号在不同时间段的频率特征。数学上，STFT可以表示为：

$STFT(m,\omega) = \sum_{n=-\infty}^{\infty} x[n]w[n-m]e^{-j\omega n}$

其中 $x[n]$ 是输入信号， $w[n]$ 是窗函数， $m$ 表示时间位置， $\omega$ 表示频率。通过这种方式，我们可以构建一个二维的时频图，横轴表示时间，纵轴表示频率，图像的亮度或颜色表示对应时间和频率位置的能量强度。

然而，STFT存在一个固有的时频分辨率权衡问题，这是由海森堡不确定性原理所决定的。当我们选择较短的窗函数时，能够获得良好的时间分辨率，但频率分辨率会变差；相反，当选择较长的窗函数时，频率分辨率提高，但时间分辨率下降。这种权衡意味着我们无法同时在时间和频率上都达到任意高的分辨率。对于蚊子检测这样的应用，蚊子翅膀拍打既包含需要精确频率定位的基频成分，也包含需要精确时间定位的瞬态特征，因此STFT的固定分辨率限制了其表现能力。

4.3 小波变换的多分辨率优势

小波变换为时频分析提供了一种更加灵活和自适应的解决方案。与STFT使用固定窗口不同，小波变换使用可缩放和平移的小波函数作为基函数。连续小波变换的数学表达式为：

$W(a,b) = \frac{1}{\sqrt{a}} \int_{-\infty}^{\infty} x(t) \psi^*\left(\frac{t-b}{a}\right) dt$

其中 a 是尺度参数，控制小波的伸缩；b 是平移参数，控制小波在时间轴上的位置； $\psi(t)$ 是母小波函数。这种设计使得小波变换具有多分辨率分析的能力：对于高频成分，使用小尺度的小波函数，提供高时间分辨率但相对较低的频率分辨率；对于低频成分，使用大尺度的小波函数，提供高频率分辨率但相对较低的时间分辨率。

这种自适应的时频分辨率特性使小波变换特别适合分析像蚊子声音这样的非平稳信号。蚊子翅膀拍打产生的基频通常相对稳定，需要精确的频率分析来识别不同种类的蚊子；同时，翅膀拍打的开始、结束以及强度变化等瞬态特征需要精确的时间定位。小波变换能够在同一分析中同时满足这两种不同的分辨率需求。

4.4 Bump小波的特殊性质

在本研究中，作者选择了bump小波作为分析的基础。Bump小波在频域中的表达式为：

$\Psi(s\omega) = \exp\left(1 - \frac{1}{1 - (s\omega - \mu)^2/\sigma^2}\right) I_{[(\mu - \sigma)/s,(\mu + \sigma)/s]}$

这里 $I[\cdot]$ 是示性函数，s 是小波尺度， $\mu$ 和 $\sigma$ 是控制小波形状的参数。Bump小波的一个重要特性是它在频域中具有紧支撑性，即它只在有限的频率范围内非零。参数 $\mu$ 控制小波的中心频率，较大的 $\mu$ 值对应较高的中心频率；参数 $\sigma$ 控制频率带宽，较小的 $\sigma$ 值会产生更窄的频带，从而提供更好的频率选择性，但同时会降低时间定位精度。

这种可调节的频率选择性使得bump小波非常适合蚊子声音分析。通过适当选择 $\mu$ 和 $\sigma$ 参数，可以设计出对蚊子翅膀拍打频率范围（通常在150-1000Hz之间）具有最佳响应的小波函数。同时，bump小波的光滑性质有助于减少分析过程中的边界效应和数值不稳定性。

4.5 卷积神经网络的深层架构原理

卷积神经网络（CNN）是深度学习中专门用于处理具有网格状拓扑结构数据的神经网络架构，如时间序列数据（一维网格）或图像数据（二维网格）。CNN的核心思想是通过卷积操作提取输入数据的局部特征，然后通过多层网络学习从低级特征到高级语义特征的层次化表示。

卷积操作的数学定义为：

$Y_k(i,j) = X * W_p = \sum_{i'} \sum_{j'} X(i-i', j-j') W_p(i', j')$

其中 X 是输入特征图， $W_p$ 是第 p 个卷积核， $Y_k$ 是输出特征图。卷积操作具有几个重要的数学性质：首先是参数共享，同一个卷积核在输入的不同位置进行相同的计算，大大减少了需要学习的参数数量；其次是平移等变性，如果输入发生平移，输出也会发生相应的平移，这对于检测任务特别有用，因为我们希望网络能够在输入信号的任何位置识别目标模式。

在处理小波变换得到的时频图时，CNN的这些特性发挥了重要作用。小波时频图中的蚊子特征可能出现在时间轴的任何位置，平移等变性确保了网络能够一致地识别这些特征。同时，蚊子声音的局部结构（如谐波模式、基频及其倍频等）可以通过卷积操作有效提取，而参数共享机制确保了这些模式检测器可以在整个时频图上重复使用。

4.6 激活函数与网络非线性

神经网络的表达能力很大程度上依赖于激活函数引入的非线性。在本研究中，作者选择了修正线性单元（ReLU）作为主要的激活函数。ReLU函数定义为 $f(x) = \max(0, x)$ ，虽然形式简单，但具有几个重要优势。

首先，ReLU函数计算高效，只需要一个阈值比较和选择操作，相比sigmoid或tanh等传统激活函数，不涉及指数计算，大大提高了训练和推理的速度。其次，ReLU函数能够缓解梯度消失问题，这是深度网络训练中的一个重要挑战。在传统的sigmoid函数中，当输入值较大或较小时，梯度接近零，导致深层网络的梯度难以有效传播；而ReLU函数在正值区域的梯度恒为1，有助于梯度的稳定传播。

更重要的是，ReLU函数的稀疏激活特性对于音频信号处理特别有意义。在蚊子检测的场景中，大部分时间和频率区域可能不包含有用的信息，只有特定的时频模式才对分类有价值。ReLU的稀疏性使得网络能够自动关注这些重要的激活区域，抑制背景噪声和无关信息的影响。

4.7 正则化技术与过拟合防止

在数据稀缺的情况下，过拟合是深度学习面临的主要挑战。本研究采用了dropout正则化技术来缓解这个问题。Dropout的基本思想是在训练过程中随机将某些神经元的输出设置为零，从而强制网络不依赖特定的神经元组合来做出决策。

数学上，dropout可以表示为：在训练时，对于每个神经元，以概率 p 将其输出设置为0，以概率 1-p 保持原值并按比例缩放；在测试时，所有神经元都参与计算，但输出需要按 1-p 的比例进行缩放以保持期望值的一致性。这种随机性迫使网络学习更加鲁棒的特征表示，因为它不能过分依赖任何单个特征或神经元。

在蚊子检测的背景下，dropout帮助网络学习到更加泛化的声学特征，而不是过度拟合训练数据中的特定噪声模式或录制条件。这对于实际应用特别重要，因为实际环境中的蚊子声音可能与实验室条件下的训练数据存在差异。

4.8 多层感知器与卷积网络的对比

为了验证卷积结构的有效性，本研究还实现了多层感知器（MLP）作为对比基线。MLP是最基础的神经网络结构，由全连接层组成，每个神经元与前一层的所有神经元相连。在处理时频图数据时，MLP需要将二维的时频图展平为一维向量作为输入。

MLP与CNN的根本差异在于连接模式和归纳偏置。MLP的全连接结构意味着每个输出都依赖于输入的每个元素，这种全局连接虽然提供了最大的灵活性，但也意味着网络需要从头开始学习时频图中的空间结构关系。相比之下，CNN通过局部连接和参数共享显式地编码了输入数据的空间结构假设。

对于时频图这样具有明显空间结构的数据，CNN的归纳偏置是合理的：相邻的时间点和频率点之间通常存在强相关性，而距离较远的点之间的直接关系相对较弱。蚊子的声学特征通常表现为时频图中的连续区域或特定的几何模式（如谐波结构表现为平行的水平条纹），这些模式正是卷积操作擅长捕捉的。

4.9 损失函数与优化策略

在二分类任务中（检测蚊子存在与否），交叉熵损失函数是标准选择。对于样本 $(x_i, y_i)$ ，其中 $y_i \in {0, 1}$ 是真实标签， $\hat{y}_i$ 是网络预测的概率，交叉熵损失定义为：

$L = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)]$

交叉熵损失函数不仅惩罚错误分类，还鼓励网络对正确分类产生高置信度的预测。这种特性对于蚊子检测任务特别有价值，因为我们不仅希望网络能够正确分类，还希望它能够提供可靠的置信度估计，这对于实际应用中的决策制定很重要。

优化过程通常采用随机梯度下降（SGD）或其变种，如Adam优化器。这些优化算法通过反向传播算法计算损失函数关于网络参数的梯度，然后更新参数以最小化损失。在数据稀缺的情况下，优化策略的选择尤为重要，需要在快速收敛和避免过拟合之间找到平衡。

5. 方法

我们提出了一种新颖的基于小波变换的卷积神经网络架构，用于检测嘈杂音频记录中蚊子的飞行音调。我们在算法的背景下解释小波变换，然后描述神经网络配置和一系列传统分类器，我们用来评估性能。特征提取和分类管道的关键步骤在算法1中给出。

算法1 检测管道

加载N个标记的麦克风记录 $x_1(t), x_2(t), \ldots, x_N(t)$ 。
使用 $h_1$ 特征进行变换，使我们形成特征张量 $X_{train}$ 和相应的标签向量 $y_{train}$ ：

$X_{train} \in \mathbb{R}^{N_S \times h_1 \times w_1}, \quad y_{train} \in \mathbb{R}^{N_S \times 2}$

其中 $N_s$ 是通过将变换的记录分割成维度为 $h_1 \times w_1$ 的2D"图像"形成的训练样本数。
在 $X_{train}, y_{train}$ 上训练分类器。
对于测试数据 $X_{test}$ ，神经网络为每个类别 $C_i$ 输出预测 $y_{i,pred}$ ： ${C_0 = nonmosquito, C_1 = mosquito}$ ，其中

$0 \leq y_{i,pred}(x) \leq 1, \quad \text{let} \sum_{i=1}^{n} y_{i,pred}(x) = 1$

5.1 小波变换

作为初始步骤，我们将训练数据提取为适合分类器的格式。我们选择使用连续小波变换（CWT），因为它在时频分析中的成功应用[9]（算法1的步骤2）。给定小波尺度和中心频率之间的直接关系，我们使用bump小波[33]，在傅里叶域中表达为：

$\Psi(s\omega) = \exp\left(1 - \frac{1}{1 - (s\omega - \mu)^2/\sigma^2}\right) I_{[(\mu - \sigma)/s,(\mu + \sigma)/s]}$

其中 $I[\cdot]$ 是指示函数， $s$ 是小波尺度。高 $\mu$ 值以及小 $\sigma$ 值导致具有优越频率定位但较差时间定位的小波。

[图片位置：小波变换示意图]

5.2 神经网络配置

卷积层 $H_{conv} : \mathbb{R}^{h_1 \times w_1 \times c} \rightarrow \mathbb{R}^{h_2 \times w_2 \times N_k}$ ，具有输入张量 $X \in \mathbb{R}^{h_1 \times w_1 \times c}$ 和输出张量 $Y \in \mathbb{R}^{h_2 \times w_2 \times N_k}$ ，通过将 $N_k$ 个可学习卷积核 $W_p \in \mathbb{R}^{k \times k},p < N_k$ 顺序应用到输入张量来给出。给定我们的单通道（c = 1）信号输入表示 $X \in \mathbb{R}^{h_1 \times w_1 \times 1}$ 和单个核 $W_p$ ，它们的2D卷积 $Y_k$ 由[12, Ch. 9]给出：

$Y_k(i,j) = X * W_p = \sum_{i'} \sum_{j'} X(i-i', j-j') W_p(i', j')$

$N_k$ 个单独输出然后通过非线性函数 $\phi$ 传递并作为张量 Y 堆叠。激活 $\phi$ 的常见选择包括sigmoid函数、双曲正切和修正线性单元（ReLU）。

全连接层 $H_{FC} : \mathbb{R}^m \rightarrow \mathbb{R}^n$ ，具有输入 $x \in \mathbb{R}^m$ 和输出 $y \in \mathbb{R}^n$ ，由 $y = H_{FC}(x) = \phi(Wx + b)$ 给出，其中 ${W, b}$ 是网络的可学习参数， $\phi$ 是层的激活函数，通常选择为非线性。

数据大小约束导致架构选择（图1）的层数少和自由参数少。为了防止过拟合，我们的网络包含一个输入层，顺序连接到单个卷积层和全连接层，后者连接到两个输出类别，带有dropout[32]， $p = 0.5$ 。基于其理想的训练收敛特性[17]，采用修正线性单元（ReLU）激活。最后，潜在候选超参数通过交叉验证确定适当模型，详见第4.2节。

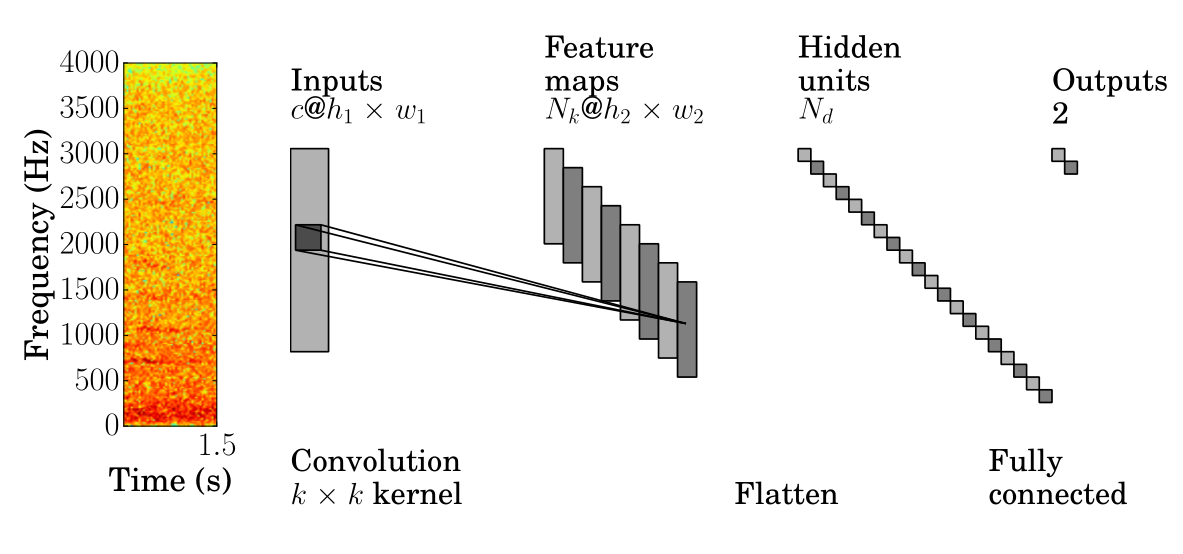
[图1：CNN管道。1.5秒蚊子记录的小波频谱图被分割成具有c=1通道、尺寸为h1×w1的图像。这作为输入到具有Nk个滤波器的卷积网络，核Wp ∈ R^k×k。特征图在卷积后形成，尺寸减少到h2×w2。这些图被完全连接到密集层中的Nd个单元，完全连接到输出层中的2个单元。]

使用传统多层感知器（MLP），可以简单地将矩阵 X 折叠成单列向量 x。与其卷积对应物不同，MLP没有明确要求在相邻神经元之间寻找关系。虽然这可能为模型提供更多灵活性来找到看似遥远节点之间的关系，但卷积层形式上使模型承认单元在空间上相关。没有这种假设，MLP将在没有明确约束的空间中寻找权重集。我们的MLP架构，选择与CNN进行比较，在图2中说明。网络省略了卷积层，采用输入层形式，然后是两个全连接层，对输出节点的连接有dropout，p = 0.5。

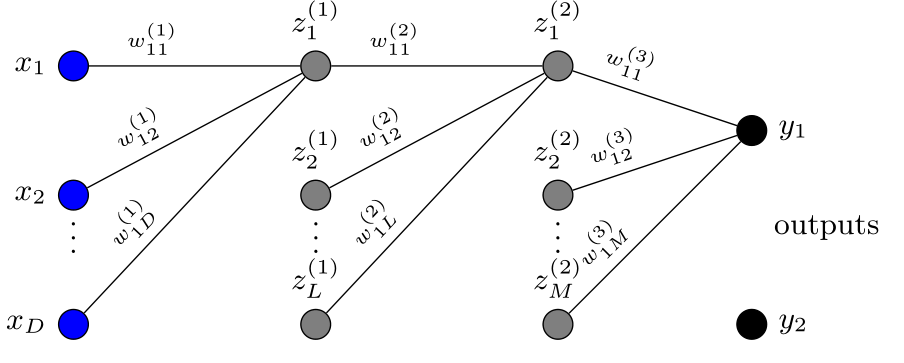
[图2：MLP架构。为了清晰，图表显示了少数单元的连接。每层完全连接，具有ReLU激活。输入维度D = h1 × w1。第一层和第二层中的隐藏单元数分别标记为L和M。]

5.3 传统分类器基线

作为基线，我们将神经网络模型与需要显式特征设计的更传统分类器进行比较。我们选择三个在音频机器学习中广泛使用的候选分类器：随机森林（RF）、朴素贝叶斯（NB）和使用径向基函数核的支持向量机（RBF-SVM）。它们的流行源于易于实现、相当快的训练和竞争性能[31]，特别是在数据稀缺问题中。

我们选择了十个特征：梅尔频率倒谱切片、STFT频谱图切片、梅尔频率倒谱系数、熵、能量熵、频谱熵、通量、滚降、扩散、质心和零交叉率（有关这些特征的详细解释，见例如[10]的开源音频信号分析工具包）。为了最优地选择特征，我们应用了递归特征消除（RFE）和主成分分析（PCA），并且还单独交叉验证了每个特征。通过减少冗余描述符，我们可以在速度和预测能力方面提高分类性能，这由第4.2节的交叉验证结果确认。

6. 实验细节

6.1 数据标注

这里使用的数据于2016年1月在包含雄性和雌性致倦库蚊的培养笼内记录[5]。雌性未喂血，两性都维持在10% w/v蔗糖溶液的饮食上。图3显示了在窗口频域中特别微弱记录的频域摘录。为了比较，我们还展示了使用与STFT中频率箱相同数量尺度 $h_1$ 的小波标量图。我们绘制每个特征表示的导出系数的绝对值的对数与光谱频率。

信号以 $F_s = 8$ kHz采样，这将最高理论可解析频率限制为4 kHz，由于奈奎斯特极限。图3（下）显示 $y_i = {0, 1}$ 内的分类：缺席，四个个别人类专家标记的蚊子存在。其中，一个特别准确的标签集被作为金标准参考来训练算法和与其余专家进行基准测试。结果标签率给定为 $F_l = 10$ Hz。标签被上采样以匹配光谱特征频率 $F_{spec}$ ，计算为 $F_{spec} = F_s/h_1$ ，条件是窗口傅里叶变换之间的样本重叠是傅里叶系数数量的一半。

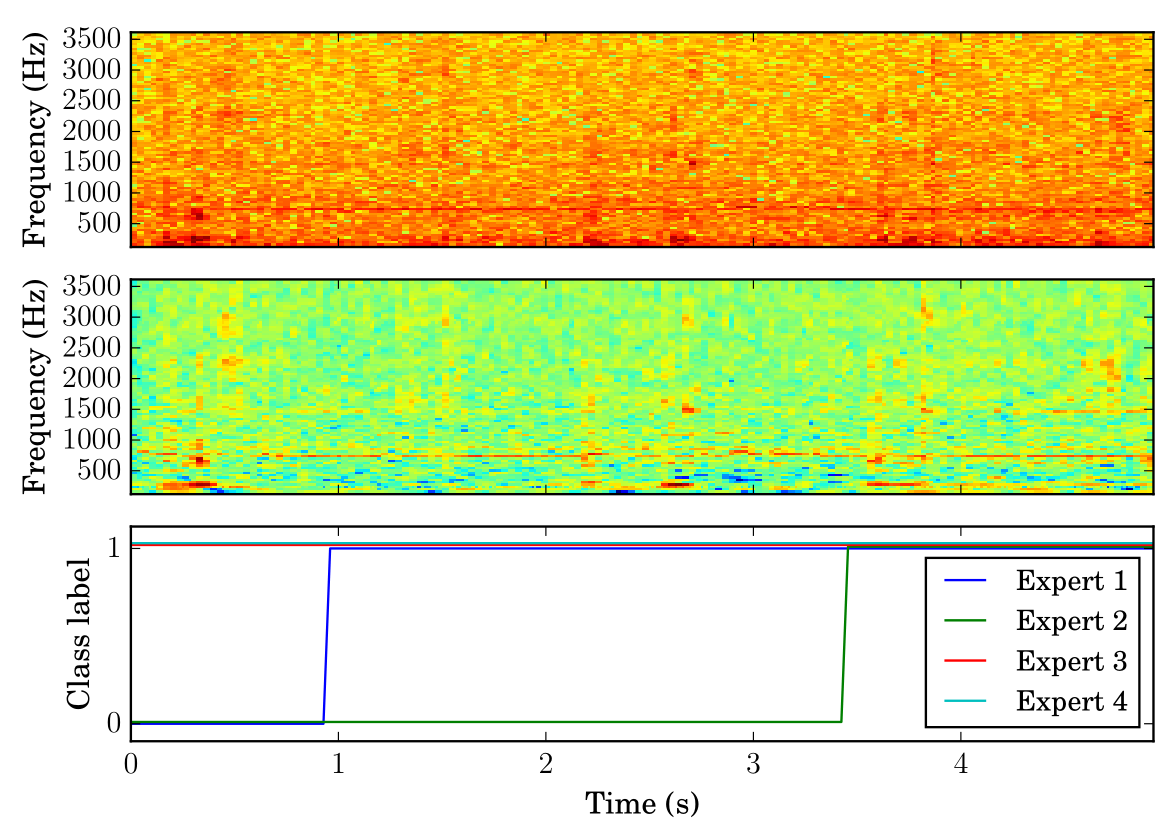
[图3：具有h1 = 256频率箱和小波尺度的信号的STFT（顶部）和小波（中间）表示。人类专家提供的相应变化类标签（底部）。小波表示显示在对应蚊子音调的水平恒定频率带中有更大对比度。]

6.2 参数交叉验证

在本节中，我们报告我们使用交叉验证估计的设计和参数考虑。可用的57个记录被分为37个训练和20个测试信号，为窗口宽度 $w_1 = 10$ 和 $w_1 = 1$ 样本创建大约6,000到60,000个训练样本。两个神经网络都以256的批次大小训练20个时期，根据验证准确率结合早停准则。

我们从CNN开始，注意信号的特征长度尺度决定切片宽度的选择。对于音乐摘录或鸟歌，捕获时间结构至关重要。这有利于采用更长的部分，允许在时域（沿x轴）有适当的卷积感受野。蚊子音调在时间上相对一致的频率，所以更短的切片可能提供更大的训练集而不失去每个部分的信息。因此，我们限制自己将训练数据分为320毫秒固定宽度样本（ $w_1 = 10$ ）。在选择要试用的滤波器宽度时，我们注意到频谱图样本在局部区域相关并将包含非局部谐波。局部性限于窄频带，以及通过时间（分别沿y和x轴）。考虑到这一点，我们得出表1的交叉验证网格和结果。

对于MLP，我们选择交叉验证最窄的训练样本宽度 $w_1 = 1$ ，以及CNN架构样本宽度 $w_1 = 10$ 形成列向量 $x_{train} \in \mathbb{R}^{h_1w_1 \times 1}$ 用于每个训练样本。然后我们估计表1给出的最优隐藏单元数。

传统分类器与表1中 $n, m$ 给出的PCA和RFE维数缩减交叉验证。所有传统分类器的最佳执行特征集是通过[13]中交叉验证递归特征消除提取的集合，超越每个分类器-特征对的所有PCA缩减。结果是我们表示为RFE88的特征集，它从跨越304维的十个原始特征中保留88维（ $F_{10} \in \mathbb{R}^{304}$ ）。

[表1：交叉验证结果。最优超参数以粗体给出。]

分类器	特征	交叉验证网格
CNN	STFT	$k \in {2, 3, 4, 5}, N_k \in {8, 16, 32}, N_d \in {16, 64, 128, 256}$
CNN	小波	$k \in {2, 3, 4, 5}, N_k \in {8, 16, 32}, N_d \in {16, 64, 128, 256}$
MLP	STFT	$w_1 \in {1, 10}, L \in {8, 256, 1028, 2056}, M \in {64, 512, 1024}$
MLP	小波	$w_1 \in {1, 10}, L \in {8, 256, 1028, 2056}, M \in {64, 512, 1024}$
NB, RF, SVM	$F_{10} \in \mathbb{R}^{304}$	PCA $\in \mathbb{R}^N, N \in 0.8n \times 304, n \in {0, 1, \ldots, 12}$ , RFE $\in \mathbb{R}^M, M \in 304 - 8m, m \in {0, 1, \ldots, 27, \ldots 35}$

7. 分类性能

性能指标在提取特征的分辨率下定义并在表2中呈现。我们强调最终目标是在智能手机或嵌入式设备上进行现场工作部署。设备将处于恒定监听模式，主要在由信号检测启动的数据写入模式期间消耗功率。对于此应用，高真负率（TNR）非常理想，因为防止假阳性检测导致关键的电池电源节约。考虑到这一点，我们突出四个关键结果。

首先，在小波特征上训练神经网络相比在STFT特征上训练显示一致的相对改进。我们将改进的接收器操作特征曲线（ROC）面积归因于网络产生每个预测的更好不确定性估计。结果，检测器输出 $0 \leq y_i \leq 1$ 的更大范围被利用。这最好通过ROC曲线平滑度的对比以及图4中分类器测试输出可见的预测分散来表示。

其次，卷积层的添加相比MLP在每个性能指标上提供显著增加。因此，省略CNN的特定位置约束降低了性能。

第三，在小波特征上训练的CNN能够进行F1分数、精确率-召回率（PR）和ROC面积的分类，远远超过使用传统分类器获得的结果。这尽管使用了详细的手工调整特征选择方案，该方案交叉验证PCA和RFE以提取显著特征。通过同时比较在STFT特征上条件化的较低实现CNN，我们注意到特征表示和架构都为检测过程增加了关键价值。

最后，对以小波特征为条件的CNN预测进行中值滤波大大提升了性能指标，允许我们的算法超越人类专家。通过使用表示人类标记大约发生的平滑度的中值滤波核（1秒），我们能够与人类专家标记比较性能。由于人类标签提供为绝对（要么 $y_i = 1,y_i = 0$ ），不正确标签对ROC和精确率-召回率曲线面积造成大的惩罚。这导致CNN-小波网络的远超ROC面积0.970，相比三个人类专家分别的0.873、0.901和0.874。然而，即使原始准确性也是可比的，如我们滤波算法和最佳手工标签尝试的近似相同F1分数所示。进一步的算法改进很容易获得（例如分类器聚合和时间池化），但超出了本文的范围。

[表2：总结分类指标。指标从测试数据的单次运行评估，跟随训练数据集上特征和超参数的10折交叉验证。]

分类器	特征	F1分数	TPR	TNR	ROC面积	PR面积
MLP	STFT	0.751	0.65	0.96	0.858	0.830
MLP	小波	0.745	0.63	0.97	0.921	0.875
CNN	STFT	0.779	0.69	0.96	0.871	0.853
CNN	小波	0.817	0.73	0.97	0.952	0.909
朴素贝叶斯	STFT	0.521	0.65	0.74	0.743	0.600
朴素贝叶斯	RFE88	0.484	0.51	0.83	0.732	0.414
随机森林	STFT	0.674	0.69	0.89	0.896	0.733
随机森林	RFE88	0.710	0.68	0.93	0.920	0.800
SVM	STFT	0.685	0.83	0.81	0.902	0.775
SVM	RFE88	0.745	0.73	0.93	0.928	0.831
CNN，中值滤波	小波	0.854	0.78	0.98	0.970	0.939
专家1	N/A	0.819	0.89	0.85	0.873	0.843
专家2	N/A	0.856	0.92	0.88	0.901	0.873
专家3	N/A	0.852	0.77	0.98	0.874	0.901

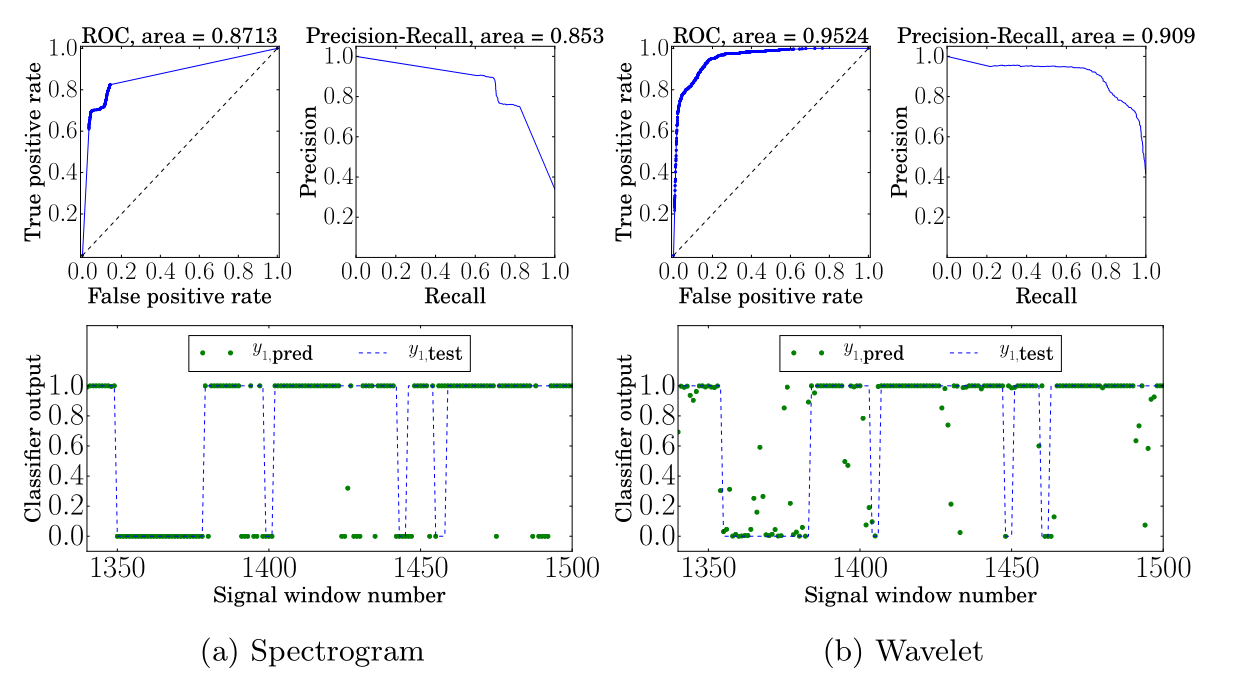
[图4：测试数据上的ROC、精确率-召回率和分类器输出，用于4a：具有256个傅里叶系数的频谱图和4b：具有256个尺度的小波。信号窗口范围的目标预测由蓝色虚线给出，实际预测由绿色点表示。每个预测在w1 = 10样本上生成——320毫秒的窗口。]

7.1 可视化判别能力

在缺乏数据标签的情况下，可视化可能是理解神经网络如何获得判别能力的关键。为了确保信号的特征已被成功学习，我们计算最大激活网络单元样本的频谱 $X_i(f)$ 。我们收集蚊子类 $\hat{y}_1$ 和非蚊子类 $\hat{y}_0$ 的最高N个预测。高分测试数据形成张量 $X_{i,test} \in \mathbb{R}^{N \times 256 \times 10},i = {0, 1}$ ，这是N个频谱图补丁的级联。然后通过取补丁和单个列的集合平均来计算频谱：

$x_{i,test}(f) = \frac{1}{10} \frac{1}{N} \sum_{j=1}^{10} \sum_{k=1}^{N} X_{ijk}, \quad \text{where } X_{ijk} \in \mathbb{R}^{256}$

类似地，我们从 $N_s$ 标记训练样本为两个类计算频谱 $x_{i,train}(f)$ 。我们使我们的频谱零均值和单位方差，以便在每个类的高分测试频谱 $x_{i,test}(f)$ 和它们来自训练集的参考 $x_{i,train}(f)$ 之间进行直接比较。蚊子类的结果测试频谱（ $x_1(f)$ ，图5）显示在650 Hz附近有明显的频率峰值。这个峰值清楚地匹配蚊子的可听频率，确认网络基于真实信号的学习特征进行预测。对于噪声频谱（ $x_0(f)$ ）也是如此，它由300 Hz附近的组件主导。学习和标记频谱之间的不匹配会向用户发出警告标志，暗示网络可能例如学习检测用于数据收集的麦克风的噪声轮廓而不是蚊子飞行音调。

[图片位置：频谱分析图 - 图5：测试数据集上前10%预测输出的标准化小波系数幅度与每个小波尺度的中心频率图。学习的频谱xi,test(f)对于最高N分数与标记类样本xi,train(f)的频率特征密切匹配。]

8. 结论

本文提出了一种在现实世界、数据稀缺情景中对自由飞行蚊子进行声学分类的新方法。我们表明卷积神经网络超越了该领域常用的通用分类器，如随机森林和支持向量机。在原始小波频谱图上训练的神经网络也超越了传统手工特征提取技术，超过任何替代特征-算法对的组合。此外，我们得出结论，添加卷积层导致相对于具有傅里叶和小波表示的非卷积神经网络的性能提升。通过进一步添加滚动中值滤波，该方法能够改善人类专家标记。

此外，我们的通用特征变换允许我们通过反向传播网络做出的预测来可视化学习的类表示。因此我们验证网络正确推断蚊子的频率特征，而不是记录的特殊性，如麦克风噪声轮廓。未来工作将概括我们的模型到多个类，如个别蚊子种类，并在物理设备中部署我们的算法以允许大规模数据收集。

参考文献

[1] Ai, O.C., Hariharan, M., Yaacob, S., Chee, L.S.: Classification of speech dysfluencies with MFCC and LPCC features. Expert Systems with Applications 39(2), 2157–2165 (2012)

[2] Akay, M.: Time Frequency and Wavelets in Biomedical Signal Processing. IEEE press series in Biomedical Engineering (1998)

[3] Alphey, L., Benedict, M., Bellini, R., Clark, G.G., Dame, D.A., Service, M.W., Dobson, S.L.: Sterile-insect methods for control of mosquito-borne diseases: an analysis. Vector-Borne and Zoonotic Diseases 10(3), 295–311 (2010)

[4] Bhatt, S., et al.: The effect of malaria control on Plasmodium falciparum in Africa between 2000 and 2015. Nature 526(7572), 207–211 (2015)

[5] Bhattacharya, S., Basu, P.: The southern house mosquito, Culex quinquefasciatus: profile of a smart vector. J Entomol Zoo Stud 4, 73–81 (2016)

[6] Chen, Y., Why, A., Batista, G., Mafra-Neto, A., Keogh, E.: Flying insect classification with inexpensive sensors. Journal of insect behavior 27(5), 657–677 (2014)

[7] Chesmore, E., Ohya, E.: Automated identification of field-recorded songs of four British grasshoppers using bioacoustic signal recognition. Bulletin of Entomological Research 94(04), 319–330 (2004)

[8] Clemins, P.J., Johnson, M.T.: Automatic type classification and speaker identification of African elephant vocalizations (2002)

[9] Daubechies, I., Lu, J., Wu, H.T.: Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Applied and computational harmonic analysis 30(2), 243–261 (2011)

[10] Giannakopoulos, T.: pyAudioAnalysis: An open-source Python library for audio signal analysis. PloS one 10(12), e0144610 (2015)

[其余参考文献略...]