基于混合注意力网络和深度信念网络的鲁棒视频水印技术基础理论深度解析

1. 引言

随着数字媒体技术的迅猛发展和互联网的普及，视频内容的创作、传播和分享变得前所未有的便捷。然而，这种便利性也带来了严重的版权保护挑战。数字视频的易复制性使得盗版和非法传播成为困扰内容创作者和版权所有者的重大问题。传统的加密技术虽然能够在一定程度上保护数字内容，但一旦内容被解密，就失去了进一步的保护能力。在这种背景下，数字水印技术作为一种新兴的版权保护手段应运而生，它能够将版权信息直接嵌入到数字媒体内容中，实现对数字内容的持久性保护。

数字水印技术的核心思想是在不影响原始内容感知质量的前提下，将特定的标识信息（水印）隐藏在数字媒体中。这些水印信息在正常的观看或使用过程中是不可见或不可感知的，但可以通过特定的算法和密钥提取出来，从而实现对数字内容的版权认证、完整性验证和来源追溯。与传统的版权保护方法相比，数字水印技术具有隐蔽性强、鲁棒性好、容量大等优势，已经成为数字版权保护领域的重要技术手段。

视频水印作为数字水印技术的重要分支，面临着比图像水印更为复杂的技术挑战。视频数据不仅具有空间维度的特征，还包含时间维度的信息，这使得视频水印需要在空域、频域和时域等多个维度上进行考虑。同时，视频在传输和存储过程中可能遭受各种有意或无意的攻击，如压缩、噪声添加、几何变换、帧操作等，这要求视频水印算法必须具备足够的鲁棒性来抵抗这些攻击。

近年来，深度学习技术的快速发展为数字水印领域带来了新的机遇和挑战。基于深度学习的水印方法能够自动学习数据的深层特征表示，实现更加智能和自适应的水印嵌入和提取策略。特别是注意力机制的引入，使得水印算法能够动态地关注视频内容中最重要的区域，从而在保证不可感知性的同时提高鲁棒性。

论文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》提出了一种创新的视频水印方法，该方法巧妙地融合了多种先进技术，包括注意力机制（Attention Mechanism）、深度信念网络（Deep Belief Network）、四元数曲波变换（Quaternion Curvelet Transform）以及黄金分割斐波那契树优化算法（Golden Section Fibonacci Tree Optimization）。这种多技术融合的方法在视频水印的不可感知性和鲁棒性之间实现了良好的平衡，为视频版权保护提供了新的技术路径。

2. 数字水印技术基础理论

2.1 数字水印的基本概念与分类

数字水印技术起源于物理世界中的纸质水印概念，但其内涵和外延都得到了极大的扩展。从技术角度来看，数字水印是一种信息隐藏技术，它将特定的数字信号（水印）嵌入到数字媒体载体中，使得水印信息与载体内容紧密结合，难以被分离或篡改。这种嵌入过程需要满足两个基本要求：一是不可感知性（Imperceptibility），即水印的嵌入不应该明显影响载体的感知质量；二是鲁棒性（Robustness），即水印信息应该能够抵抗各种可能的攻击和处理操作。

根据水印嵌入的域空间不同，数字水印技术可以分为空域水印和变换域水印两大类。空域水印直接在像素层面进行操作，通过修改图像或视频帧的像素值来嵌入水印信息。最典型的空域水印方法是最低有效位（Least Significant Bit, LSB）方法，它将水印信息替换载体图像的最低有效位。LSB方法的优点是实现简单、嵌入容量大，但缺点是鲁棒性较差，容易受到各种信号处理操作的影响。另一种常见的空域方法是叠加法，它将水印信号与载体信号直接相加，数学表达式为：

$I_w(x,y) = I(x,y) + \alpha \cdot W(x,y)$

其中 $I(x,y)$ 表示原始载体图像， $W(x,y)$ 表示水印信号， $\alpha$ 表示嵌入强度因子， $I_w(x,y)$ 表示嵌入水印后的图像。

变换域水印则是在频域中进行水印嵌入，它首先将载体信号通过某种数学变换转换到频域，然后在变换系数中嵌入水印信息，最后通过逆变换得到嵌入水印的载体信号。常用的变换包括离散余弦变换（DCT）、离散小波变换（DWT）、离散傅里叶变换（DFT）等。变换域水印的主要优势在于其良好的鲁棒性，因为频域系数通常对常见的信号处理操作（如压缩、滤波等）具有更强的抗干扰能力。例如，在DCT域中的水印嵌入可以表示为：

$C_w(u,v) = C(u,v) + \alpha \cdot W(u,v)$

其中 $C(u,v)$ 表示原始DCT系数， $W(u,v)$ 表示水印信号在DCT域的表示， $C_w(u,v)$ 表示嵌入水印后的DCT系数。

2.2 视频水印的特殊挑战

与静态图像相比，视频水印面临着更多的技术挑战。首先，视频具有时间维度，这使得水印算法需要考虑帧间的相关性和时间一致性。视频中相邻帧之间往往存在很强的相关性，这种相关性既可以被利用来提高水印的鲁棒性，也可能成为攻击者利用的弱点。其次，视频数据量庞大，对算法的计算效率提出了更高的要求。一个典型的高清视频文件可能包含数十万帧图像，如果对每一帧都进行复杂的水印处理，将会带来巨大的计算开销。

视频在传输和存储过程中还可能遭受各种特有的攻击，包括时域攻击和空域攻击。时域攻击主要针对视频的时间特性，如帧丢弃（Frame Dropping）、帧重排（Frame Reordering）、帧插入（Frame Insertion）等。这些攻击会破坏视频的时间结构，可能导致基于时间相关性的水印信息丢失。空域攻击则包括传统的图像处理攻击，如噪声添加、滤波、几何变换等，以及视频特有的压缩攻击。视频压缩是视频处理中最常见的操作，不同的压缩标准（如H.264、H.265等）采用不同的压缩算法，这些算法可能会显著影响嵌入的水印信息。

为了应对这些挑战，视频水印算法通常采用关键帧（Key Frame）选择策略，即只在视频的关键帧中嵌入水印信息。关键帧的选择需要考虑多个因素，包括帧的重要性、视觉显著性、运动信息等。数学上，关键帧的选择可以建模为一个优化问题：

$\arg\max_{F \subset {f_1, f_2, ..., f_N}} \sum_{f_i \in F} \text{Importance}(f_i)$

其中 ${f_1, f_2, ..., f_N}$ 表示视频中的所有帧，F表示选择的关键帧集合， $\text{Importance}(f_i)$ 表示第 $i$ 帧的重要性度量。

2.3 水印系统的性能评价指标

数字水印系统的性能通常通过多个指标来评价，这些指标反映了水印算法在不可感知性、鲁棒性、安全性等方面的表现。不可感知性是衡量水印嵌入对载体质量影响程度的指标，常用的客观评价指标包括峰值信噪比（Peak Signal-to-Noise Ratio, PSNR）和结构相似性指数（Structural Similarity Index, SSIM）。PSNR的计算公式为：

$\text{PSNR} = 10 \log_{10} \frac{\text{MAX}^2}{\text{MSE}}$

其中MAX表示图像可能的最大像素值，MSE表示均方误差：

$\text{MSE} = \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} [I(i,j) - I_w(i,j)]^2$

SSIM指标考虑了人眼视觉系统的特性，通过比较亮度、对比度和结构信息来评价图像质量：

$\text{SSIM}(x,y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)}$

其中 $\mu_x,\mu_y$ 分别表示图像x和y的均值， $\sigma_x^2,\sigma_y^2$ 分别表示方差， $\sigma_{xy}$ 表示协方差， $c_1,c_2$ 为常数。

鲁棒性评价主要关注水印在各种攻击下的生存能力，常用指标包括归一化相关系数（Normalized Correlation Coefficient, NCC）和误码率（Bit Error Rate, BER）。NCC用于衡量提取水印与原始水印之间的相似度：

$\text{NCC} = \frac{\sum_{i=1}^{N} W_i \cdot W'i}{\sqrt{\sum{i=1}^{N} W_i^2} \sqrt{\sum_{i=1}^{N} W'^2_i}}$

其中 $W_i$ 表示原始水印的第i个元素， $W'_i$ 表示提取水印的第i个元素。BER则计算错误提取的比特数占总比特数的比例：

3. 注意力机制的基础原理

3.1 注意力机制的生物学启发与数学基础

注意力机制源于对人类认知过程的模拟，特别是人类视觉注意力系统的工作原理。在日常生活中，人类面对复杂的视觉场景时，并不会同时关注所有的细节，而是会选择性地将注意力集中在最重要或最相关的信息上。这种选择性注意的能力使得人类能够在有限的认知资源下高效地处理大量信息。心理学研究表明，人类的注意力机制包括自下而上（bottom-up）和自上而下（top-down）两种模式。自下而上的注意力由刺激的显著性驱动，而自上而下的注意力则由任务目标和先验知识引导。

在深度学习中，注意力机制的数学基础可以追溯到信息论和概率论。从信息论的角度来看，注意力机制可以理解为一种信息选择和过滤机制，它通过分配不同的权重来突出重要信息，抑制不相关信息。数学上，注意力机制可以表示为一个加权平均的过程：

$\text{Attention}(Q, K, V) = \sum_{i=1}^{n} \alpha_i v_i$

其中Q表示查询（Query），K表示键（Key），V表示值（Value）， $\alpha_i$ 表示注意力权重， $v_i$ 表示第i个值向量。注意力权重 $\alpha_i$ 的计算通常涉及查询和键之间的相似度计算：

$\alpha_i = \frac{\exp(f(q, k_i))}{\sum_{j=1}^{n} \exp(f(q, k_j))}$

其中 $f(q, k_i)$ 表示查询q与第i个键 $k_i$ 之间的相似度函数，常用的相似度函数包括点积、加性注意力、多层感知机等。

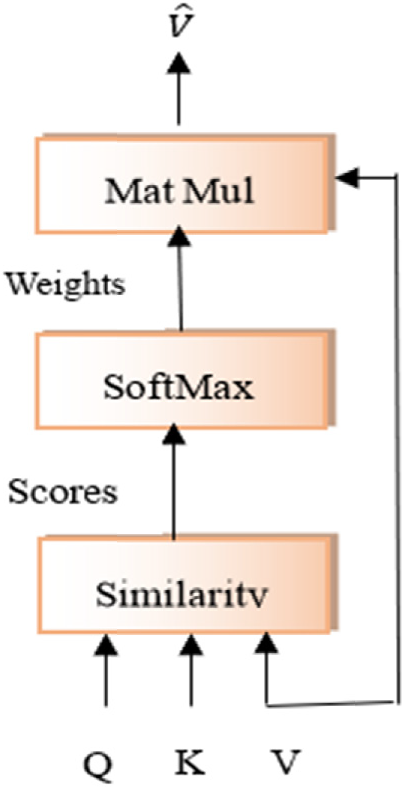
3.2 Scaled Dot-Product Attention的数学原理

Scaled Dot-Product Attention是最常用的注意力计算方法，它使用向量点积来计算查询和键之间的相似度。点积操作的几何意义是计算两个向量之间的夹角余弦，当两个向量方向相似时，点积值较大，表示较高的相关性。Scaled Dot-Product Attention的完整计算公式为：

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

其中 $d_k$ 表示键向量的维度，除以 $\sqrt{d_k}$ 的目的是进行缩放，防止点积结果过大导致softmax函数进入饱和区域。这种缩放的必要性可以从统计学角度来理解：假设Q和K的元素是独立的随机变量，均值为0，方差为1，那么它们的点积的方差为 $d_k$ 。通过除以 $\sqrt{d_k}$ ，可以使得缩放后的点积具有单位方差，从而稳定训练过程。