本文探讨了二叉搜索树在数据库存储引擎中的角色。二叉搜索树是一种有序数据结构，适用于高效的键值查找。然而，由于其可能的不平衡性导致的查询效率下降，平衡二叉树如AVL树变得重要。此外，二叉树在磁盘存储时面临局部性和扇出数问题，导致其不适合作为磁盘上的数据结构。为了解决这些问题，高扇出和低高度的树结构如B树成为了理想选择，它们能有效减少磁盘访问并提高性能。
B树是数据库存储引擎使用的最多的存储结构之一。许多开源数据库系统也都大量使B用树作为存储结构，多年来已经证明它们能够胜任大多数使用场景。
早在1971年鲁道夫·拜尔(Rudolph Bayer)和爱德华·M·麦克立特(Edward M. McCreight)就提出了B树这种数据结构，并受到广泛的应用。到1979年，B树已经发展出了许多变种形式。
在深入讨论B树之前，让我们首先讨论一下传统搜索树，例如，二叉搜索树、2-3树和AVL树。
二叉搜索树（Binary Search Tree）
二叉搜索树(BST)是一种有序的内存数据结构，用于高效的键值查找。二叉搜索树由多个节点组成。每个树节点由一个键、一个与此键关联的值和两个子指针构成。二叉搜索树从一个称为根节点的节点开始，且一棵树只有一根节点。图2-1展示了一棵二叉搜索树。
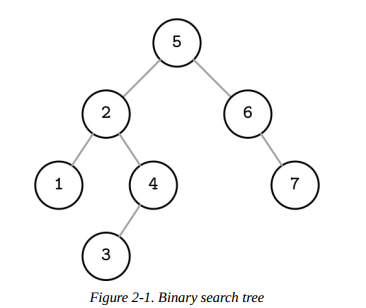
在二叉搜索树中搜索空间被每个节点划分成左子树和右子树。如图2-2,一个节点的键值总是大于它左子树所有节点的键值，同时总是小于它右子树所有节点的键值。
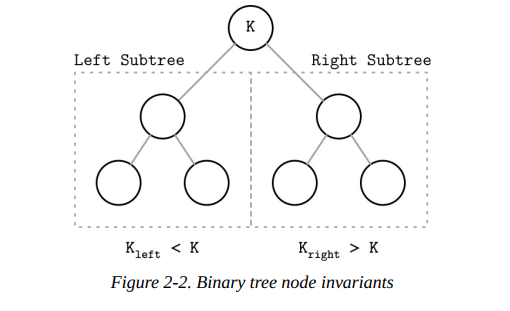
从树的根节点沿左子树指针向下到达叶子层(没有子节点的节点)，就可以找到树中包含最小键值的节点。类似地，沿右子树指针向下就可以找到树中包含最大键值的节点。通常，键值可以保存在树中的所有节点中，因此如果从根节点开始搜索，在到达树的最底层之前搜索键就可能被找的。
平衡二叉树
如果随机的插入数据到二叉树中，二叉树就可能处于一种不平衡的状态，即它的一个分支比另一个分支长。图2-3（b）展示了最差的这种情况，这时它更像一个链表。查询的时间复杂度也是和链表一样是线性的，而不像
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
