深入理解数据库之存储存引擎（B树）

二叉搜索树不适合应用到磁盘上，因为它的扇出数较低并且平衡时需要大量的节点重定位和指针更新。B树通过增加每个节点存储项的数量(高扇出)和减少频繁的平衡操作来解决这些问题。下面我们将讨论了B树的内部结构，B树的查找、插入和删除操作算法概要，以及用于保持B树平衡的拆分和合并操作。

B树实际上是平衡二叉树的扩展，不同之处在于B树具有更大的扇出数（即更多的子节点）和更低的树高。前文讨论二叉树时节点以圆形表示，而B树节点通常以矩形表示，当然二叉树也可以使用矩形来表示。图2-7使用矩形的方式表示二叉树，2-3树和B树，从中我们可以看出它们之间的相似性和差异性。

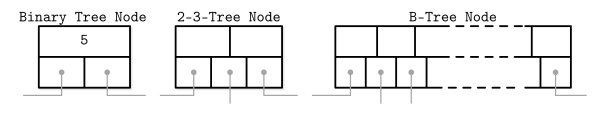
B树的节点也是有序排列的，因此B树可以像二叉搜索树一样进行节点查找。这也就是说B树查找节点的时间复杂度是对数的，通过32次比较就能从包含40亿个节点的B树中找到某个键。

对于磁盘数据结构，如果每次比较都要经过磁盘扇区定位，这样的性能显然是不能接受的。但是每个B树节点存储几十甚至上百个条目，这就避免了每次比较都需要定位新的磁盘扇区，仅仅在进入B树下一层的时候才需要重定位加载新扇区。后面我们会更加详细的讨论查询算法的细节。

B树上可以非常高效的查询单个数据或者是查询某个范围内的数据。在查询语言里（如SQL），查询某个数据通常表示为等于（=），而查询某个范围数据通常表示为比较（<, >, ≤和≥）。

B树的层次结构

B树由多个节点构成，每个节点又包含N个键和N+1个指向子节点的指针。从逻辑上节点可以分成3类：

根节点(Root Node)： 根节点没有父节点，位于树的最顶部；

叶子节点(Leaf Nodes)： 树的最底层节点，而且没有任何子节点。

内部节点(Internal Nodes): 所有连接根节点和叶子节点的节