数据库索引数据结构-二叉查找树

1、定义：

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
（4）没有键值相等的节点。

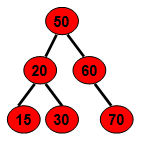
如上图所示：50的左子树不为空，则50的左子树上所有结点20、15、30都是小于50的。

2、查找

1、任何一个数据的查找过程都需要从根结点出发，沿某一个路径朝叶子结点前进。因此查找中数据比较次数与树的形态密切相关。
2、当树中每个结点左右子树高度大致相同时，树高为logN。则平均查找长度与logN成正比，查找的平均时间复杂度在O(logN)数量级上。
3、当先后插入的关键字有序时，BST退化成单支树结构。此时树高n。平均查找长度为(n+1)/2，查找的平均时间复杂度在O(N)数量级上。

3、插入与删除

1、新结点插入到树的叶子上，完全不需要改变树中原有结点的组织结构。插入一个结点的代价与查找一个不存在的数据的代价完全相同
2、当删除一个结点P，首先需要定位到这个结点P，这个过程需要一个查找的代价。然后稍微改变一下树的形态。如果被删除结点的左、右子树只有一个存在，则改变形态的代价仅为O(1)。如果被删除结点的左、右子树均存在，只需要将当P的左孩子的右孩子的右孩子的…的右叶子结点与P互换，在改变一些左右子树即可。因此删除操作的时间复杂度最大不会超过O(logN)。

4、小结

1、查找最好时间复杂度O(logN)，最坏时间复杂度O(N)。
2、插入删除操作算法简单，时间复杂度与查找差不多。