生物信息基础 学习笔记（1）

生物信息基础  学习笔记 (1)——穷举搜索

部分酶切问题：

 

已知多重集，求原来的集合 X，可以有多个 。

例子：X = { 0 ， 2 ， 4 ， 7 ，10 }，则 = { 2 , 2 , 3 , 3 , 4 , 5 , 6 , 7, 8 , 10 }

不同的 X 可能产生相同的  , 这样的 X 称为同效集。

现在已知 ，要求所有的 X 。

不实用的限制酶切作图算法

课本上给出了暴力搜索的伪代码。

整体思路，就是先找出中最大的元素，设为 width , width 就是原集合 X 中最大元素，因为 X 中一定含有 0，因为有一个起点，起点和自己的距离是 0，那么 中就存在 ——X 的最大元素- 0 = 的最大元素。

然后从 0 到 M 的数字中，选出所有包含 n-2 个数（因为 0 和width 已经选好了）的集合，求出相应的  , 和实际的  = L 对比，如果可以得出一样的，说明这个 X 是符合要求的。

但是，M-1 个数中要选出 n-2 个点，复杂度很高，再加上生成和匹配L的过程，比较耗时。

穷举搜索一定可以找出解，因为遍历了所有的解空间，缺点就是复杂度高，实际应用效果不好。

实用的限制酶切图解法

穷举算法，慢在搜索了很多无用的空间，如果适当剪枝，可以减少大量的无用计算。

书本上给出了更好的算法： L 代表已知的 

 

关键就在：每次检验如果加入 y, y 和现有 X 构成的差集（都是正数），在 L 中都出现过了，说明——y 和 X 的差集可以构成中的某些元素；但是如果差集中有的元素在 L 中没出现过，说明 X 中不存在 y 。然后把 L 中这些元素删除，删除是为了防止对后面的搜索造成干扰。

然后继续搜索，

然后，在 X 中删除 y , 回溯搜索另一边 width - y 和 X 的差集。

还要检验 width - y 的原因是，差集可能有和 0 产生的 y - 0 = y，也可能有和 width 产生的 width - y 。举个例子，width = 10 , X 中一定含有 0  和 width = 10 ， 也就是 L 中含有 7 ， 这个 7 可能是 7 和 X 的0的差，也可能是 3 和 X 的 10 之差。

尝试写了一下C++实现，我用了 multiset 来储存多重集。

不过书本上给出的代码有点歧义

这里的顺序，应该是先在 L 中删除  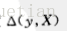 ，再把 y 添加到 X ，因为如果先添加 X , 在后面删除 就会多删除一个 0 ( y - y = 0 ) 。要先删除，再添加。

回溯的顺序，书上的是没歧义的 。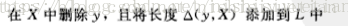

#include <bits/stdc++.h>
using namespace std ;
int n , size , width , cost ;
multiset<int> L ;
multiset<int> X ;

// 打印最后得出的解集合 X 
void display ( const multiset<int> &One ) {
	multiset<int>::iterator it = One.begin () ;
	for ( ; it != One.end () ; ++it )
		cout << *it << "  " ;
	cout << endl ;
}

// 如果把 y 加入到 X, y 和 X 构成的差集是不是都在 L 出现过了
int Judge ( const int y ) {
	multiset<int>::iterator it = X.begin () ;
	for ( ; it != X.end () ; ++it ) 
		if ( L.count ( abs ( y - *it ) ) == 0 ) 
			return 0 ;
	return 1 ;
}

// L 中删除 y 和 X 构成的差集
void Erase ( multiset<int> &L , const int y ) {
	multiset<int>::iterator it = X.begin () ;
	for ( ; it != X.end () ; ++it ) 
		L.erase ( L.lower_bound ( abs ( y - *it ) ) ) ;
}

// L 加上 y 和 X 构成的差集
void Add ( multiset<int> &L , const int y ) {
	multiset<int>::iterator it = X.begin () ;
	for ( ; it != X.end () ; ++it )
		L.insert ( abs ( y - *it ) ) ;
}

void Place () {
	// if L 是空集
	if ( L.empty () ) {                        // X.size() == (int)sqrt( 2 * n ) + 1 
		display ( X ) ; return ;
	}
	// 取出 L 中的最大元素
	multiset<int>::reverse_iterator it = L.rbegin () ;
	int y = (*it) ;
	// 如果 y 和 X 构成的差集, 其元素都在 L 中出现了
	if ( Judge ( y ) ) {
		// L 中删除 y 和 X 构成的差集, 再把 y 加入到 X 集合中
		Erase ( L , y ) , X.insert ( y ) ;
		Place () ;
		// X 中先删除 y, 然后 L 加上 y 和 X 构成的差集, 回溯
		X.erase ( y ) , Add ( L , y ) ;
	}
	// 如果 width - y 和 x 构成的差集, 其元素都在 L 中出现了
	if ( Judge ( width - y ) ) {
		Erase ( L , width - y ) , X.insert ( width - y ) ;
		Place () ;
		X.erase ( width - y ) , Add ( L , width - y ) ;
	}
}

// 根据 L 推导出原来的 X 集合
inline void Partial_Digest () {
	multiset<int>::reverse_iterator it = L.rbegin () ;
	width = *it ;             // 先取出最大长度
	L.erase ( *it ) ;        
	X.insert ( 0 ) , X.insert ( width ) ; // 初始化 X = { 0 , width }
	Place () ;
}

int main () {
	scanf ( "%d" , &n ) ;
	for ( int i = 1 ; i <= n ; ++i )
		scanf ( "%d" , &cost ) , 
	    L.insert ( cost ) ;
	Partial_Digest () ;
	return 0 ;
}

还没解决的问题：

 

1. 会搜索出重复解，我还没找到高效的检测一个序列重复的算法。

2. 我用的是 multiset, 和有序数组在一些操作上慢了 logn 倍，但是 multiset 使用方便。如果使用有序数组来存储集合，在找最大元素上O(1), 删除也是 O(1) 。

3. 虽然算法优化了，但依旧是指数级的复杂度。